数据结构与算法8—二叉树的遍历

二叉树遍历的几种方法

 

存储结构：

 

typedef char ElemType;
typedef struct BiTNode{
  ElemType data;
  struct BiTNode *lchild,*rchild;
}BiTNode;

 

 

遍历

树的遍历顺序是相对父结点来说的。

先序遍历：

先访问根结点,然后分别先序遍历左子树、右子树。

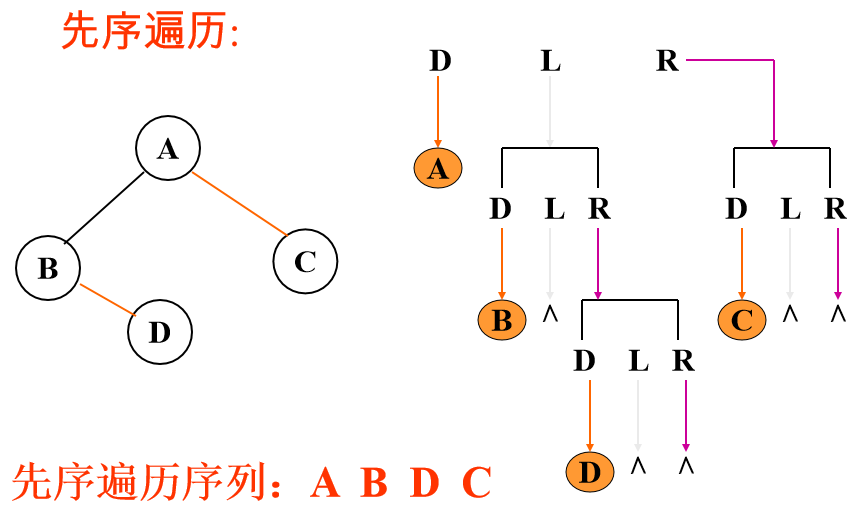
递归先序：

void PreOrderTraverse(BiTree bt)
{ /* 最简单的Visit函数：Visit(ElemType  e){printf(e);}*/
    if(bt){
        Visit(bt->data);
        PreOrderTraverse(bt->lchild);
        PreOrderTraverse(bt->rchild);
    }
}

非递归先序：

1. p=根结点地址，初始化栈

2. while(p!=NULL || 栈不空)

        while(p!=NULL ) 访问p, p入栈, p=p->lchild

        若栈不空，出栈p，p=p->rchild

void inorder_fdg(BiTNode *bt) /*非递归先序遍历*/
{   int top=0;
    BiTNode *p,*s[20];   p=bt;
    while(p!=NULL||top>0) {
       while(p!=NULL){   
           printf("%c ",p->data);   // 先序遍历
           s[top++]=p; p=p->lchild;
       }
       if(top>0)
       {   p=s[--top];
           //printf("%c ",p->data); // 中序遍历
           p=p->rchild;
       }
    }
}

 

中序遍历：

先中序遍历左子树，然后访问根结点，最后中序遍历右子树。

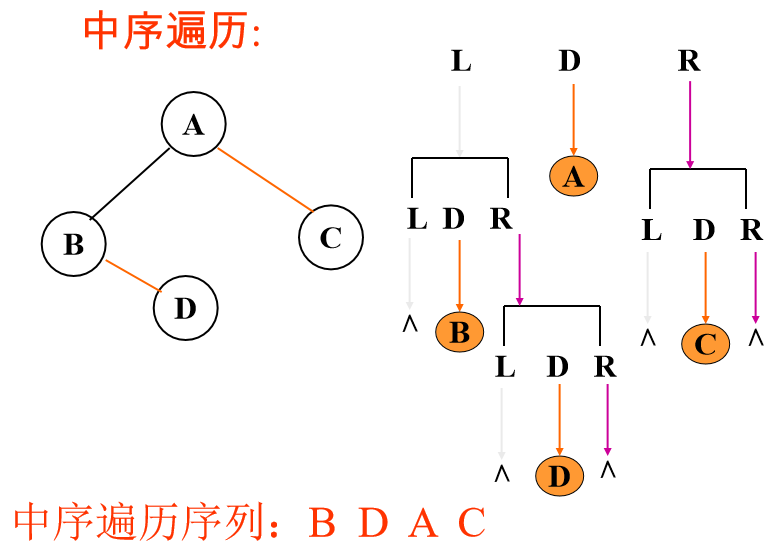
void InOrderTraverse(BiTree bt)
{ 
    if(bt){
        PreOrderTraverse(bt->lchild);
        Visit(bt->data);
        PreOrderTraverse(bt->rchild);
    }
}

 

后序遍历：

先后序遍历左、右子树，然后访问根结点。

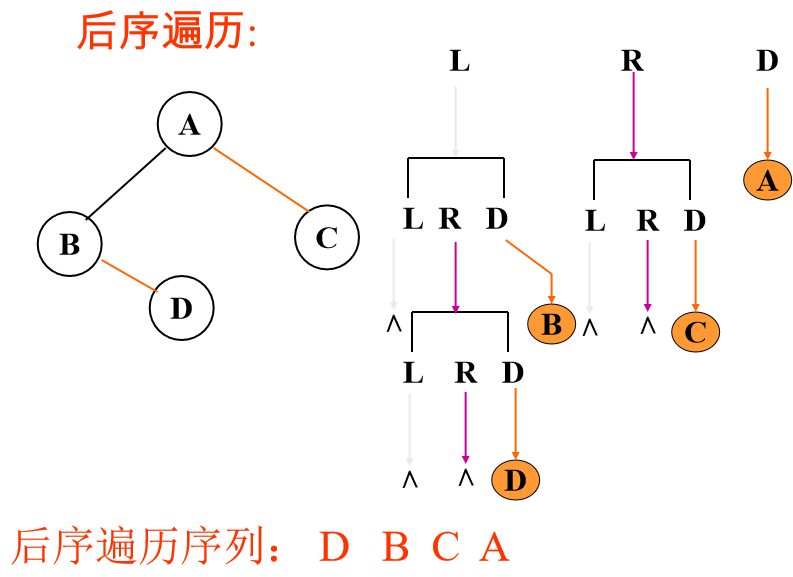
void InOrderTraverse(BiTree bt)
{ 
    if(bt){
        PreOrderTraverse(bt->lchild);
        PreOrderTraverse(bt->rchild);
        Visit(bt->data);
    }
}

 

按层次遍历：

从上到下、从左到右访问各结点。

可使用一个顺序存储的队列q[100],存放还没有处理的子树的根结点的地址。注意,队首和队尾指针分别指向队首结点和下次进队结点的存放位置。

• 首先把根节点入队。
• 然后访问队头的一个结点，再把该结点非空的左右子树入队。
• 如果队列不空，重复2)。

void lev_traverse(BiTNode* T)
{ /* 用队列实现层次遍历 */
  BiTNode *q[100],*p;
  int head,tail;  
  q[0]=T;head=0;tail=1;
  while(head<tail) { /* 当队列不空 */
    p=q[head++];
    printf("%c ",p->data);
     if(p->lchild!=NULL)
      q[tail++]=p->lchild;
     if(p->rchild!=NULL)
      q[tail++]=p->rchild;
  }
}

 

 

其他

先中后层的例子：

 

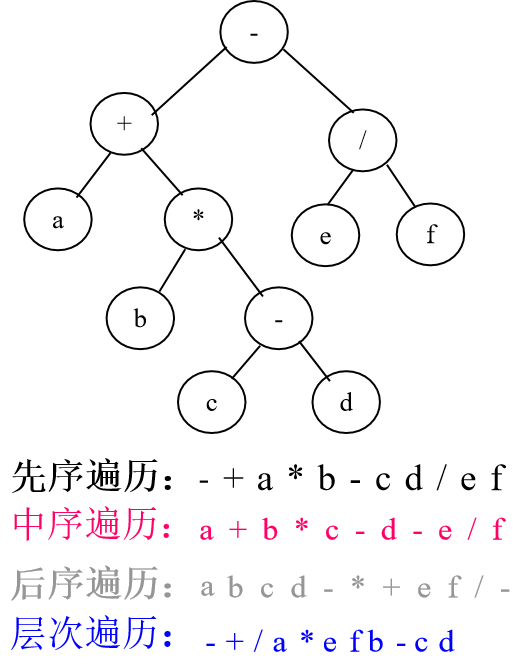
求二叉树的深度(后序遍历)

算法基本思想:

从二叉树深度的定义可知，二叉树的深度应为其左、右子树深度的最大值加1。

由此，需先分别求得左、右子树的深度，算法中“访问结点”的操作为：求得左、右子树深度的最大值，然后加 1 。

//计算二叉树的深度
int Depth(BiTNode *bt)
{
    int depth, depthLeft, depthRight;
    if (bt == NULL)
        depth = 0;
    else  {
        depthLeft = Depth(bt->lchild);
        depthRight = Depth(bt->rchild);
        depth = 1 + (depthLeft > depthRight ? depthLeft : depthRight);
    }
    return depth;
}