数据结构与算法3—栈

1. 栈的定义

• 栈，也叫堆栈，是最常用也是最重要的数据结构之一。
• 栈(Stack)是限定仅在表的一端进行插入或删除操作的线性表，通常称插入、删除的这一端为栈顶(Top)，另一端为栈底(Bottom)。当表中没有元素时称为空栈。
• 栈操作的特点：后进先出，先进后出。
• 因此，栈称为后进先出表（LIFO, Last In First Out）。

示意图：

 

2. 栈的基本运算

• 初始化栈InitStack(*S)
• 压栈Push(*S,x)    ——在栈顶插入元素
• 出栈Pop(*S,x)    ——在栈顶删除元素
• 取栈顶元素GetTop(S,x)
• 判栈空Empty(S)

栈的几种状态（最大长度MaxSize为4）：栈空、压栈、栈满、出栈

 

3. 栈的存储结构

栈有两种表示方法:顺序存储和链式存储

3.1 顺序栈

采用顺序存储结构的栈简称为顺序栈。是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素，同时附设整型变量top指示栈顶元素在顺序栈中的位置。

// 顺序栈数据类型的C语言描述如下：
#define MaxSize 100
typedef int DataType;
typedef struct {
          DataType data[MaxSize];
          int top;
}Stack;

// top:栈顶指针。取值范围为0～MaxSize-1。
// top==-1表示栈空，top==MaxSize-1表示栈满。 

// 初始化栈InitStack(S)
 int InitStack(Stack *S) 
 { 
     S->top=-1; 
     return 1;
 } 

// 压栈Push(S,x)
int Push(Stack *S,DataType x)
{
    if(S->top==MaxSize-1)
    {
         printf("\n Stack is full!"); 
        return 0;
    }
      S->top++;
      S->data[S->top]=x;
      return 1; 
}

// 判栈空EmptyStack(S)
int EmptyStack(Stack *S)
{ 
    return (S->top==-1?1:0);
}

// 出栈Pop(S,x)
int Pop(Stack *S,DataType *x)     
{ 
    if(EmptyStack(S))
    {   
          printf("\n Stack is free!"); 
           return 0;
    }
   *x=S->data[S->top];//记住要删除的元素值
       S->top--;
       return 1;
}

// 取栈顶元素GetTopStack(S)
DataType GetTop(STACK *S)   
{  
    DataType x;
    if(EmptyStack(S))
    {   
          printf("\n Stack is free!"); 
        exit(1);
    }
       x=S->data[S->top];
       return x;
}

3.1 链栈：栈的链式存储结构

链栈结构示意图：

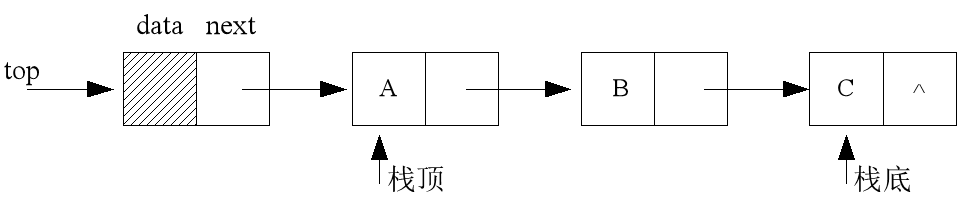
top栈顶指针，惟一的确定一个链栈。 链栈通常带有一个表头结点，所以top->next才指示栈顶元素。

//  链栈的C语言描述如下：

typedef struct node
{
    ElemType data;
    struct node *next;
}Stack;

Stack * InitStack() 
{
    Stack *top;
    top=(Stack *)malloc(sizeof(Stack));
    top->next=NULL;
    return top;
}
//进栈
int Push(Stack *top,Pos x) 
{
    Stack *s;
    s=(Stack *)malloc(sizeof(Stack));
    if(!s) //当s==NULL return 0
        return 0;
    s->data=x; 
    s->next=top->next; //新申请空间的指针域保存上一个结点的地址
    top->next=s;  //头指针域保存新结点地址
    return 1;
}
//判断栈空
int EmptyStack(Stack *top) 
{
    if(top->next==NULL)
        return 1;
    else
        return 0;
}
//出栈
int Pop(Stack *top,Pos *e) 
{
    Stack *s;
    if(EmptyStack(top))
        return 0;
    s=top->next;  //取第一个结点的地址
    *e=s->data;   //返第一结点数据
    top->next=s->next; //头结点指针域存第二结点地址
    free(s);
    return 1;
}

//取栈顶元素
int GetTopStack(Stack *top,Pos *e)
{
    Stack *s;
    if(EmptyStack(top))
        return 0;
    s=top->next;
    *e=s->data;
    return 1;
}