剑指Offer_编程题_重建二叉树

 

题目描述

链接：https://www.nowcoder.com/questionTerminal/8a19cbe657394eeaac2f6ea9b0f6fcf6?f=discussion
来源：牛客网

输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回

 

分析：先搞清楚二叉树遍历分为三种：前序、中序、后序

参考链接：https://blog.csdn.net/qq_42651904/article/details/90288715

　　　　　https://blog.csdn.net/qq_33243189/article/details/80222629

第二篇文章评论帮助理解的一句话：

下面是作者的原文 比如上图正常的一个满节点，A：根节点、B：左节点、C：右节点，前序顺序是ABC（根节点排最先，然后同级先左后右）；中序顺序是BAC(先左后根最后右）；后序顺序是BCA（先左后右最后根）。-----------而对于后面的任意一个节点处理方式也是相同的，比方说是中序遍历，那么到达该子节点，如果有左孩子，就先去对其左孩子进行操作，如果左孩子还有左孩子那就递归了

 

解题思路

链接：https://www.nowcoder.com/questionTerminal/8a19cbe657394eeaac2f6ea9b0f6fcf6?f=discussion
来源：牛客网

因为是树的结构，一般都是用递归来实现。

用数学归纳法的思想就是，假设最后一步，就是root的左右子树都已经重建好了，那么我只要考虑将root的左右子树安上去即可。

根据前序遍历的性质，第一个元素必然就是root，那么下面的工作就是如何确定root的左右子树的范围。

根据中序遍历的性质，root元素前面都是root的左子树，后面都是root的右子树。那么我们只要找到中序遍历中root的位置，就可以确定好左右子树的范围。

正如上面所说，只需要将确定的左右子树安到root上即可。递归要注意出口，假设最后只有一个元素了，那么就要返回。

 

链接：https://www.nowcoder.com/questionTerminal/8a19cbe657394eeaac2f6ea9b0f6fcf6?f=discussion
来源：牛客网

import java.util.Arrays;
public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
        //数组长度为0的时候要处理
        if(pre.length == 0){
            return null;
        }
 
        int rootVal = pre[0];
 
        //数组长度仅为1的时候就要处理
        if(pre.length == 1){
            return new TreeNode(rootVal);
        }
 
        //我们先找到root所在的位置，确定好前序和中序中左子树和右子树序列的范围
        TreeNode root = new TreeNode(rootVal);
        int rootIndex = 0;
        for(int i=0;i<in.length;i++){
            if(rootVal == in[i]){
                rootIndex = i;
                break;
            }
        }
 
        //递归，假设root的左右子树都已经构建完毕，那么只要将左右子树安到root左右即可
        //这里注意Arrays.copyOfRange(int[],start,end)是[)的区间
        root.left = reConstructBinaryTree(Arrays.copyOfRange(pre,1,rootIndex+1),Arrays.copyOfRange(in,0,rootIndex));
        root.right = reConstructBinaryTree(Arrays.copyOfRange(pre,rootIndex+1,pre.length),Arrays.copyOfRange(in,rootIndex+1,in.length));
 
 
        return root;
    }
}

 

// 上面逻辑参考

 

 

 

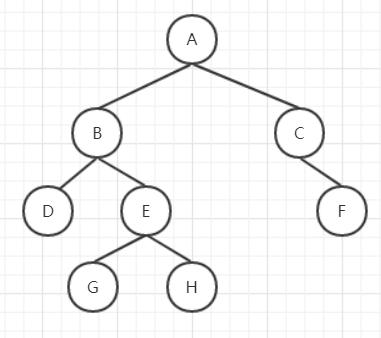
前序遍历：根结点 —> 左子树 —> 右子树（先遍历根节点，然后左右）
这棵树的前序遍历为：ABDEGHCF

中序遍历：左子树—> 根结点 —> 右子树（在中间遍历根节点）
这棵树的中序遍历为：DBGEHACF

后序遍历：左子树 —> 右子树 —> 根结点（最后遍历根节点）
这棵树的后序遍历为：DGHEBFCA

层次遍历：按层次遍历
这棵树的层次遍历为：ABCDEFGH
————————————————

所谓的前序、中序、后续，就是对根节点而言的，左右的遍历顺序不变，前序就是根节点最先遍历，然后左右；中序就是把根节点放在中间遍历；后序则是把根节点放在最后遍历