一道题目的分享---三角形判断的程序优化

一道题目的分享

 

 

 

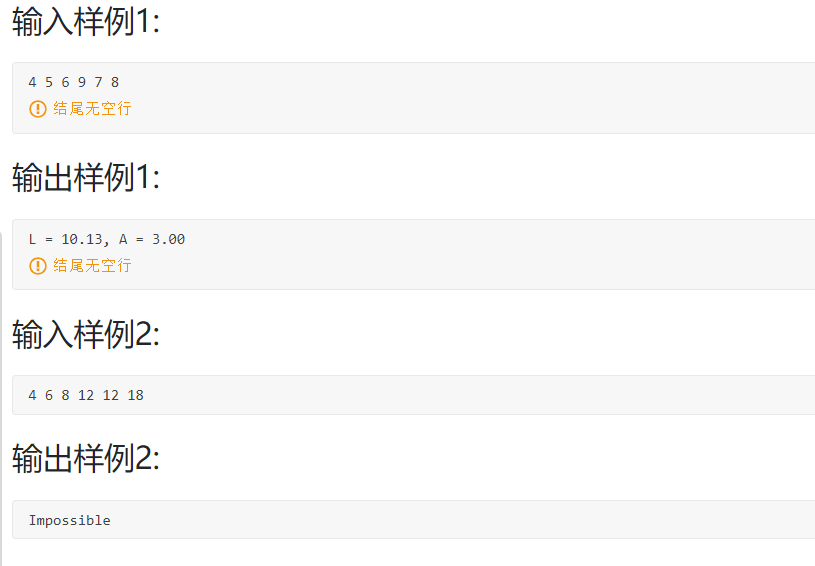
初步分析：

输入三个点坐标，涉及到平面直角坐标系中距离的计算，需要调用sqrt函数。其次需要利用三角形的性质判断三边是否可以构成一个三角形。最后周长计算直接将三边之长相加。但面积计算需要利用割补法，补全一个矩形再进行面积计算。综上，考虑到判断的条件比较复杂，面积计算麻烦，我们需要优化算法。

 

再分析：（1）考虑到海伦公式可以用来求面积，delta可以用来判断三边是否可以构成三角形。我们利用海伦公式优化程序。

 

 

（2）对于平面直角坐标系中距离的计算，有明确的公式，因此我们可以定义一个函数，还可以方便日后使用。

 

流程图

 

 

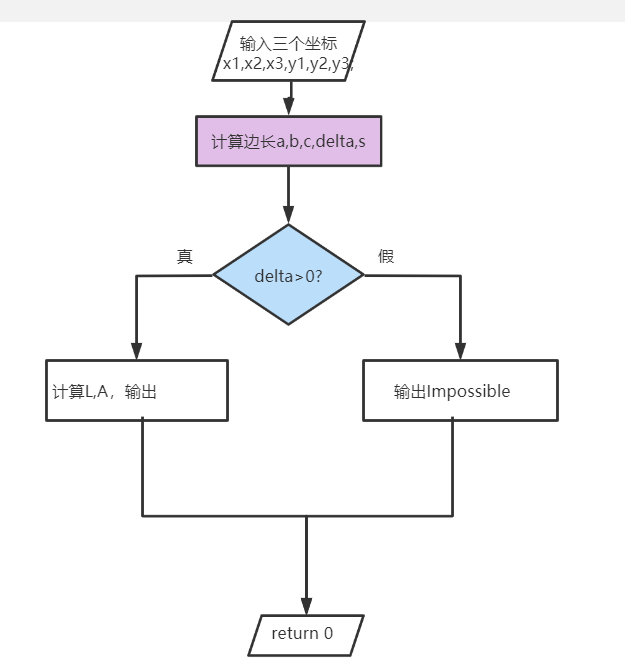
 代码段

#include <stdio.h>

double len(double a,double b,double c,double d){

       double re;

       re=sqrt((c-a)*(c-a)+(d-b)*(d-b));

       return re;

}

int main(){

 

    double x1,x2,x3,y1,y2,y3;

    double a,b,c,delta,L,A,s;

    scanf("%lf %lf %lf %lf %lf %lf",&x1,&y1,&x2,&y2,&x3,&y3);

      a=len(x1,y1,x2,y2);

      b=len(x2,y2,x3,y3);

      c=len(x1,y1,x3,y3);//距离的计算

      s=(a+b+c)/2;

  delta=(s-a)*(s-b)*(s-c);//判断

  if(delta<=0) printf("Impossible\n");

    else{

        L=2*s;

        A=sqrt(s*delta);

        printf("L = %.2lf, A = %.2lf\n",L,A);

       }