傅里叶变换（2）

傅里叶变换的粗犷理解

　　傅里叶变换是用来将信号波形从时域转成频域的分析方法，以往通过时域来分析信号波形的好处是准确了解每个时刻波形的幅度。我们知道任何周期信号都能认为是若干个三角函数信号的叠加。所以，从频域分析能很简单地看出周期信号的组成。这里 放一个经典的图。

 

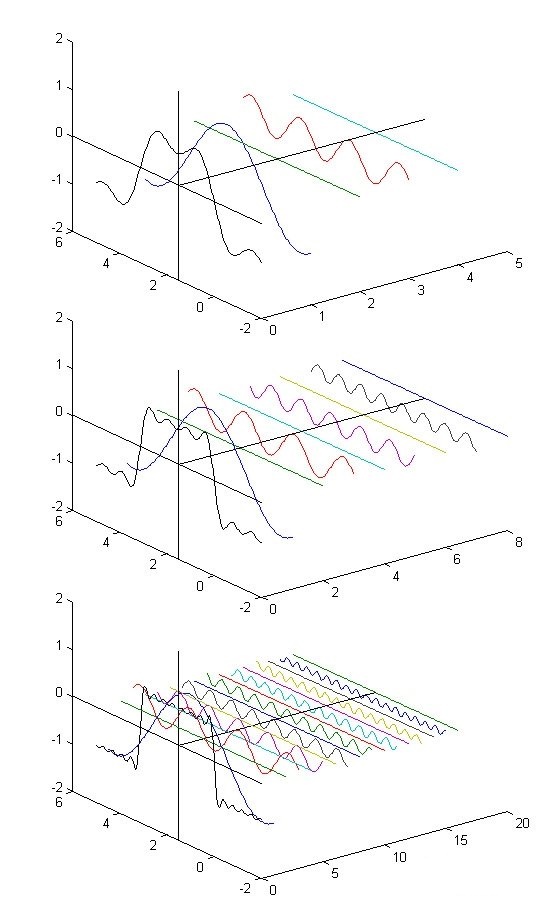
　　左侧的纵轴是幅度，中间的X轴是时间轴，右侧的Z轴是频率。所以方波就是由无穷个正弦波叠加而来的，这也是傅里叶级数的基本内容。我们从右侧Z轴看去，那么方波的频谱就是无穷个幅值依次减小的正弦波。

　　这里给出傅里叶变换的公式：

 

 

 

　　其反变换的公式我就不写了，用得少。

　　按照国外某个科普视频（https://www.bilibili.com/video/BV1qi4y1t7JY）的理解思路走，可以将上面的公式用欧拉公式化简一下。

 

　　注意f(t)是一个单纯的实数，但是F(ω)就有可能是一个复数了，它有一个虚数单位j在里面。当f(t)=cos(πt)时，这里举一个偶函数方便叙述，上面公式的后半部分可以去掉因为其积分为0。

　　再次将其变换下，上面的公式变为：

 

　　这里我就懒得去算了，好像并不好算。结果是除了ω=±π，F(ω)为正无穷之外，ω取任意值，F(ω)都是0。不光是f(t)=cos(πt)时，有这种情况，f(t)为周期函数时都有这种情况。那么其傅里叶变换后的图象为：

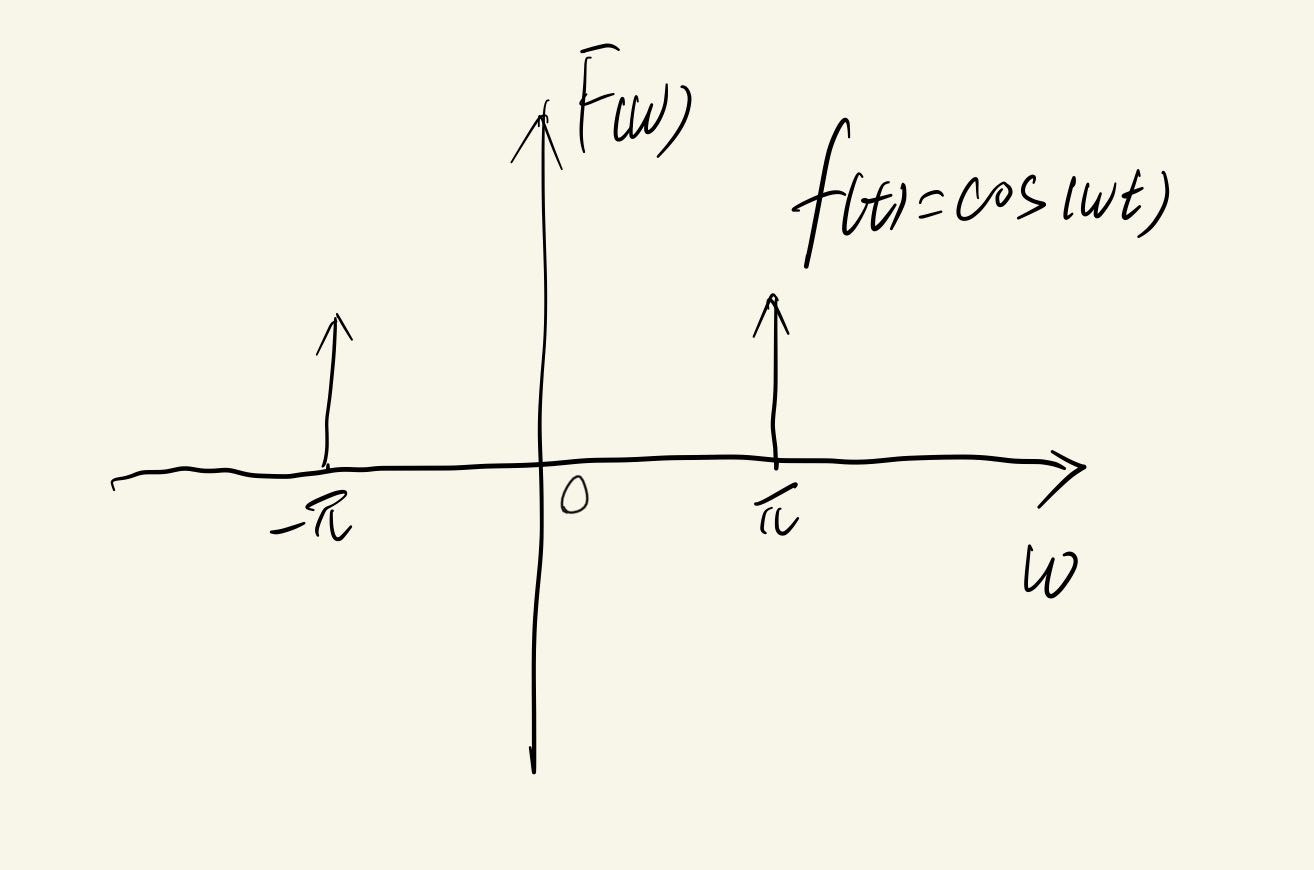
　　大概就是这样。