基于移动最小二乘法的点云曲面拟合（python）

1.移动最小二乘法介绍

  为了更好地对数据量大且形状复杂的离散数据进行拟合，曾清红等人^[1]开发出一种新的算法——移动最小二乘法。这种新的最小二乘算法为点云数据的处理提供了新的方法。使用点云数据拟合曲面时，由于点云的数据量大、形状复杂的特点，如果使用传统的最小二乘法拟合可能会得到病态的曲面方程，从而导致较大的误差。而使用移动最小二乘法拟合点云不仅能够减少误差，提升局部的准确率，还能避免分块拟合和平滑化的过程。下图为子区域的划分示意图。

                             

                         

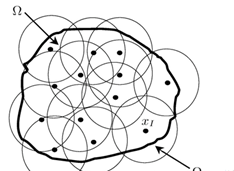
  通过某点确定一个子区域，在该区域内，移动最小二乘法是根据区域内的空间点加权拟合方程，并根据拟合方程解算这一点的坐标。使用移动最小二乘法拟合点云曲面可以看作是一个插值的过程，每一次插值都对应着一次加权最小二乘的方程拟合，所以它可以逼近曲面但不能得到曲面方程。

  关于该算法的原理叙述请参看曾清红, 卢德唐. 基于移动最小二乘法的曲线曲面拟合。

2.程序设计

　　在某个子区域中可能会出现空间点数量过少或分布复杂不规律的情况，这会导致最小二乘法解算方程系数时出现奇异矩阵。一般做法是迭代调整阈值，直到子区域内的空间点数量分布符合拟合要求，但这种方法复杂度较高且在点云本身分布失常的情况下调整阈值没有意义。为了方便，我们在点云分布不均匀导致出现奇异矩阵的情况下，引入几何中心（也可以根据情况选择其他方法）代替最小二乘的方程求解。

# -*- coding: utf-8 -*-
"""
Created on Sat Apr 11 17:39:16 2020

@author: L JL
"""
import numpy as np 
import matplotlib.pyplot as plt 
from mpl_toolkits.mplot3d import Axes3D

f = open('xuanze.txt','r')
point = f.read()
f.close()
data1 = point.replace('\n',' ')
data2 = data1.split(' ')
data2.pop()
n = len(data2)
data2 = list(map(float,data2))

mat1 = np.array(data2[0:n]) 
mat2 = mat1.reshape(int(n/3),3)

mat3 = []

for each in mat2:
    each_line = list(map(lambda x:float(x),each))
    mat3.append(each_line)
mat4=np.array(mat3)
x = [k[0] for k in mat4]
y = [k[1] for k in mat4]
z = [k[2] for k in mat4]

def D_radius(x,y,X,Y,N):
    ind_mat = np.zeros((N,2))
    for i in range(N):
        s = ((x-X[i])**2+(y-Y[i])**2)**0.5
        ind_mat[i][0] = s
        ind_mat[i][1] = i
    ind_mat = ind_mat[np.lexsort(ind_mat[:,::-1].T)]
    return ind_mat
    
def W_mat(d,x0,y0,x,y): 
    s=(((x-x0)**2+(y-y0)**2)**0.5)/d
    #print((x-x0)**2+(y-y0)**2)
    #print(s)
    if (s<=0.5):
        return (2/3)-4*s**2+4*s**3 
    elif(s<=1):
        return (4/3)-4*s+4*s**2-(4/3)*s**3 
    else: return 0

def A_mat(W,P,M,N):
    A = []
    for m in range(M):
        a = []
        for n in range(M):
            #pmn = p_mn(W,P,N,m,n)
            pmn = 0
            for i in range(N):
                pmn = pmn + W[i]*P[i,m]*P[i,n]
            a.append(float(pmn))
        A.append(a)
    return A

def B_mat(u,W,P,M,N):
    B = []
    for i in range(M):
        sumB = 0
        for j in range(N):
            sumB = sumB + W[j]*P[j,i]*u[j]
        B.append(float(sumB))
    return B

X = np.array(x)
Y = np.array(y)
Z = np.array(z)
Xmax = int(np.max(X))
Xmin = int(np.min(X))
Ymax = int(np.max(Y))
Ymin = int(np.min(Y))


N = len(X)
M = 3
P = np.mat(np.zeros((N,M)))
W = np.mat(np.zeros((N,1)))
A = np.mat(np.zeros((M,M)))
B = np.mat(np.zeros((M,N)))
u = np.mat(Z).T
a = np.mat(np.zeros((M,1)))
d_mat = np.mat(np.zeros((N,1)))
#dataZ = []

dataX = np.arange(Xmin,Xmax,0.5)
dataY = np.arange(Ymin,Ymax,0.5)

print(Xmin,Xmax)
print(Ymin,Ymax)

f2 = open("dataZ.txt","w")
for i in dataX:
    for j in dataY:
        #d = D_radius(i,j,X,Y,N)
        d = 2
        ind_mat = D_radius(i,j,X,Y,N)
        #print(ind_mat)
        if ind_mat[3,0] <= d:
            try:
                W = np.mat(np.zeros((N,1)))
                for n in range(0,N):
                    P[n,0] = 1 
                    P[n,1] = X[n]
                    P[n,2] = Y[n] 
                    W[n] = W_mat(d,X[n],Y[n],i,j)
                #print(W)
                A = A_mat(W,P,M,N)
                B = B_mat(u,W,P,M,N)
                c = np.linalg.solve(A,B) 
                #dataZ.append(c[0]+c[1]*i+c[2]*j)
                dataZ = c[0]+c[1]*i+c[2]*j
                print('A')
                #print(dataZ)
            except:
                ind_Zsum = 0
                for ind in range(0,4):
                    ind_Zsum += Z[int(ind_mat[ind,1])]
                #dataZ.append(ind_Zsum/4)
                dataZ = ind_Zsum/4
                print('B')
                #print(dataZ)
        else:
            ind_Zsum = 0
            for ind in range(0,4):
                ind_Zsum += Z[int(ind_mat[ind,1])]
            #dataZ.append(ind_Zsum/4)
            dataZ = ind_Zsum/4
            print('C')
            #print(dataZ)
        f2.write(str(i) + ',' + str(j) + ',' + str(dataZ) + '\n')          
        print(i,j)

f2.close()        

# 3D绘图示意
import numpy as np 
import matplotlib.pyplot as plt 
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = Axes3D(fig)
Xmin = -82
Xmax = 23
Ymin = 0
Ymax = 42

x = np.arange(Xmin, Xmax, 0.5)
y = np.arange(Ymin, Ymax, 0.5)

y,x  = np.meshgrid(y, x)

f = open('dataZ.txt','r')
point = f.read()
f.close()
data1 = point.replace('\n',',')
data2 = data1.split(',')
data2.pop()
n = len(data2)
data2 = list(map(float,data2))

mat1 = np.array(data2[0:n])
mat2 = mat1.reshape(int(n/3),3)

z = mat2[:,2].reshape(x.shape)
'''
print("网格化后的X=",x)
print("X维度信息",x.shape)
print("网格化后的Y=",y)
print("Y维度信息", y.shape)
print("网格化后的Z=",z)
'''

ax.plot_surface(x, y, z, cmap=plt.cm.hot)      # 渐变颜色
#ax.contourf(x, y, z,cmap=plt.cm.hot)
ax.set_xlabel('X Label (m)')
ax.set_ylabel('Y Label (m)')
ax.set_zlabel('Z Label (m)')
ax.set_title('Point Cloud Surface Fitting')
plt.show()

 

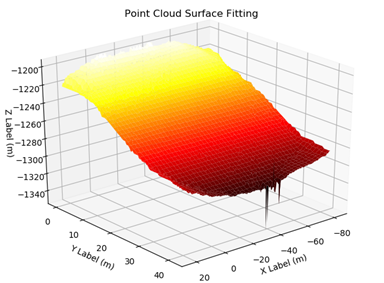
3.拟合情况及存在的问题

  其他点云的拟合情况，如下图所示。

 

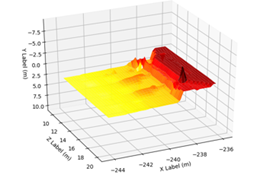
  （1）部分区域出现拟合异常；

  （2）程序计算量大，复杂度太高，有待优化；

  （3）对高分辨率点云，通过调整步长，可以调整插值步数，提高精度。

 

参考文献：

  [1] 曾清红, 卢德唐. 基于移动最小二乘法的曲线曲面拟合 [J]. 工程图学学报, 2004