day58 动态规划part15 代码随想录 392. 判断子序列

题目：392. 判断子序列

我的感悟：

• 不会就抄一遍，把DP打印出来，多理解理解。
• 完成比完美更重要！

理解难点：

• 我现在外层，内层有点不会了

听课笔记：

我的代码：

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        # 外s i 
        # 内t j
        dp = [[0]*(len(t)+1) for _ in range(len(s)+1)]
        for i in range(1,len(s)+1):
            for j in range(1,len(t)+1):
                if s[i-1] == t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = dp[i][j-1]
        if dp[-1][-1] == len(s):
            return True
        return False 

通过截图：

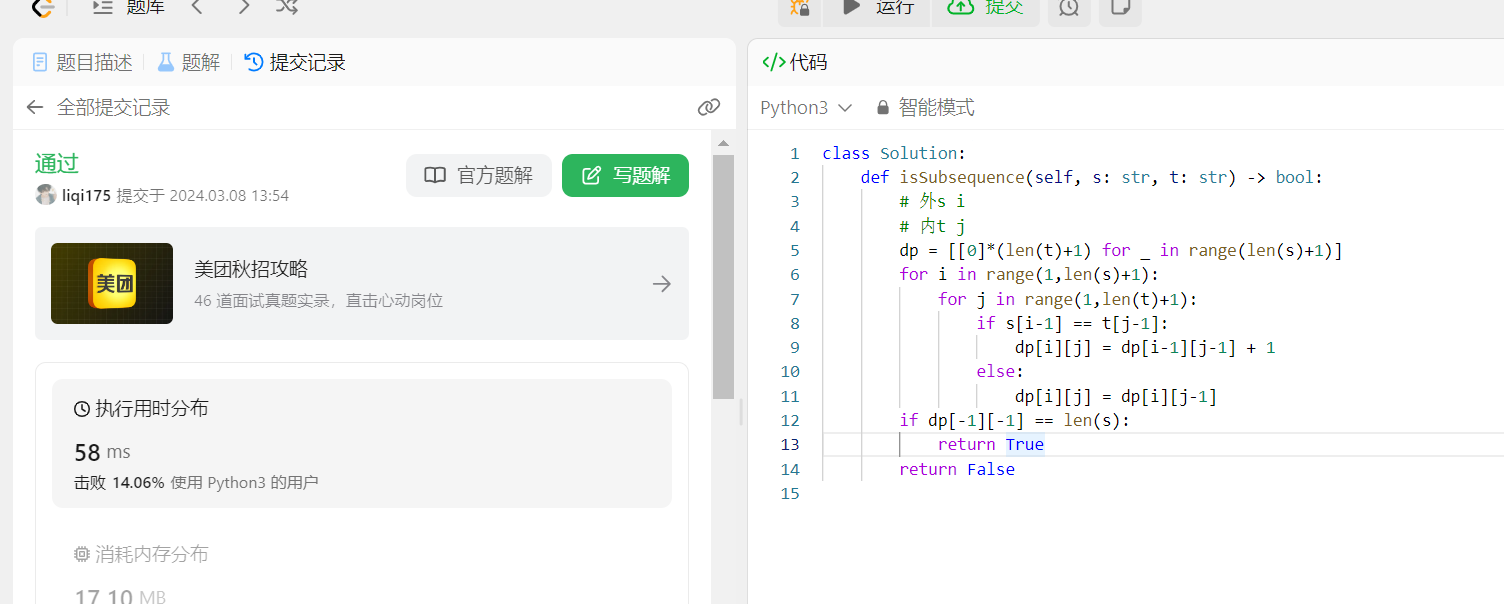
双指针自己写了一遍：

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        # 双指针 t长
        a,b = 0,0
        while b< len(t):
            if a < len(s) and s[a] == t[b]: # 防止越界
                a+=1
            b+=1
        if a == len(s):
            return True
        
        return False

双指针易错点：

• s="" ,t = "ahbgdc" 这种用例,s是为空的,要添加 a < len(s) 边界判断

扩展写法-双指针：

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        # 初始化两个指针，分别指向s和t的第一个字符
        i, j = 0, 0
        
        # 遍历t，直到j到达t的末尾
        while j < len(t):
            # 如果当前t的字符与s的第i个字符相同
            if i < len(s) and t[j] == s[i]:
                # 匹配成功，移动s的指针到下一个字符
                i += 1
            
            # 移动t的指针到下一个字符
            j += 1
        
        # 如果s的指针i到达了s的末尾，说明s是t的子序列
        return i == len(s)

AI分析：

在这个代码中，我们使用两个指针i和j分别遍历字符串s和t。我们从t的第一个字符开始遍历，每当找到一个与s当前字符匹配的字符时，就将s的指针向前移动一位。如果s的指针能够遍历完整个s，那么s就是t的子序列。

这种方法的效率比之前的方法要高，因为它避免了在每次迭代中都遍历整个t。在最坏的情况下，我们只需要遍历s和t中的每个字符一次。因此，时间复杂度是线性的，即O(m + n)。

扩展写法-迭代器：

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
    	# 判断 s 是否为 t 的子序列。
    	b = iter(t)  # 迭代器
    	return all(((i in b) for i in s ))

AI辅助分析：

时间复杂度是O(m * n)，其中m是子序列字符串s的长度，n是目标字符串t的长度。

1. 创建迭代器b = iter(t)的时间复杂度是O(1)，因为它仅仅是创建一个迭代器，不涉及遍历t。

2. all(((i in b) for i in s))这部分是一个列表推导式，它遍历字符串s中的每个字符，并检查该字符是否在迭代器b代表的字符串t中。对于s中的每个字符i，(i in b)这个操作的时间复杂度是O(n)，其中n是t的长度。这是因为在最坏的情况下，可能需要遍历整个t来确定字符i是否存在。

3. 由于列表推导式会为s中的每个字符执行上述操作，所以总的时间复杂度是O(m * n)，其中m是s的长度，n是t的长度。

资料：

代码随想录