矩阵计算(导数)
1 标量的导数
2 亚导数
比如说\(y=|x|\)这个函数在x=0的时候时不可导的。当x>0，其到导数为1，x<0，其导数为-1，所以在x=0的这个地方的亚导数就是可以是[-1,1]中的一个数
矩阵求导
向量化的优点
1.简洁
比如说：
\(
\begin{split}\begin{cases}
y_1=W_1*X_{11}+W_2*X_{12}+...+W_n*X{1n}\\
y_2=W_1*X_{21}+W_2*X_{22}+...+W_n*X{1n}\\
.....\\
y_n=W_1*X_{n1}+W_2*X_{n2}+...+W_n*X{nn}\\
\end{cases}\end{split}\)
这个函数可以简化成
2.加速计算机的计算
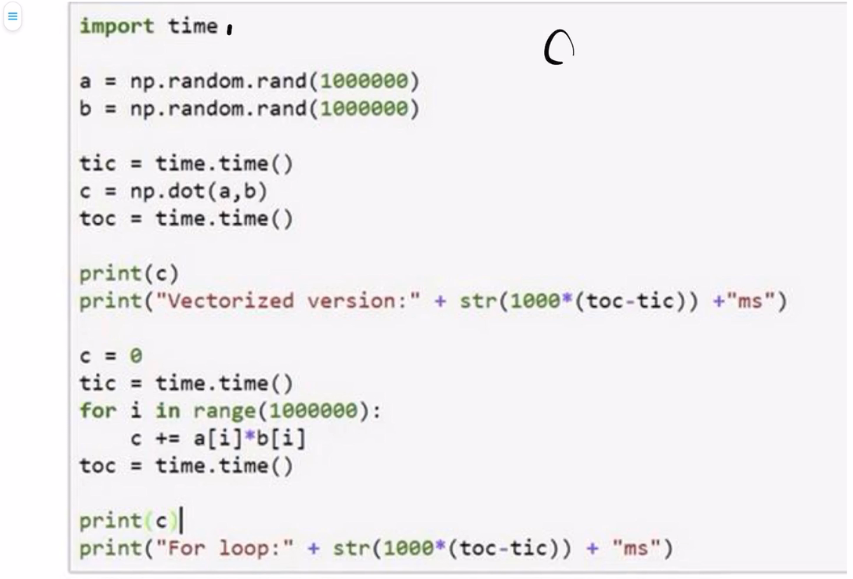
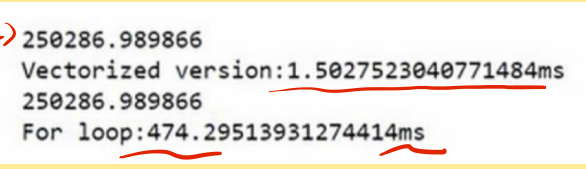
对于同样一个矩阵相乘的操作，我们可以我们可以看出用矩阵的话是1.5ms，但是如果用for循环的话是474ms。
标量函数和向量函数
标量函数
其实标量函数就是最后运算之后输出为标量的函数，例如：
- \(f(x)=x^2,其中x->x^2\)
- \(f(x)=x_1^2+x_2^2\),其中\(\begin{bmatrix} X_1\\ X_2\\ \end{bmatrix}=>X_1^2+X_2^2\)
这两个最终的运算结果都是一个标量。
向量函数
就是最后运算结果为一个向量，例如：
① \(f(x)=\begin{bmatrix}
f_1(x)=X\\
f_2(x)=X^2\\
\end{bmatrix}, x->\begin{bmatrix}
X\\
X^2\\
\end{bmatrix}\)
② \(f(x)=\begin{bmatrix} f_1(x)=X,f_2(x)=X^2\\ f_3(x)=X^3,f_4(x)=X^4\\ \end{bmatrix}, 其中：x->\begin{bmatrix} X,X^2\\ X^3,X^4\\ \end{bmatrix}\)
③ \(f(x)=\begin{bmatrix} f_1(x)=X_1+X_2,f_2(x)=X_1^2+X_2^2\\ f_3(x)=X_1^3+X_2^3,f_4(x)=X_1^4+X_2^4\\ \end{bmatrix} , \begin{bmatrix} X_1\\ X_2\\ \end{bmatrix} ->\begin{bmatrix} X_1+X_2,X_1^2+X_2^2\\ X_1^3+X_2^3,X_1^4+X_2^4\\ \end{bmatrix}\)
矩阵求导
\(\frac{dA}{dB}\):矩阵求导的本质就是矩阵A中的每一个元素对矩阵B中的每个元素求导。
然后从求导后的元素个数角度：
因为他是矩阵A中的每个元素对矩阵B中的每个元素，所以是这样的形状。
| A | B | \(\frac{dA}{dB}\) |
|---|---|---|
| $$1\times1$$ | $$1\times 1$$ | $$1\times 1$$ |
| $$1\times p$$ | $$1\times n$$ | $$p\times n$$ |
| $$q\times p$$ | $$m\times n$$ | $$p\times q\times m\times n$$ |
求导方法
\(YX\)拉伸，其中\(Y\)横向拉伸，\(X\)纵向拉伸。
这里的前面，后面指的是\(YX\)或者是\(XY\)，这里本文用的是\(YX\)。
例一：f(x)标量，x向量
\(\frac{df(x)}{dx}\),其中f(x)就是Y,f(x)为标量函数，x为向量。也就是\(f(x)=f(x_1,x_2,x_3...x_n),x=[x_1,x_2,x_2...n]^T\)
我们按照上面的规则，f(x)是标量不变，拉伸，X纵向拉伸。
这个实际上就是将多元函数的偏导写在一个列向量中。
例二：f(x)向量，x标量
\(\frac{df(x)}{dx}\),f(x)为向量函数，x为向量。也就是\(f(x)=\begin{bmatrix}
f_1(x)\\
f_2(x)\\
...\\
f_n(x)\\
\end{bmatrix}\),然后这个f(x)横向拉伸,x不变。
最终结果就是:
\(\frac{df(x)}{dx}=\begin{bmatrix}
\frac{\partial f_1(x)}{\partial x},\frac{\partial f_2(x)}{\partial x}...\frac{\partial f_n(x)}{\partial x}\\
\end{bmatrix}\)
例三：f(x)为向量函数,x为向量函数
\(f(x)=\begin{bmatrix}
f_1(x)\\
f_2(x)\\
...\\
f_n(x)\\
\end{bmatrix}，x=\begin{bmatrix}
x_1\\
x_2\\
...\\
x_n\\
\end{bmatrix}\)
然后我们按照我们的规则，前面的横向拉伸，后面的纵向拉伸，然后本质就是A中的每个元素对矩阵B中的每一个求导。
我们看完上面这个对矩阵求导后的形状应该就了解了，上面的图也应该就知道了。
常见矩阵求导公式的推导
例一：\(f(x)=A^T*X\),求\(\frac{df(x)}{dx}\)
其中:
\(A=\begin{bmatrix}
a_1\\
a_2\\
...\\
a_n\\
\end{bmatrix}，x=\begin{bmatrix}
x_1\\
x_2\\
...\\
x_n\\
\end{bmatrix}\)
我们可以看出f(x)是标量，x是向量。
解：\(f(x)=A^T*X=\sum^n_1{a_i*x_i}\)
所以要把x纵向展开
\(\frac{df(x)}{dx}=\begin{bmatrix}
\frac{\partial f(x)}{\partial x_1}\\
\frac{\partial f(x)}{\partial x_2}\\
\frac{\partial f(x)}{\partial x_3}\\
...\\
\frac{\partial f(x)}{\partial x_n}\\
\end{bmatrix}=\begin{bmatrix}
a_1\\
a_2\\
a_3\\
...\\
a_n\\
\end{bmatrix}=A\)
ps：这里\(\frac{\partial f(x)}{\partial x_1}=a_1\)是因为\(f(x)=\sum^n_1{a_i*x_i}\),对于除了\(a_1*x_1\)在外的其他项，对\(x_1\)求偏导都是0。
也可以这样看，\(\frac{d(A^T*X)}{dx}=\frac{d(X^T*A)}{dx}=A\)
例二：\(f(x)=X^T*A*X\)
这个可以自己证明一下，最终结果为\(（A+A^T）X\).
两种布局
- 两种布局:
- 向量求导时的拉伸方向:
都是前面的横向拉伸，后面的纵向拉伸
-
YX拉伸术-->分母布局
Y横向拉伸(f(x)横向拉伸)
X纵向拉伸 -
XY拉伸术-->分子布局
X横向拉伸
Y纵向拉伸(f(x)横向拉伸)
梯度
这里主要搞得清楚他的形状
下面我们都使用的是分子布局（XY拉伸术），也就是X横向拉伸，Y纵向拉伸
-
∂y/∂x
当y是标量，x是向量的时候：
这里注意一点，你的梯度指向的是你的值变大的方向。
我们将X横向拉伸 -
∂y/∂x
当y是向量，x是标量的时候：
-
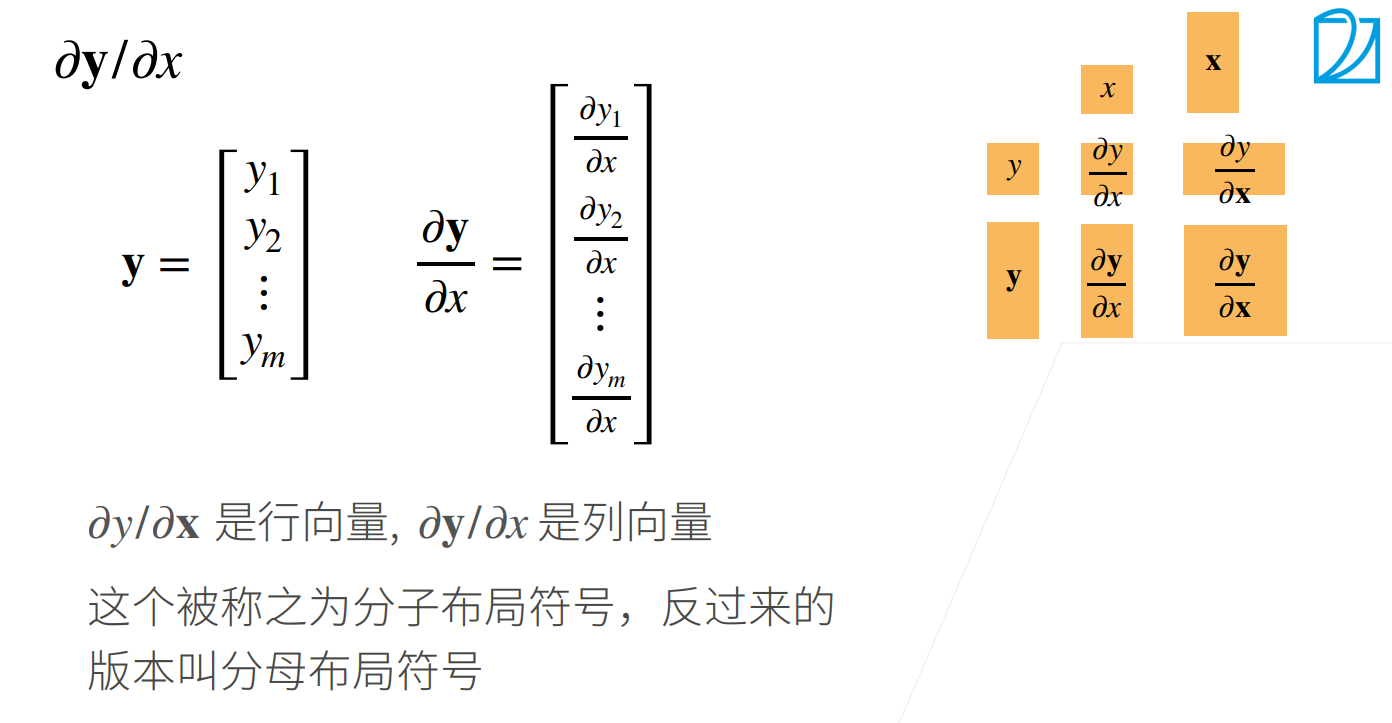
∂y/∂x
我们可以发现\(（分子布局）^T=（分母布局）\)
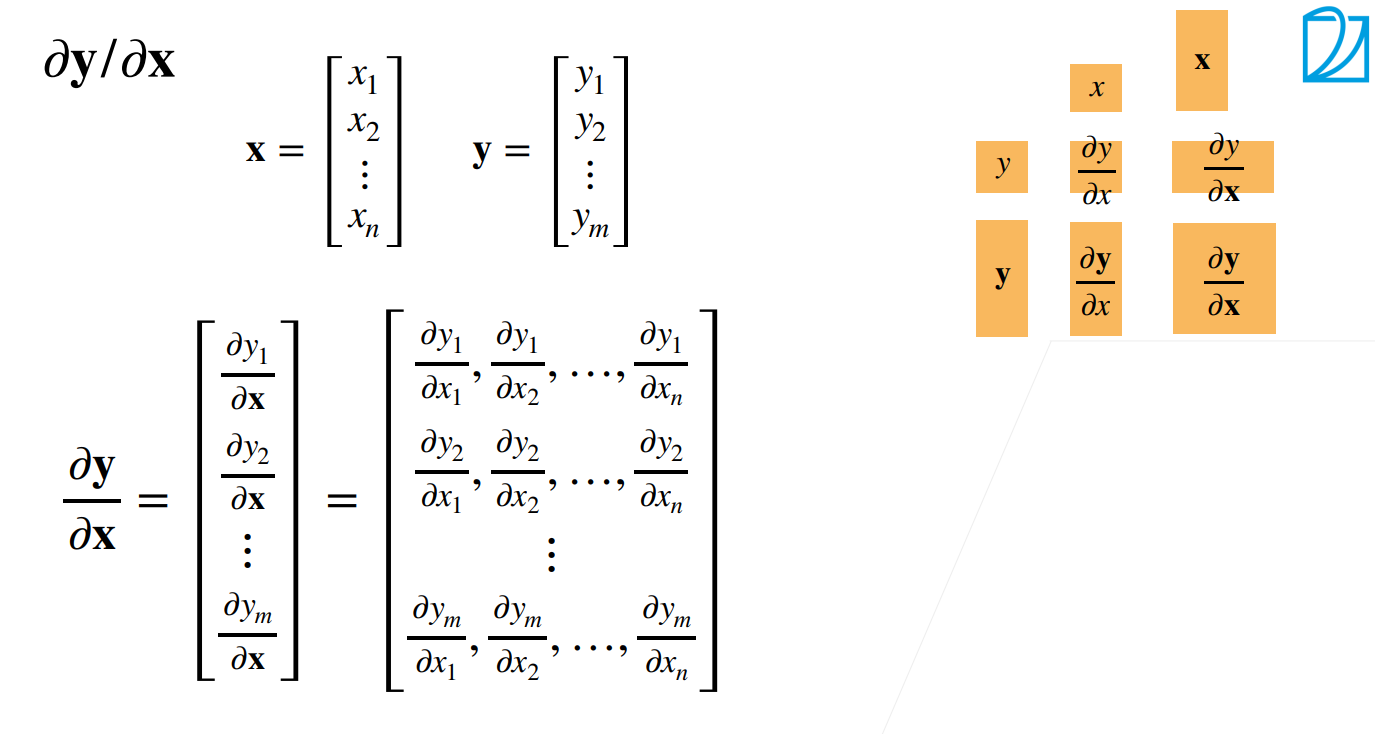
然后我们拓展的矩阵：
pytorch 自动求导
向量的链式法则
- 标量的链式法则
\(y=f(x),u=g(x),\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}*\frac{\partial u}{\partial x}\)
- 拓展到向量
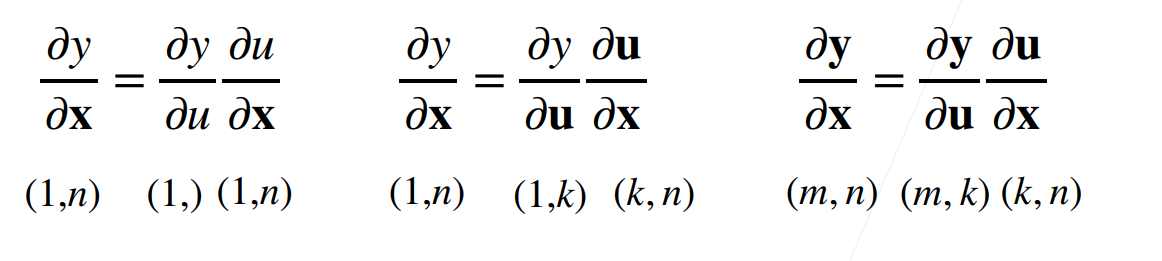
例一：
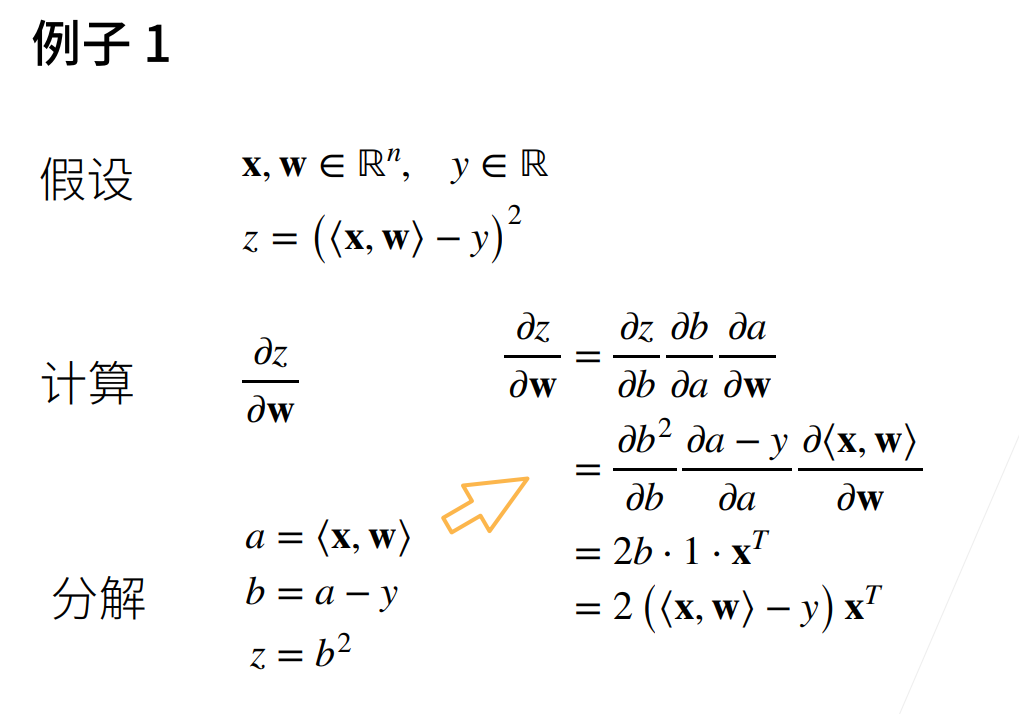
例二：
自动求导
自动求导计算一个函数在指定值上的导数
它有别于
- 符号求导（显式求导）
- 数值求导（隐式求导）
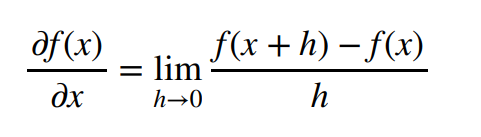
计算图
·将代码分解成操作子
·将计算表示成一个无环图
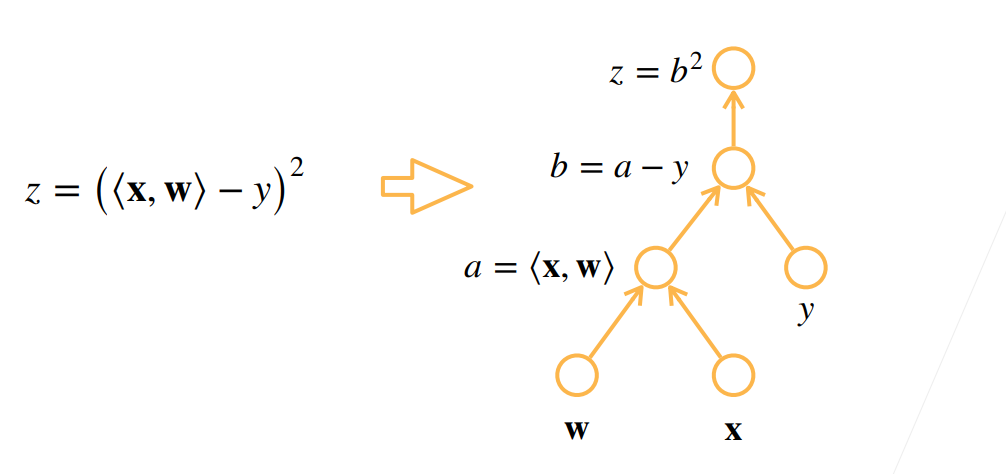
·将代码分解成操作子
·将计算表示成一个无环图
·显示构造
·将代码分解成操作子
·将计算表示成一个无环图
·显式构造
.Tensorflow/Theano/MXNet
·隐式构造
.PyTorch/MXNet
自动求导的两种模式
正向积累和反向传播（反向积累）
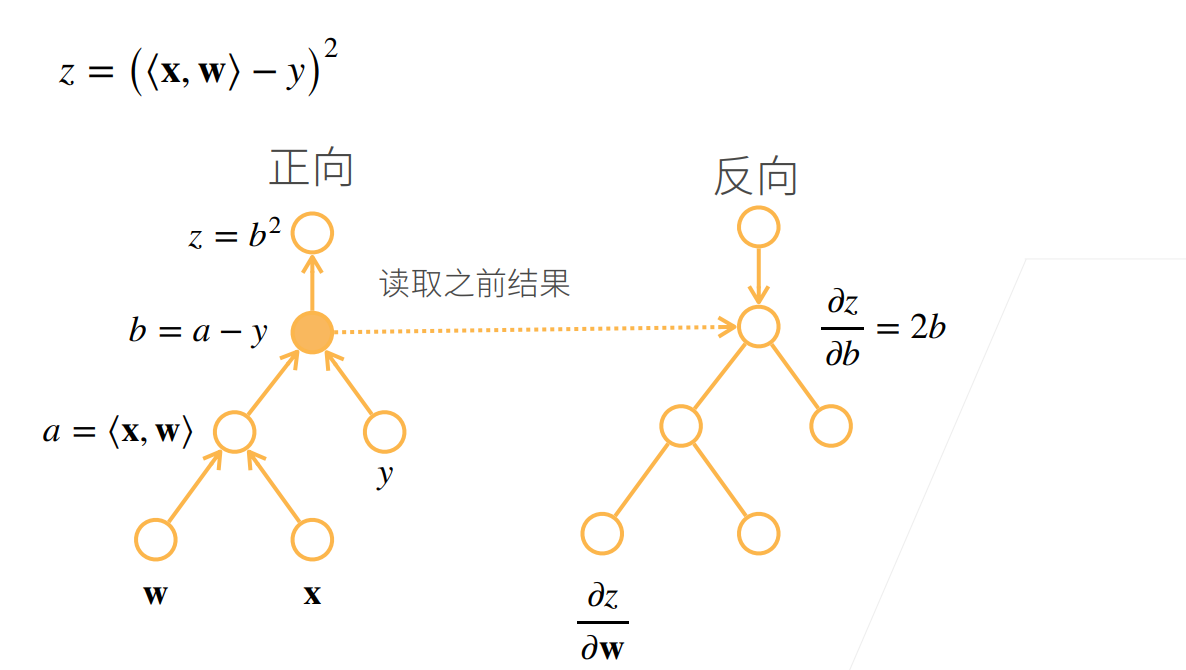
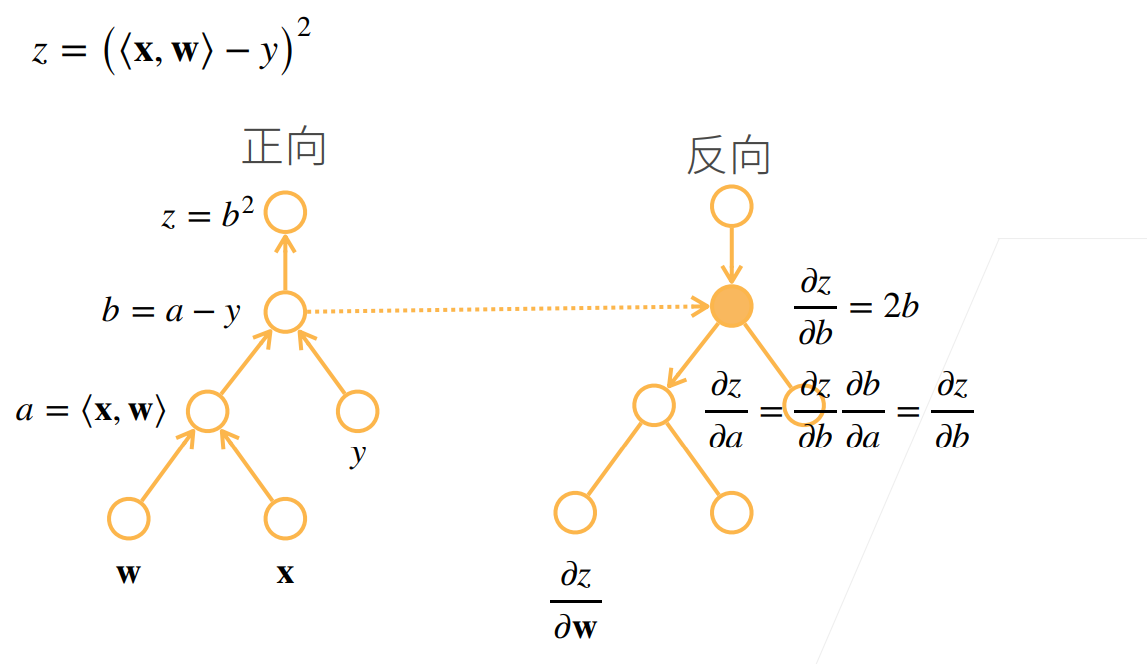
对于反向积累
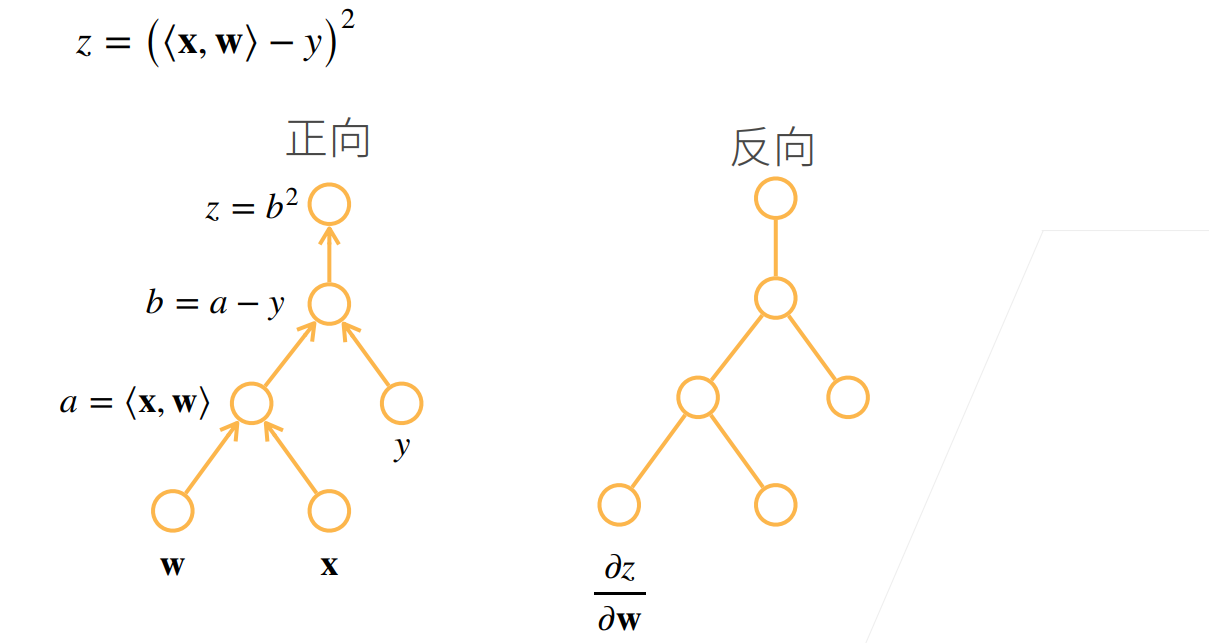
他需要读取之前的结果
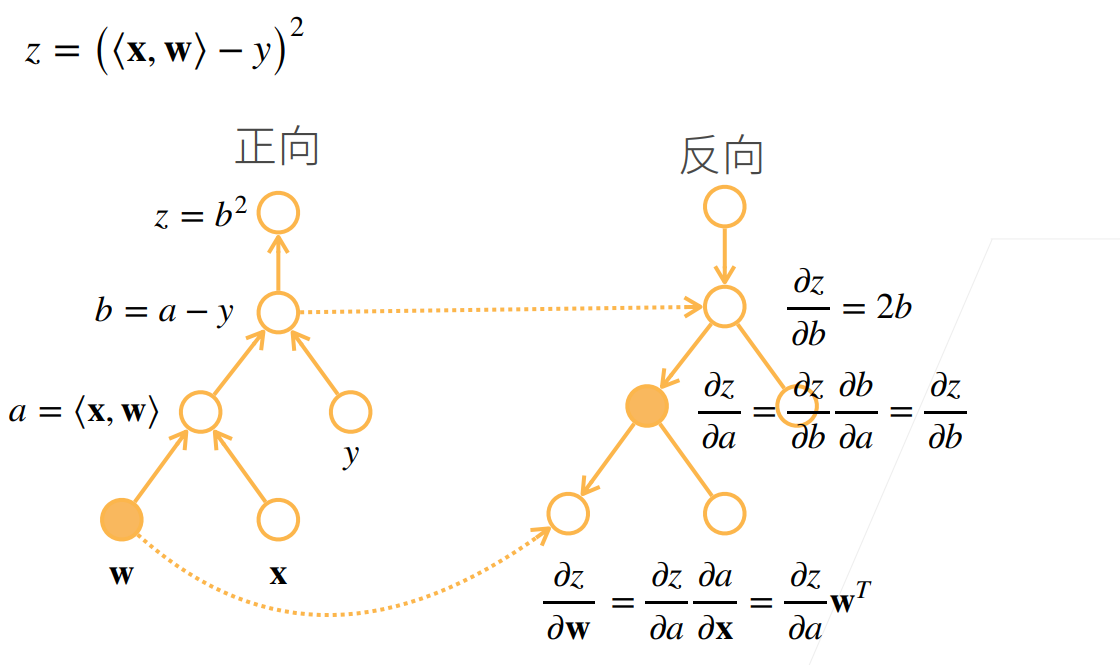
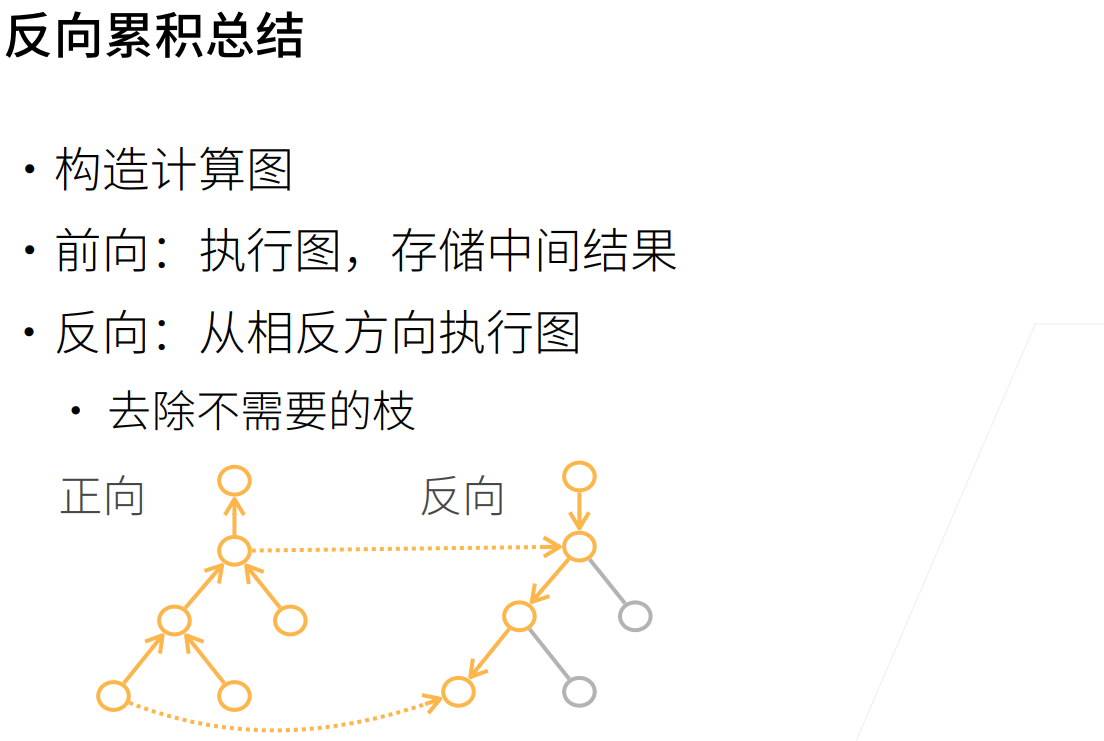
自动求导的实现
假设我们想对函数\(y=2x^⊤x\)关于列向量x求导，最终计算的结果是个标量
import torch
x = torch.arange(4.0)
x
# tensor([0., 1., 2., 3.])
在我们计算y关于x的梯度之前，我们需要一个地方来存储梯度
x.requires_grad_(True)
x.grad
requires_grad: 如果需要为张量计算梯度，则为True，否则为False。我们使用pytorch创建tensor时，可以指定requires_grad为True（默认为False)，创建一个Tensor并设置requires_grad=True，requires_grad=True说明该变量需要计算梯度。
grad：当执行完了backward()之后，通过x.grad查看x的梯度值。
在这里我们可以在创建完x之后再x.requires_grad_(True)，或者我们创建的时候就
`x = torch.arange(4.0,requires_grad=True)``
现在让我们计算y
y = 2 * torch.dot(x, x)
y
# tensor(28., grad_fn=<MulBackward0>)
通过调用反向传播函数来自动计算y关于x每个分量的梯度
y.backward()
x.grad
# tensor([ 0., 4., 8., 12.])
x.grad == 4 * x
# tensor([True, True, True, True])
\(y=2x^⊤x\)然后他的函数求导之后的值和4*x一样的。
现在让我们计算x的另一个函数
x.grad.zero_()是让他的梯度清空
x.grad.zero_()
y = x.sum()
y.backward()
x.grad
# tensor([1., 1., 1., 1.])
深度学习中 ，我们的目的不是计算微分矩阵，而是批量中每个样本单独计算的偏导数之和
x.grad.zero_()
y = x * x
y.sum().backward()
x.grad
# tensor([0., 2., 4., 6.])
将某些计算移动到记录的计算图之外
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u
# tensor([True, True, True, True])
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x
# tensor([True, True, True, True])
即使构建函数的计算图需要通过Python控制流（例如，条件、循环或任意函数调用），我们仍然可以计算得到的变量的梯度
def f(a):
b = a * 2
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
a.grad == d / a
# tensor(True)
