TensorFlow10.1 卷积神经网络-卷积与卷积神经网络
1 卷积神经网络的引入
这个主要是应对2D的图片处理产生的。
灰色的图片的表示：[b,h,w,1]
彩色的图片的表示：[b,h,w,3]
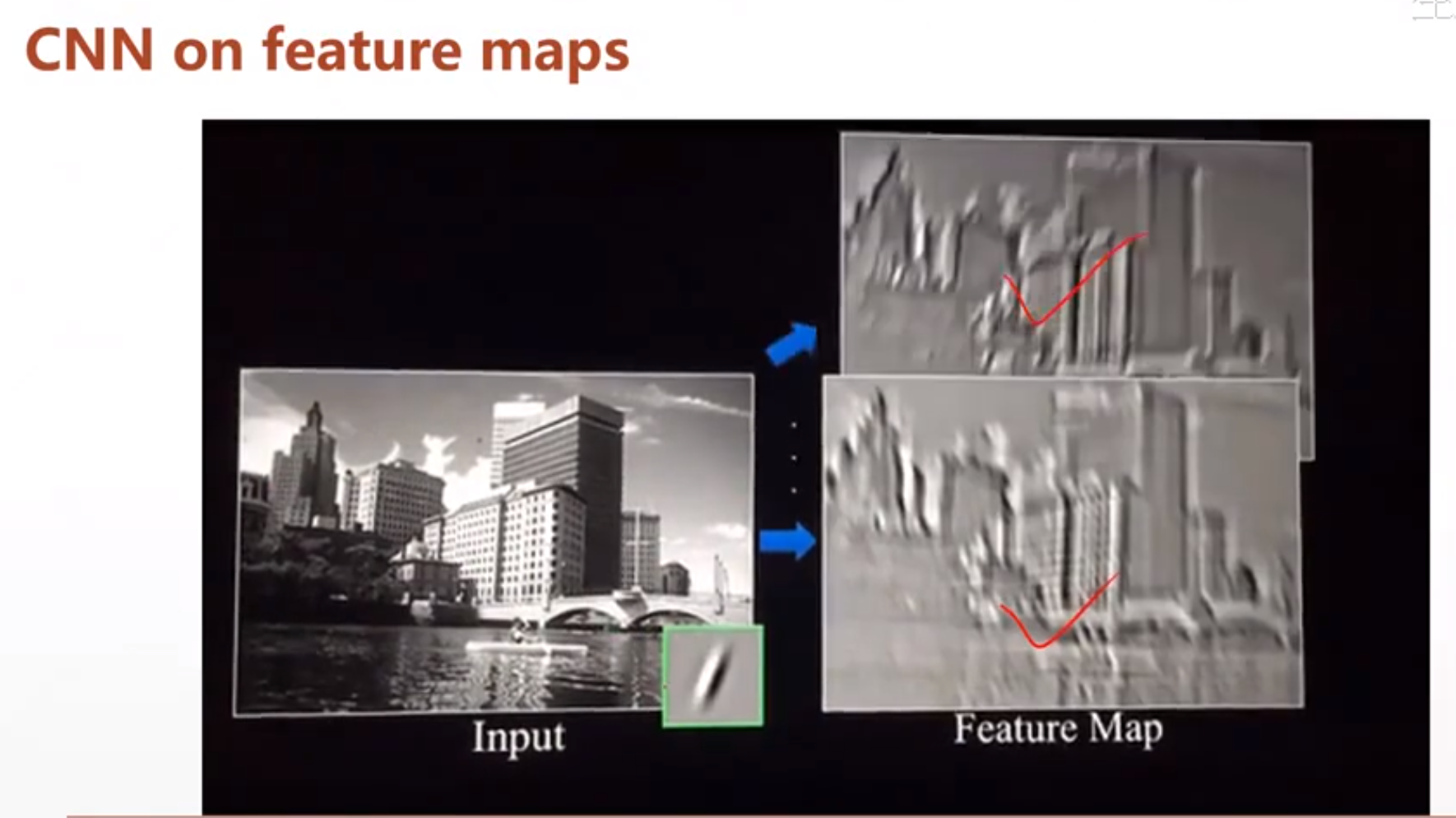
然后这个Feature maps:
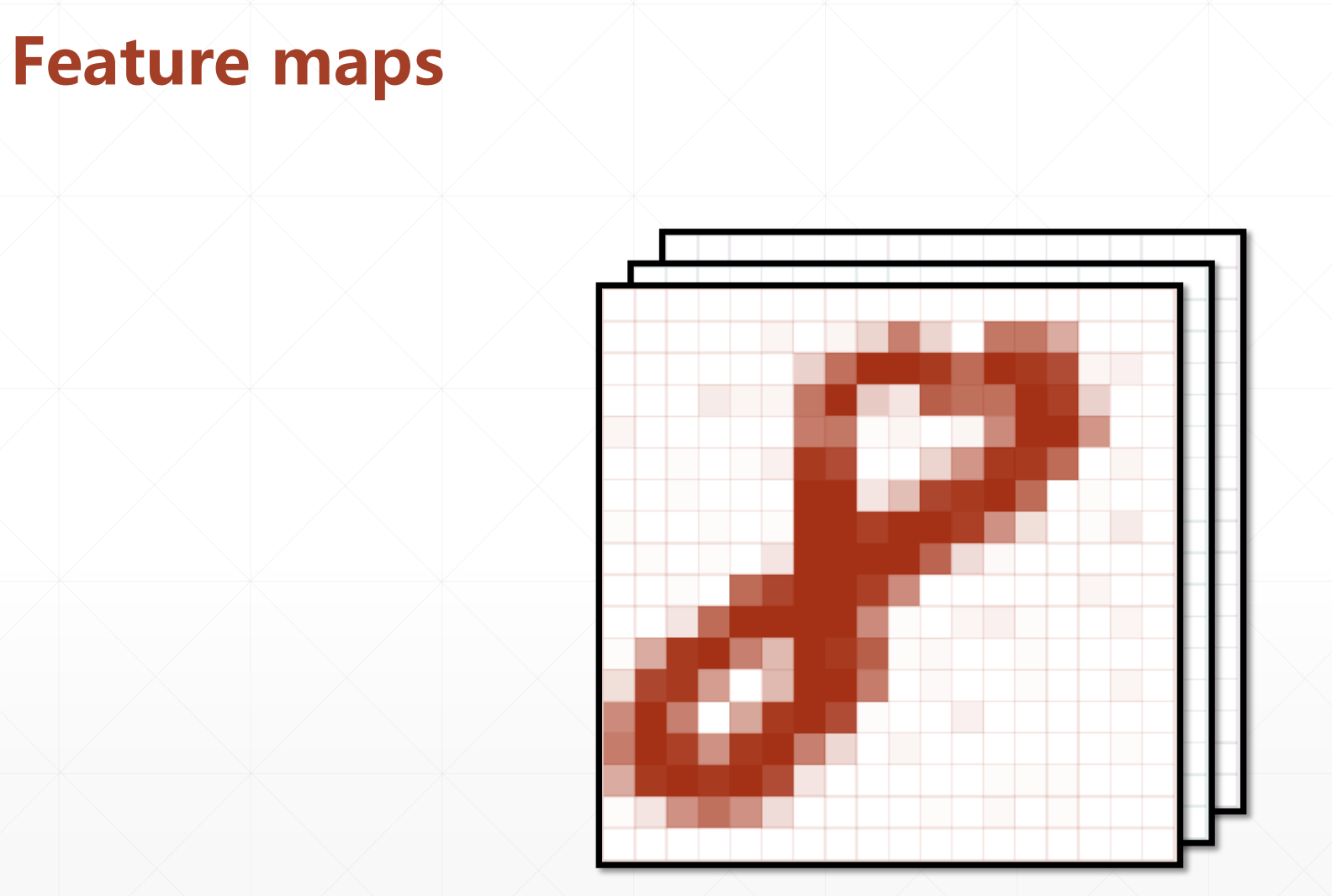
越往上他的维度会变得越小，最后可能经过一个全连接层，变成[b,10]。
对于一个图片的处理，在这里我们为什么不用全连接神经网络：
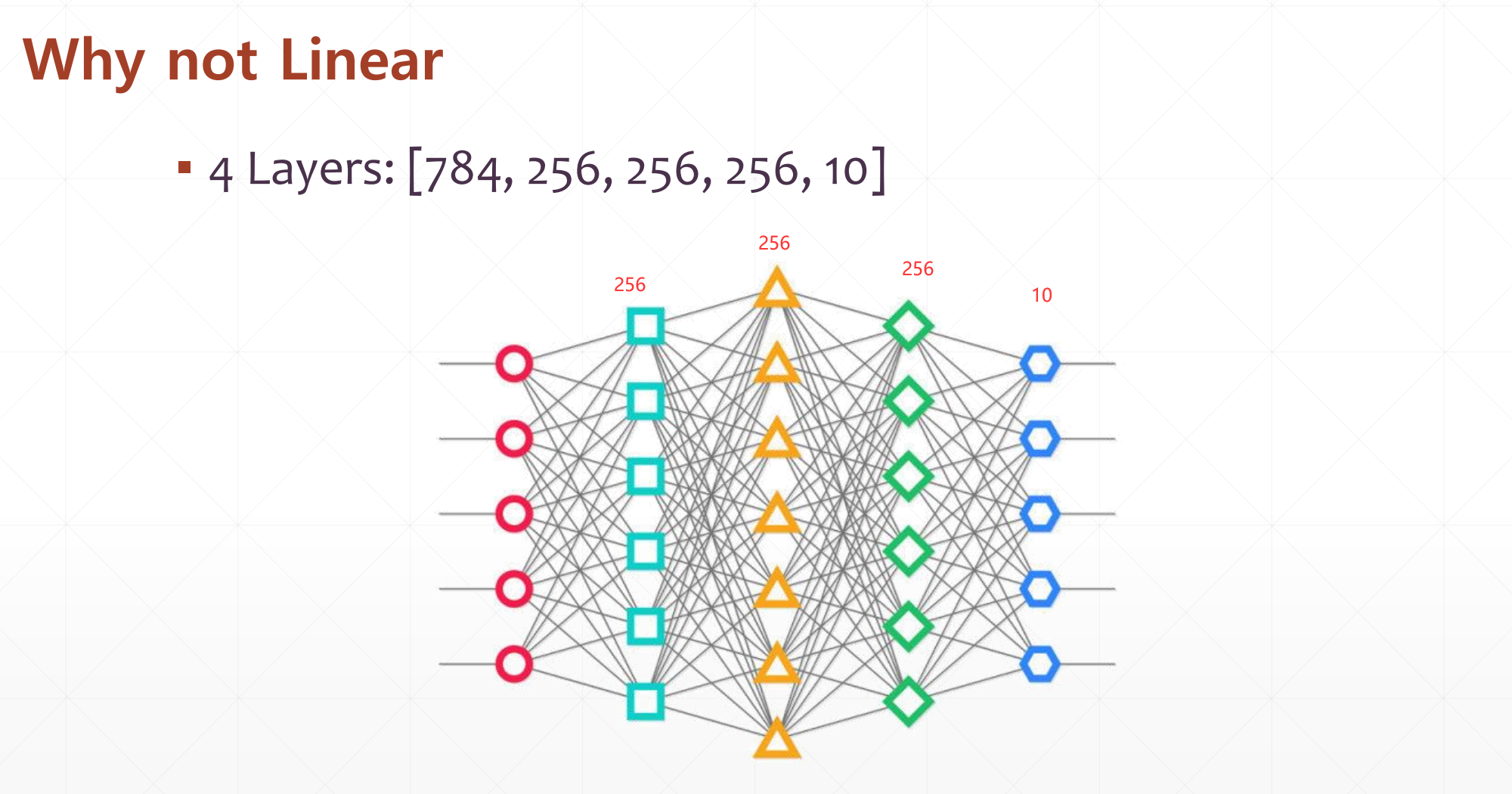
其每一层的参数个数：
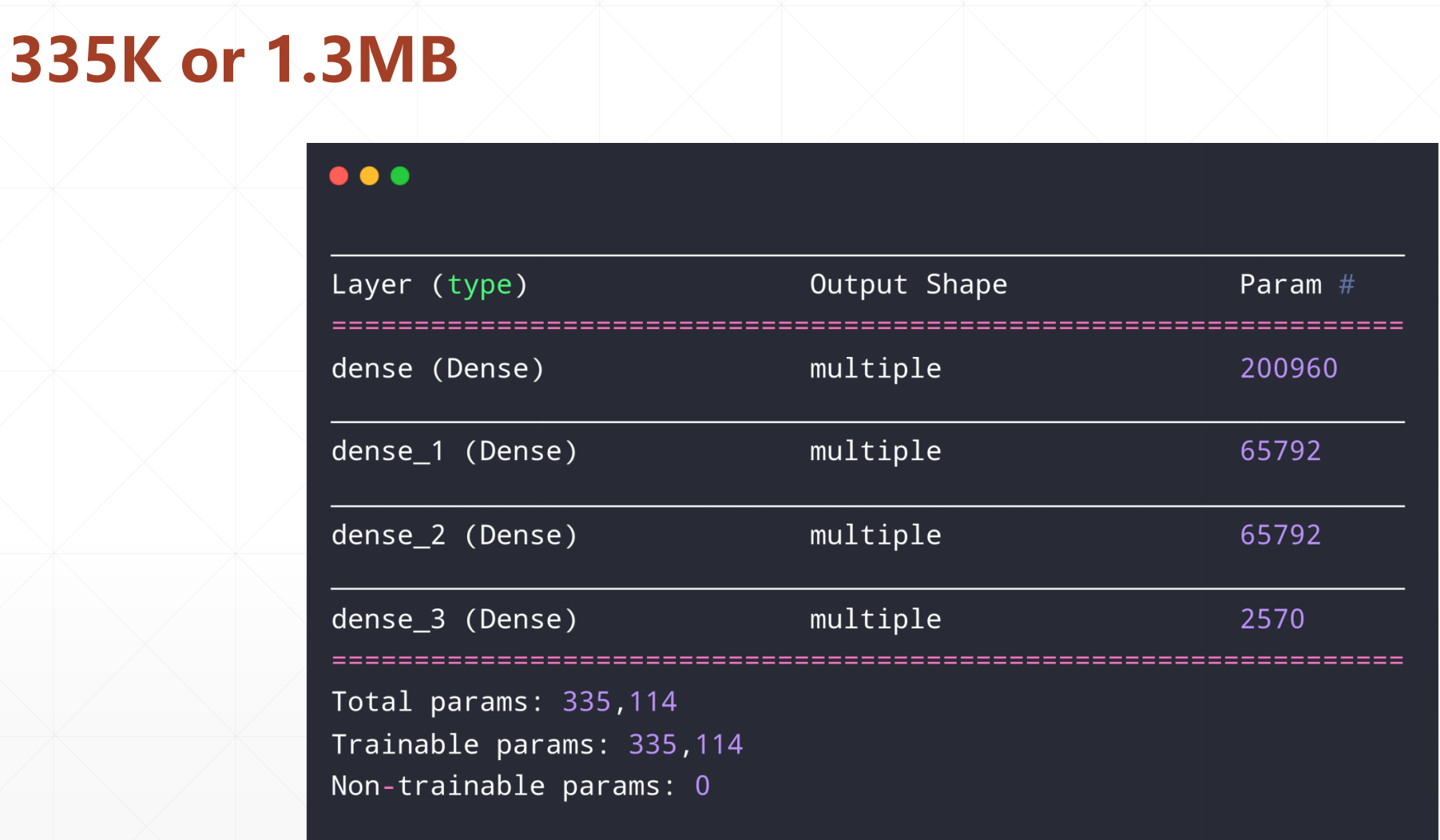
这里需要1.3M的存储空间。
但是在当时的年代：已经算很大了。
那怎么解决内存占用的问题呢？
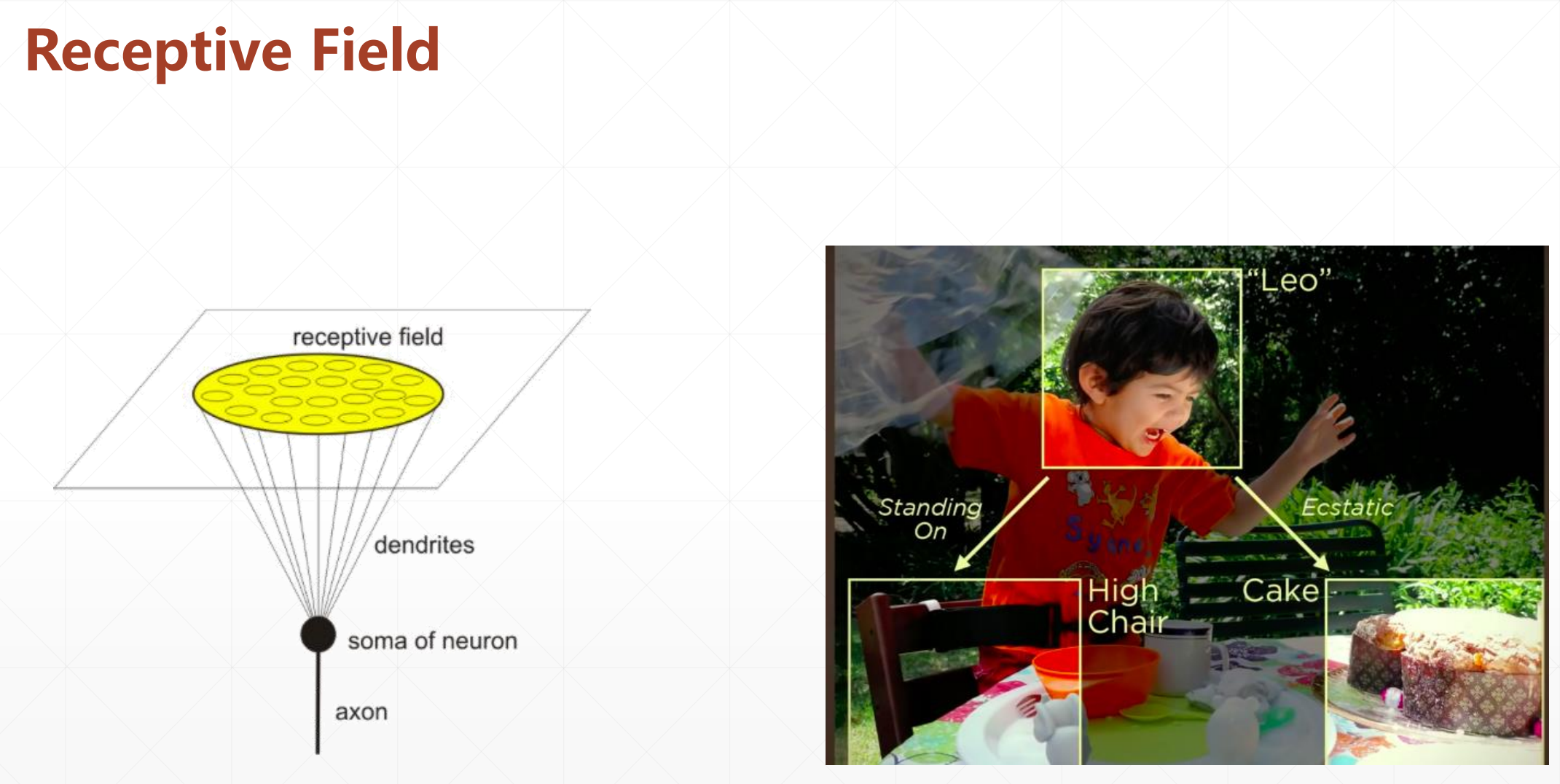
我们一眼看过去可能只是看到了局部。局部感知眼。
2 全连接神经网络VS局部连接神经网络
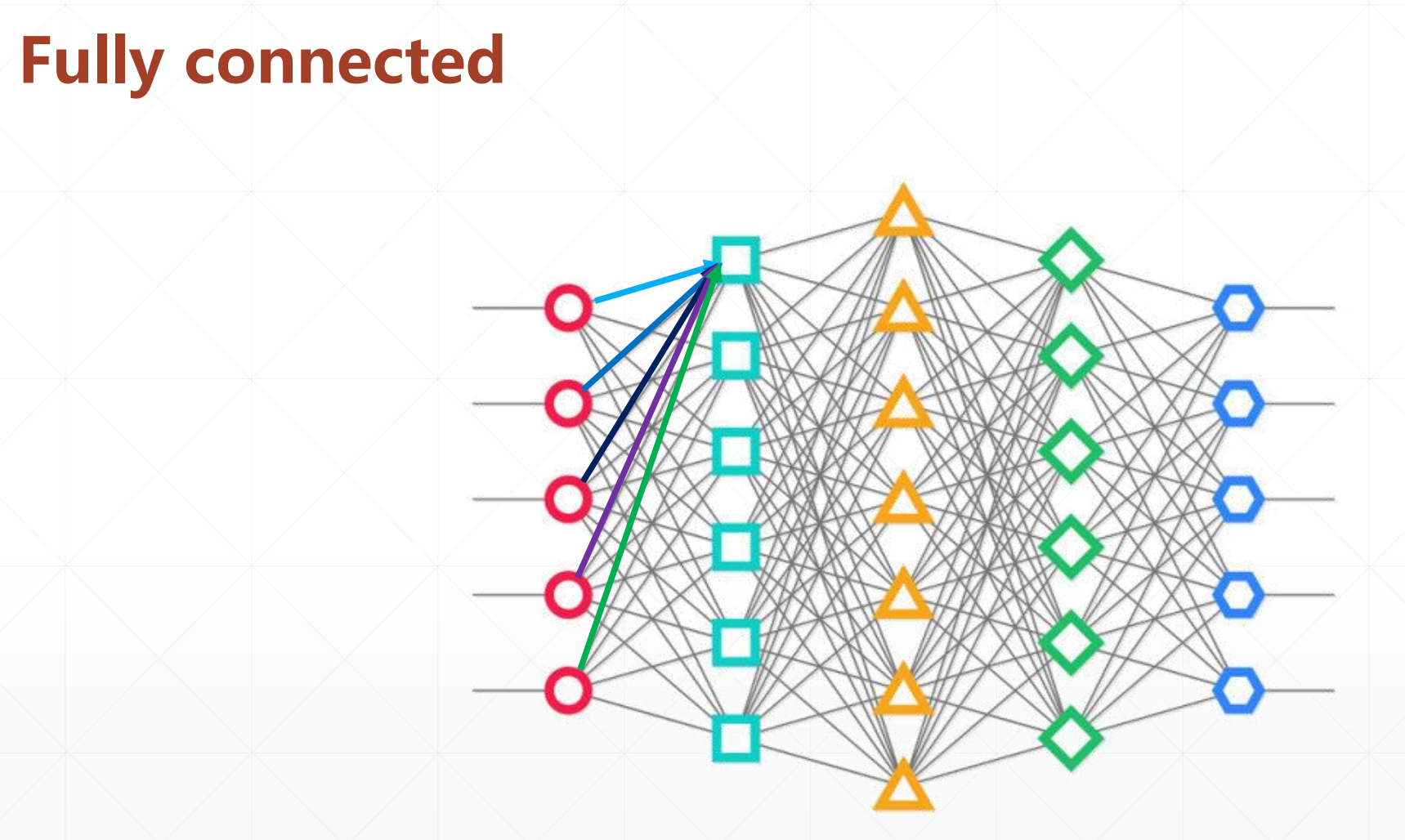
这是Fully connected：就是每个点都和其前面一个点全连接。
然后这是 partial connected：
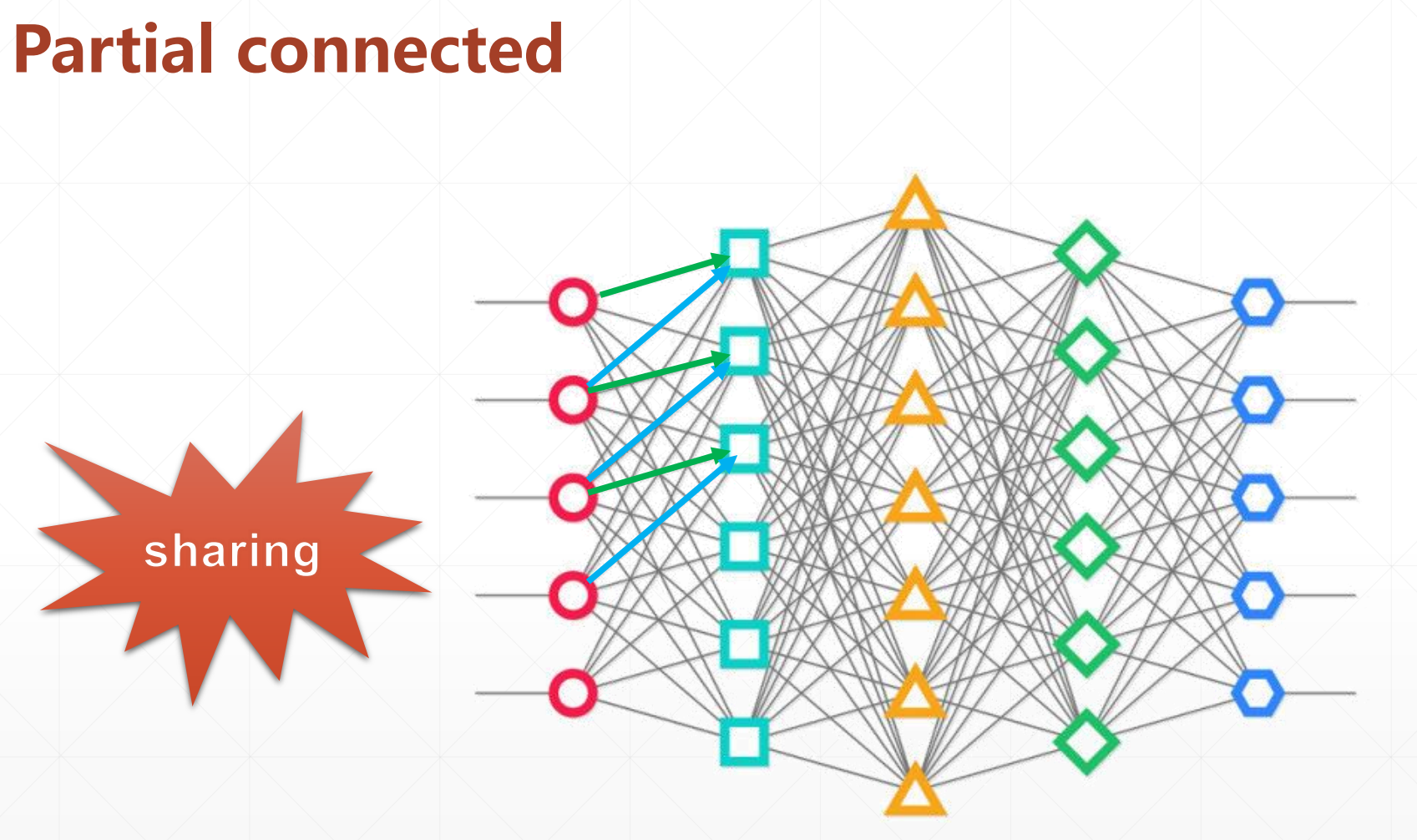
这里我们每一个点都只关注和我局部相关的点。在这里我们全部的绿色线都是一样的，全部的蓝色线都是一样的，所以我们这里只有两个参数。
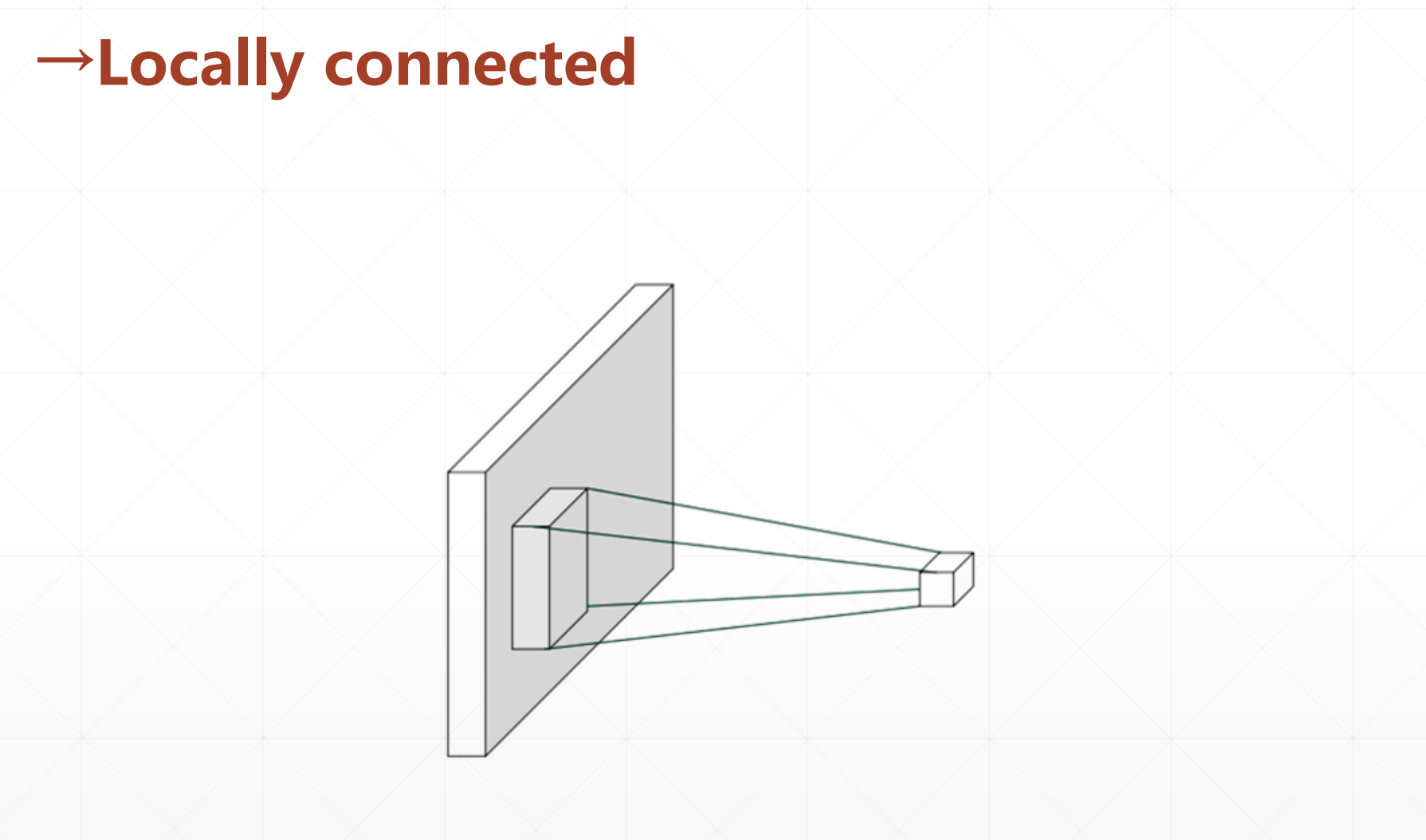
在这里我们每一层都使用同样的观察方式。
我们在这里和全局相连做个对比：
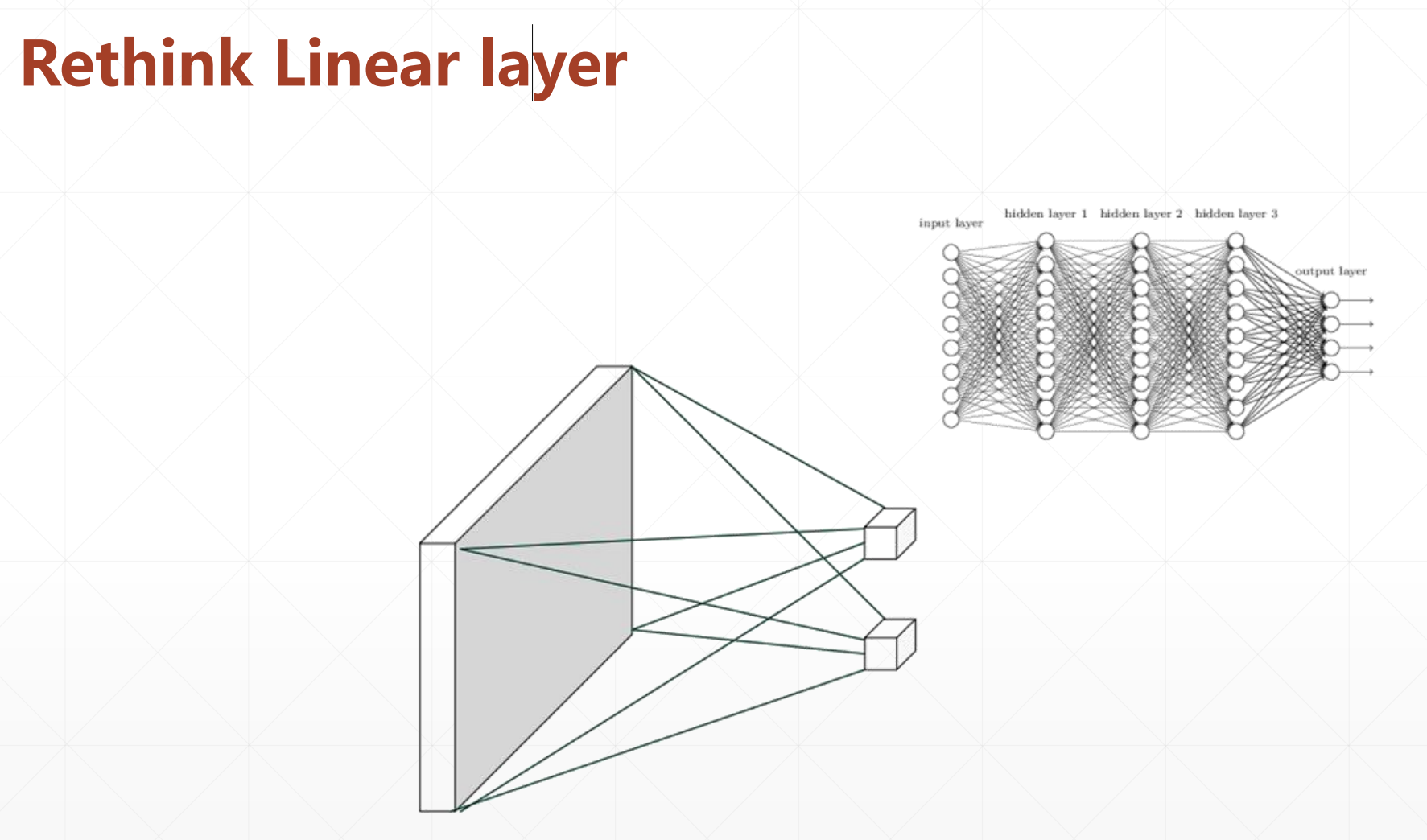
前面那个观察只是观察了局部。
举个例子：
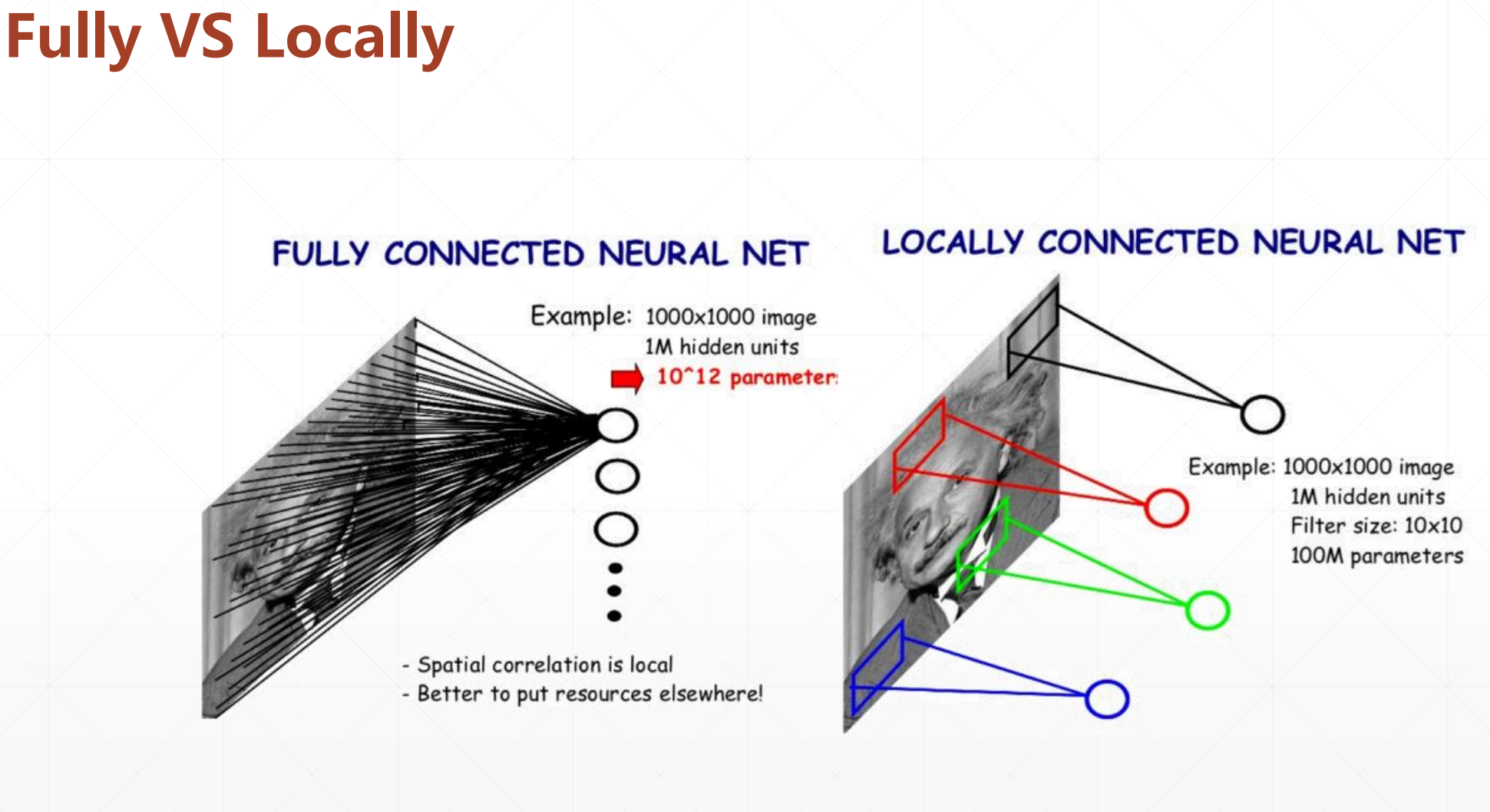
就上面的图片，如果我们用全连接的话，参数可能会达到10^12，但是我们用局部连接的话，可能只需要几百个就行。
他的过程：
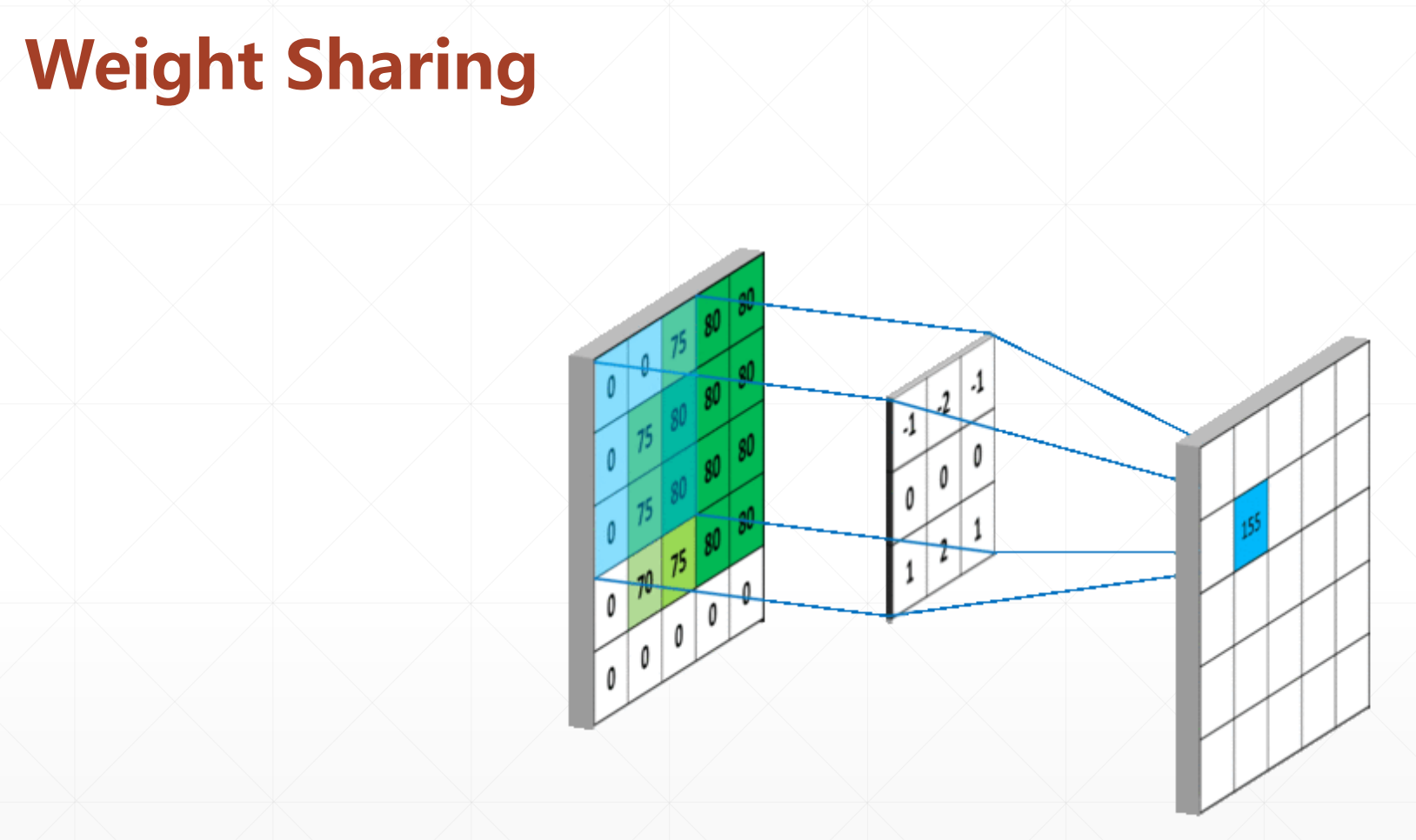
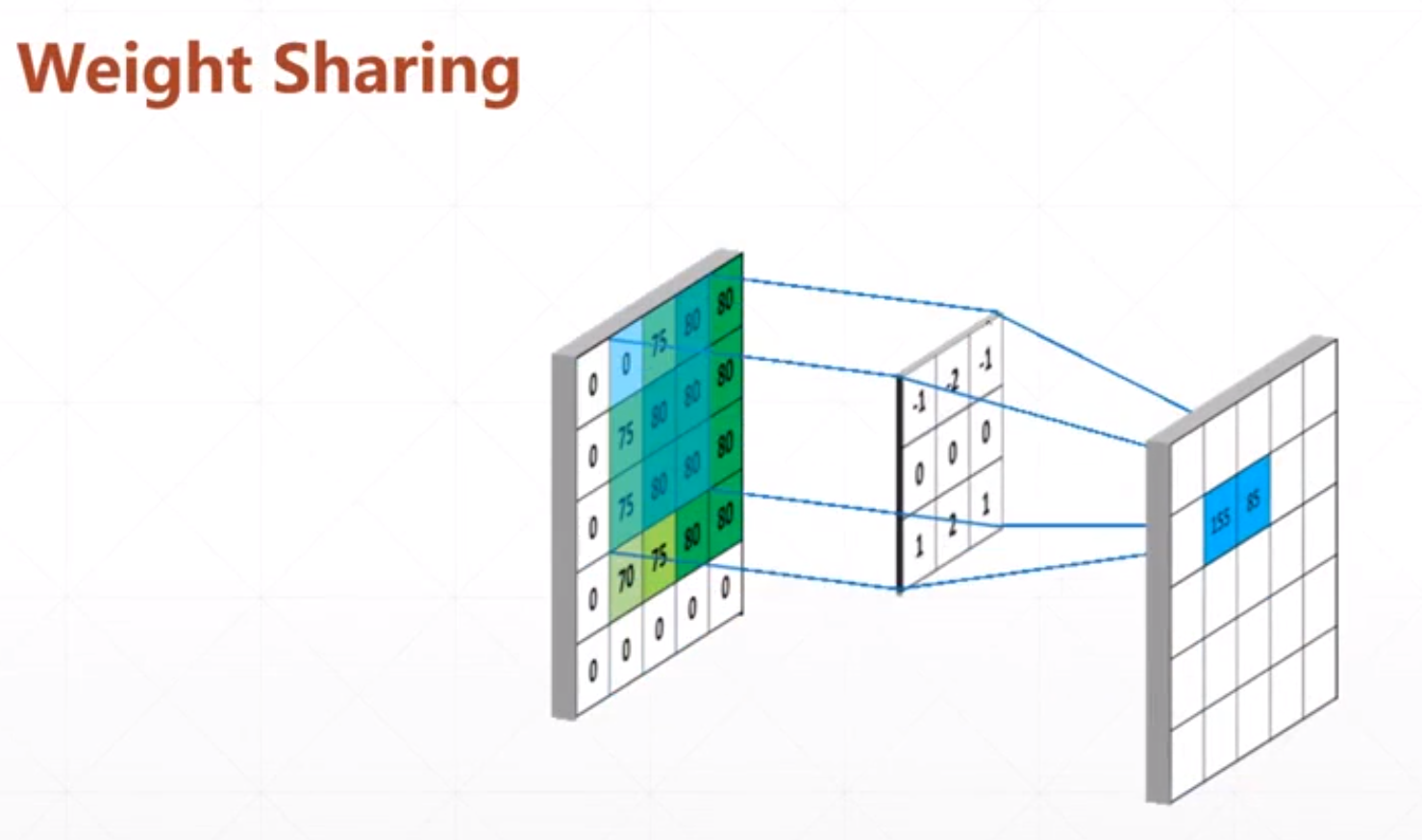
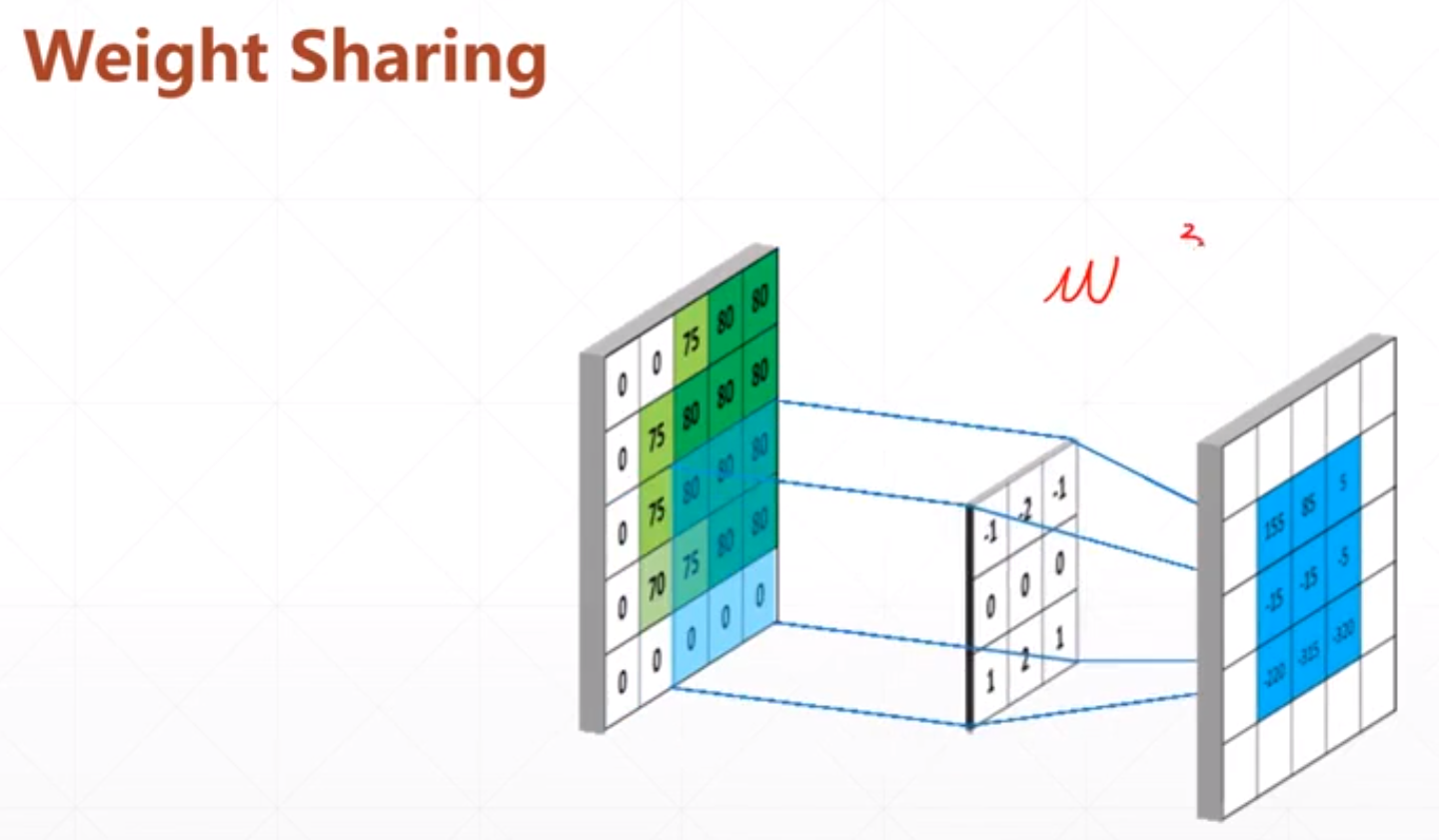
然后我们需要学习的参数只有3*3的参数。
如果我们输入有多个通道的时候：
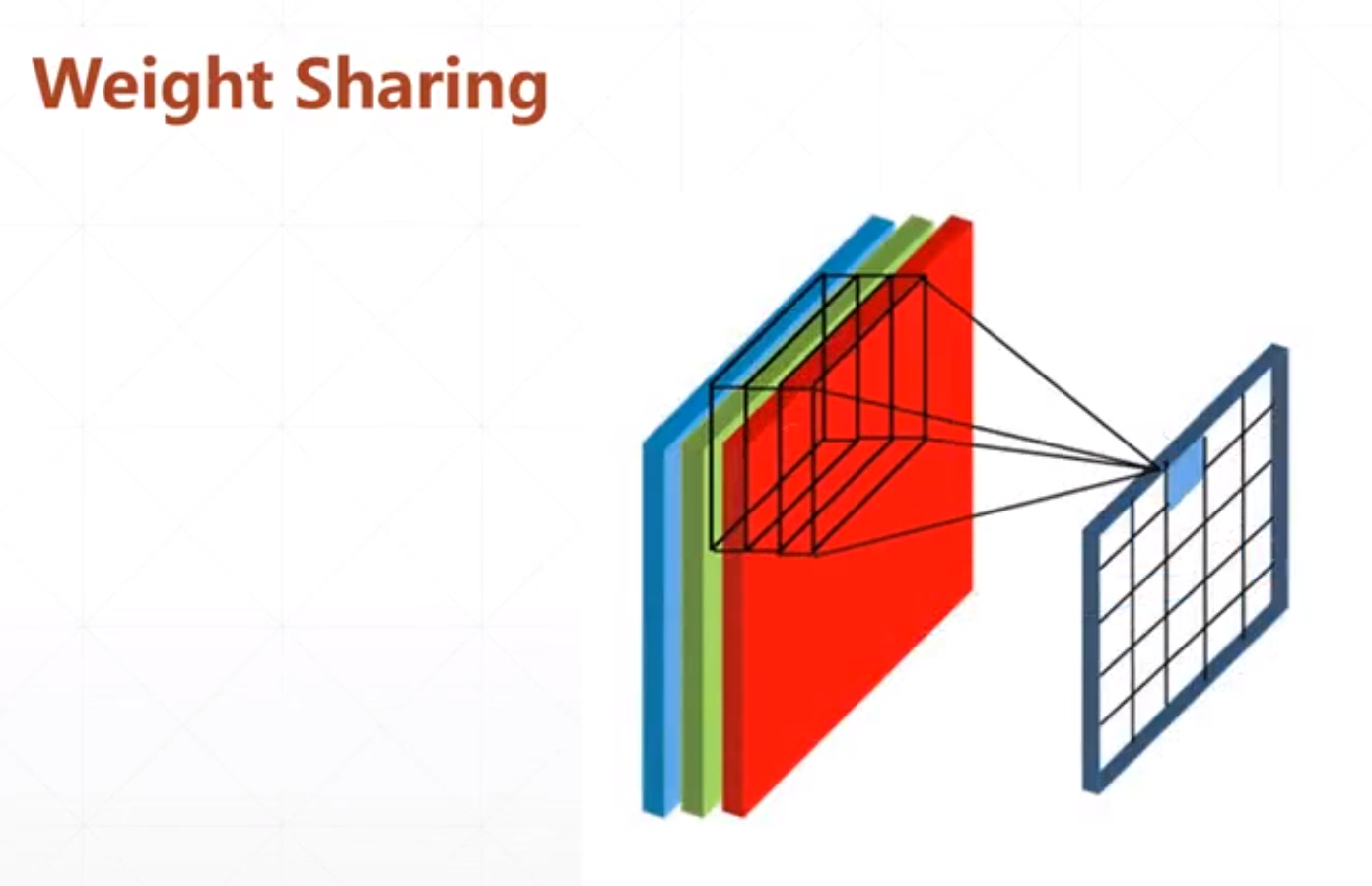
然后我们的参数也有多个通道，这个也需要多个矩阵。也是个三维的。
所以我们利用局部相关和权值共享的机制，大大减少了参数量。
我们这里怎么运算呢：
采用对应位置相乘在相加的策略。
3 什么叫卷积
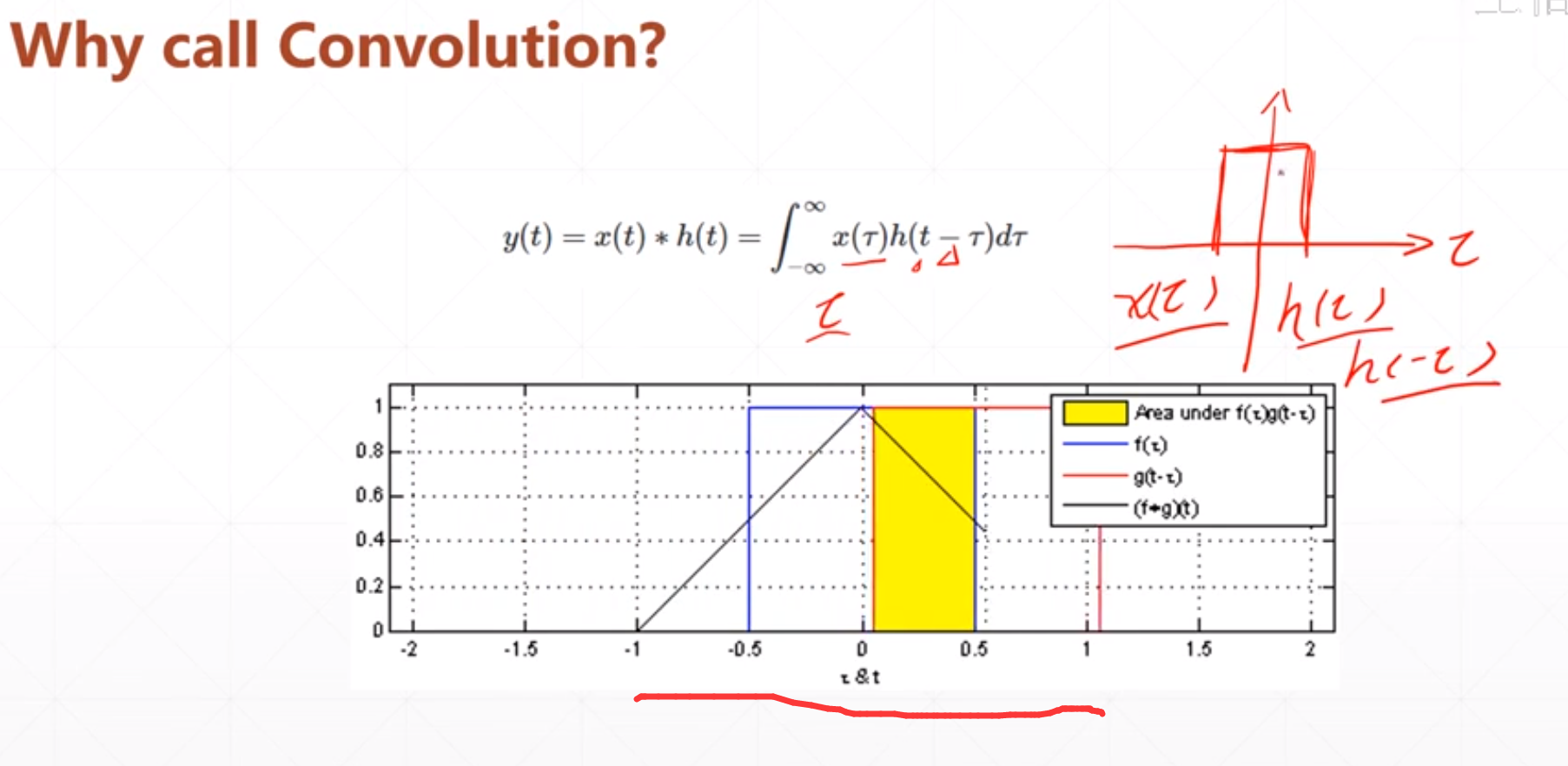
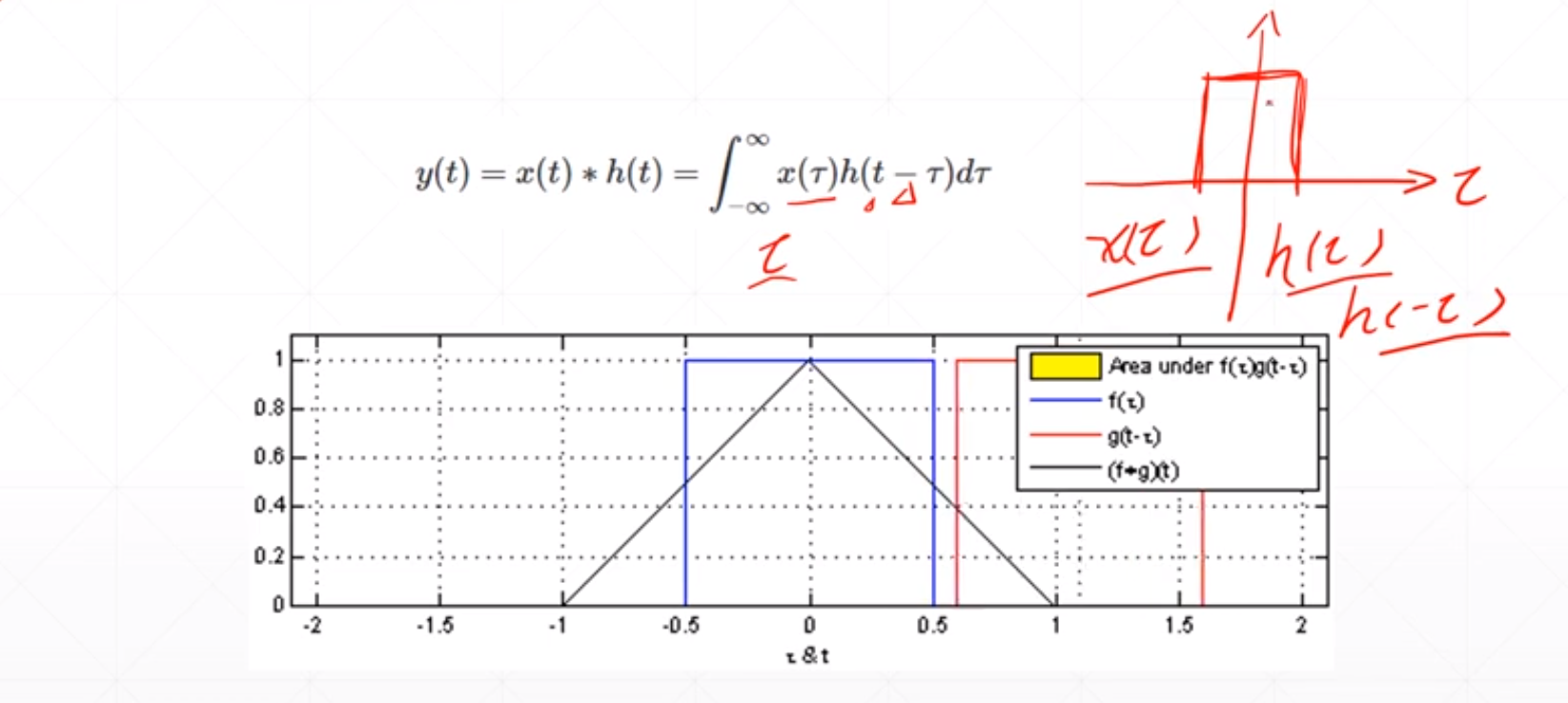
这个卷积就是连个信号进行镜像偏置之后再做一个积分。
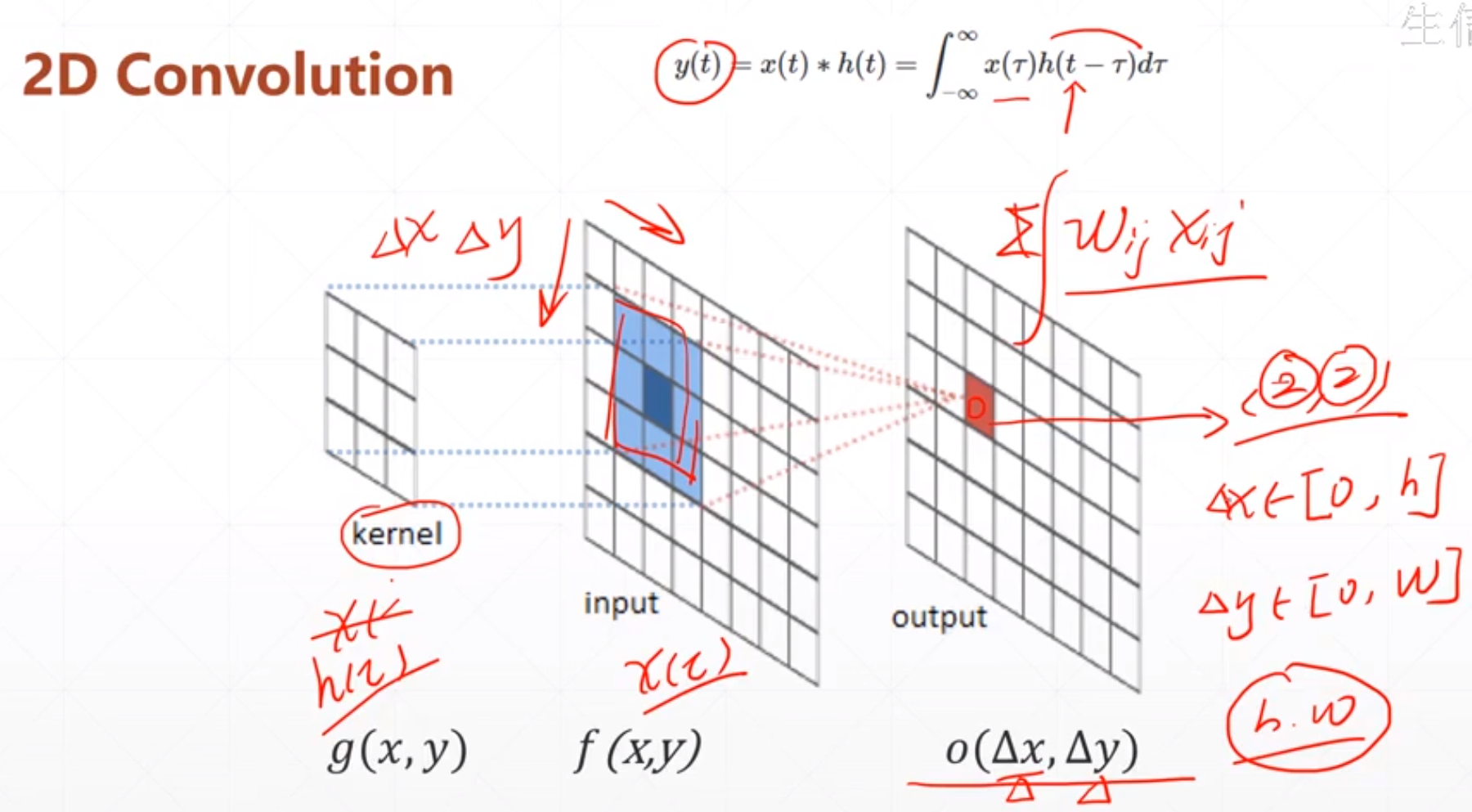
然后对这个图片数据进行卷积的时候，这个kernel是这个h()，然后input就是这个x()，然后卷积就是，这个kernel进行偏置之后再求相乘，这里的积分就看成了相加。
我们为什么要用一个卷积操作呢？
我们用这个卷积核之后发现图片会变得更加sharpen
这样之后会变得更加模糊。
然后是边缘检测：
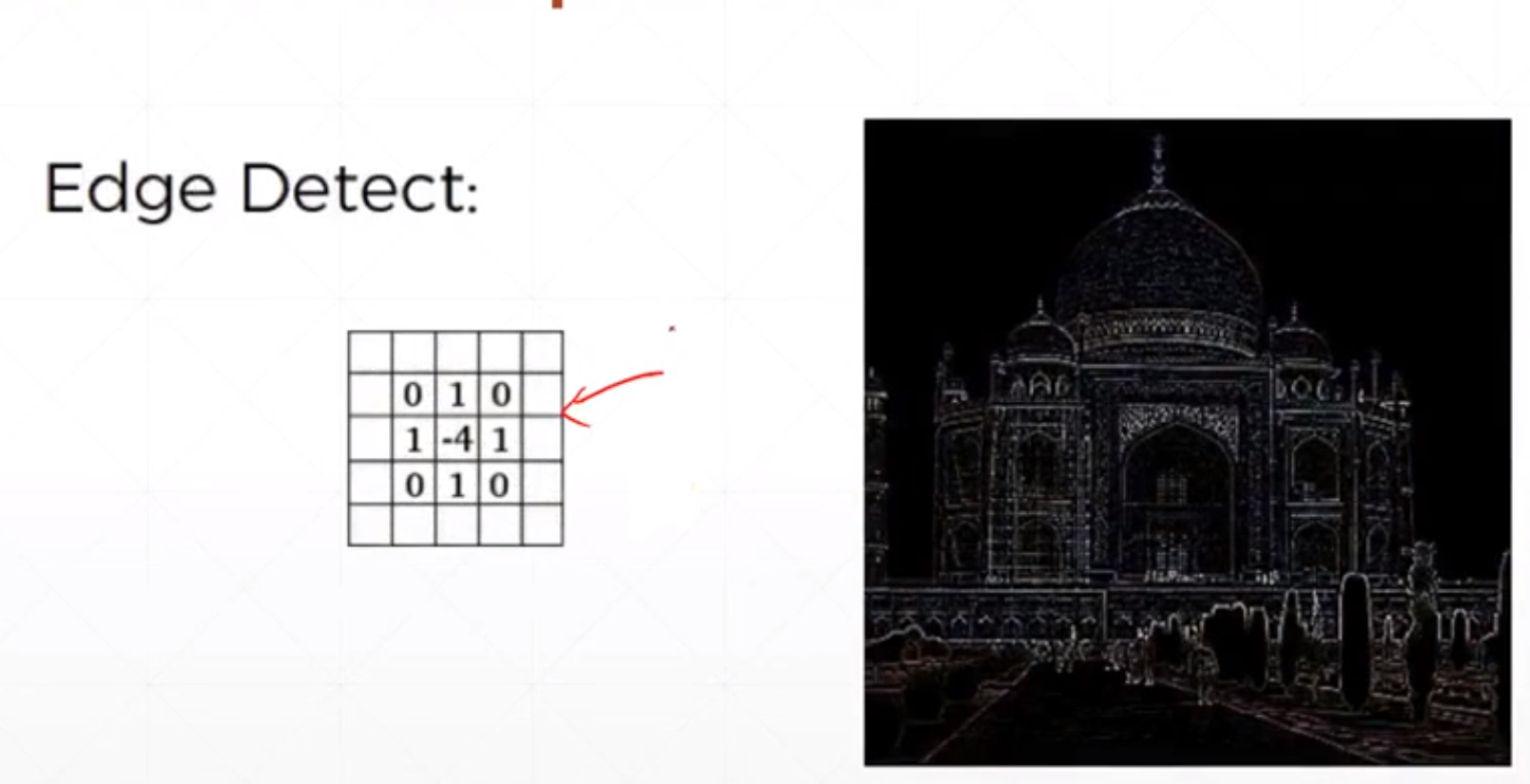
对于不同的卷积核，可能卷积出来的不同。
4 卷积神经网络
再上面的2D Convolution中
全局共享和滑动窗口
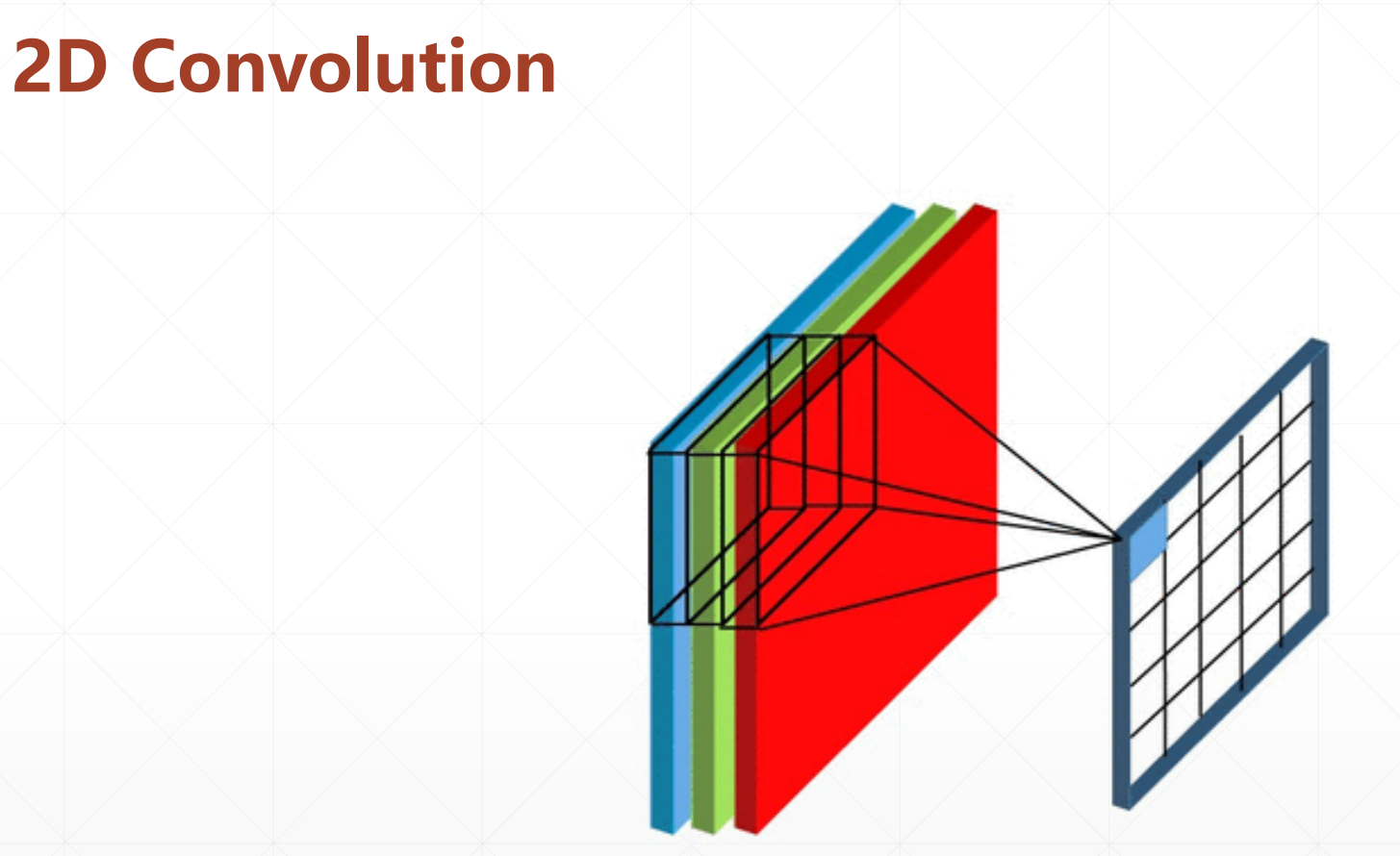
4.1 单通道kernel
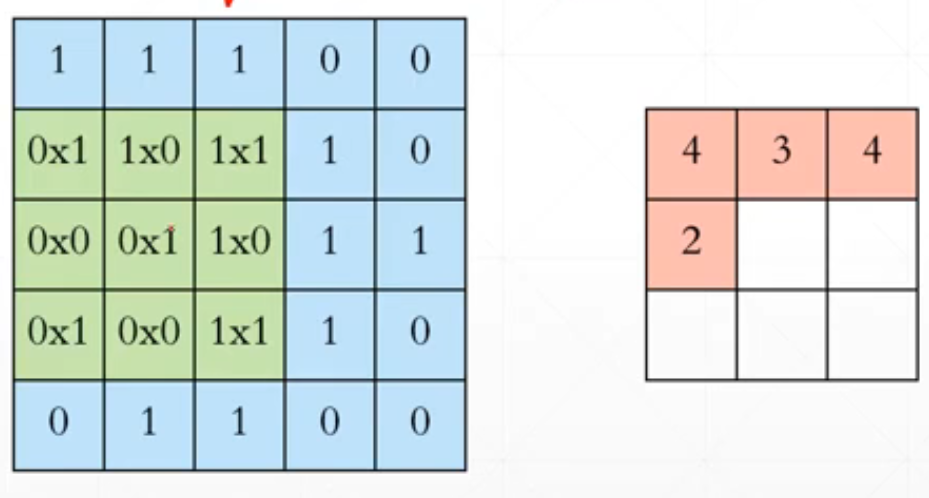
input选用[b,5,5,1]=
[[1,1,1,0,0],
[0,1,1,1,0],
[0,0,1,1,1],
[0,0,1,1,0],
[0,1,1,0,0]]。
然后我们的w=
[[1,0,1],
[0,1,0],
[1,0,1]]
.......
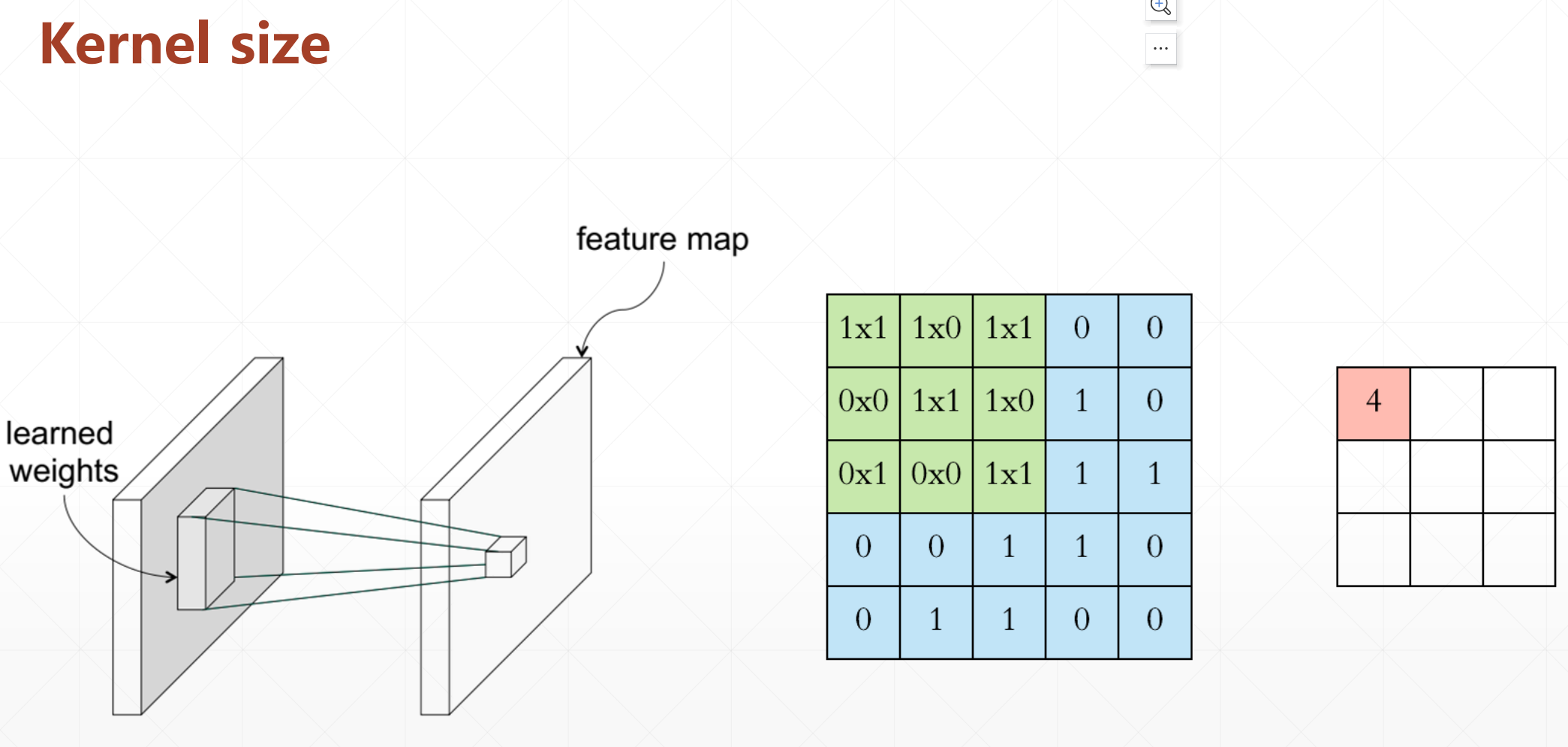
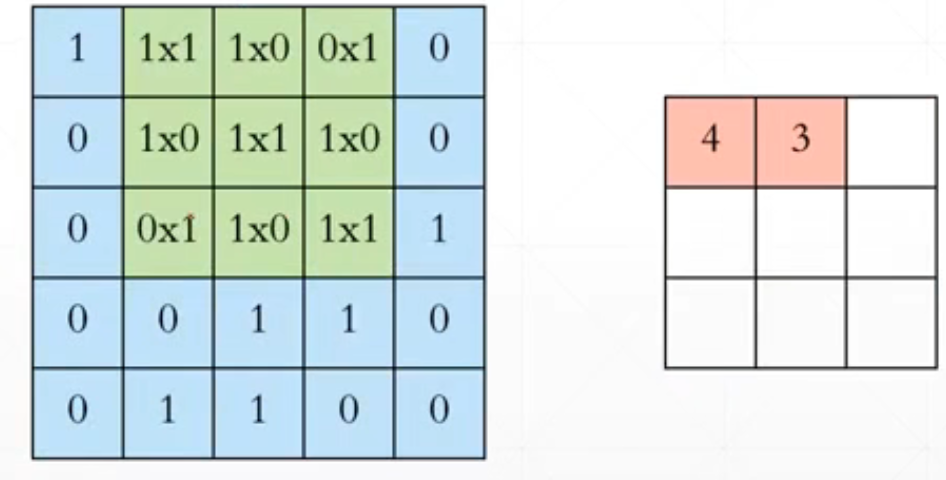
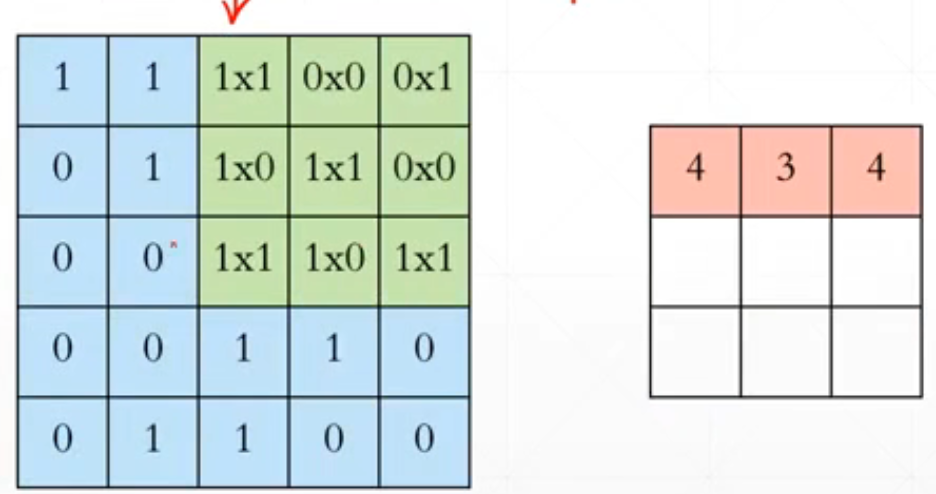
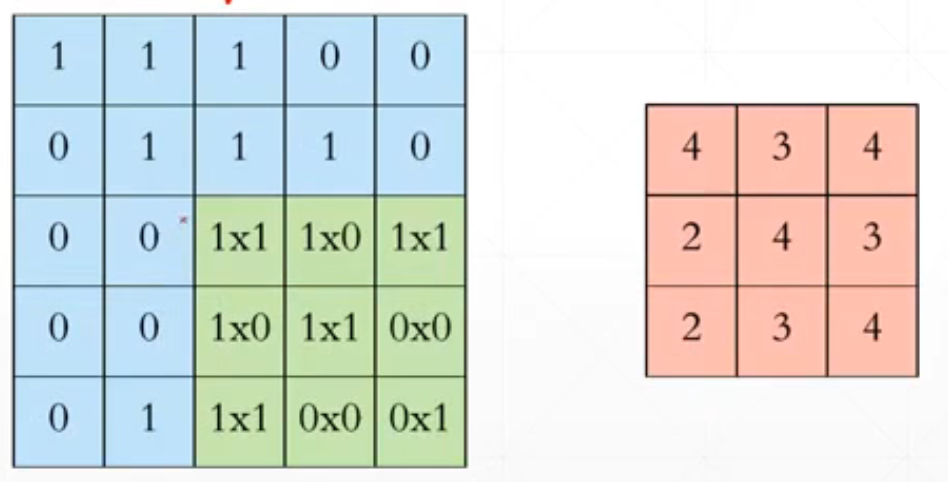
对应位置相乘再相加。然后经过一个变化之后从[b,5,5,1]->[b,3,3,1]。
4.2 多通道kernel
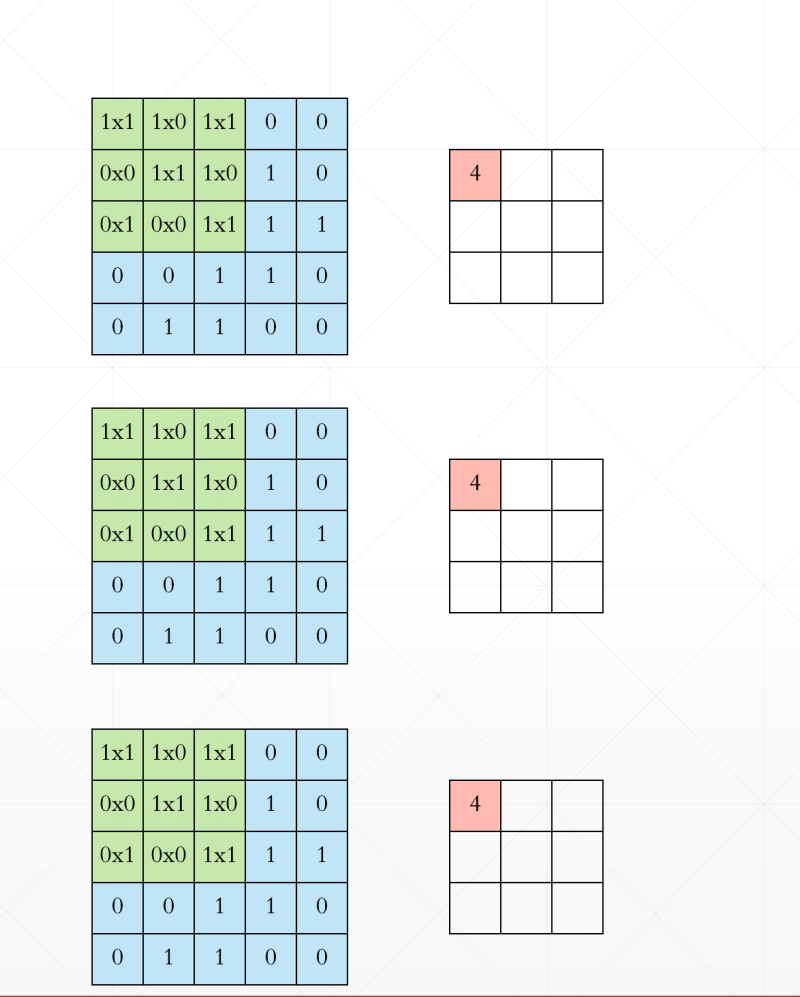
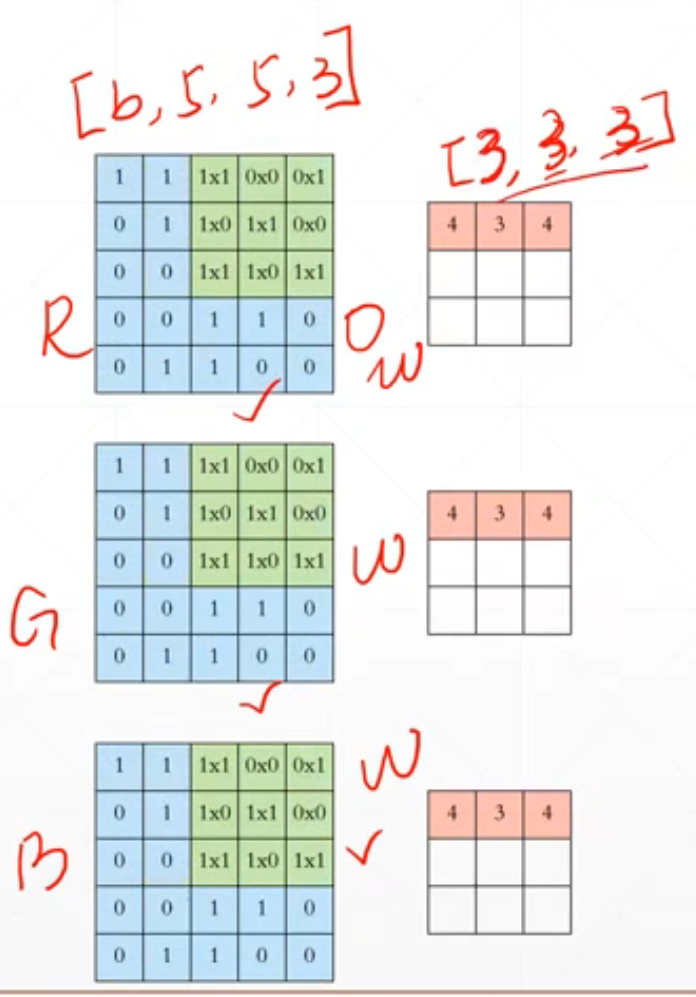
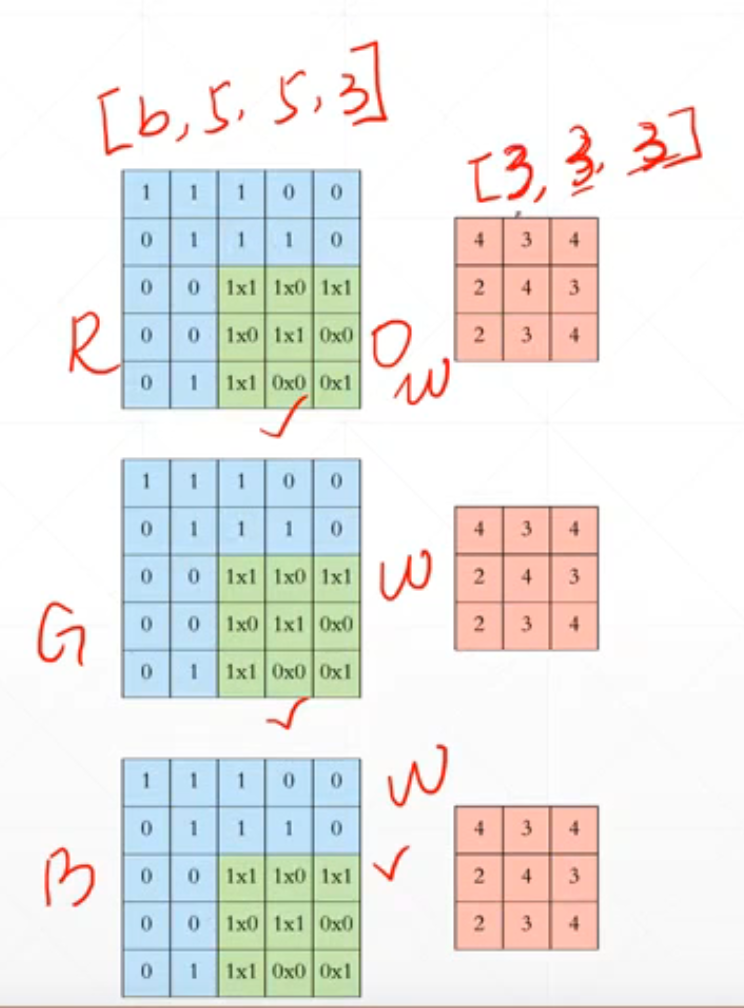
再这里我们有三个通道，所以这里我们[b,5,5,3]对应的kernel就是[3,3,3]。
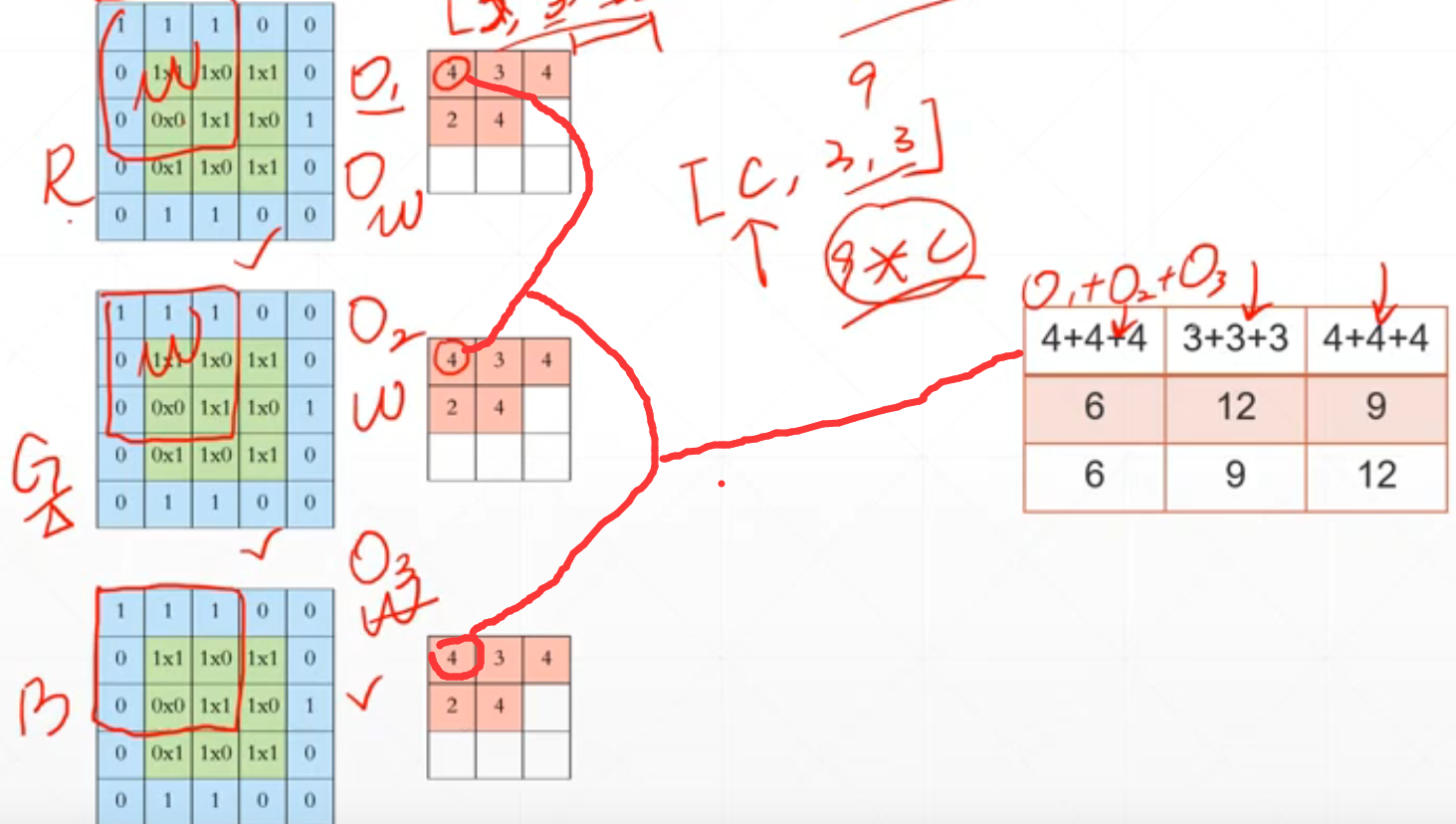
如果我们有c个通道的话，就是[b,5,5,c]通过kernel[c,3,3]将数据融合为[b,3*3]。这里我们就变成了[b,9]。这里我们对应的数据融合后的[b,9]中的对应位置就是\(O_1\)+\(O_2\)+\(O_2\)。
就是就是通过kernel加工后的对应位置的中每个位置相加。
所以我们的[b,h,w,c]=>[b,h',w',1]（h'<h,w'<w）。
4.3 Padding & Stride
4.3.1 padding
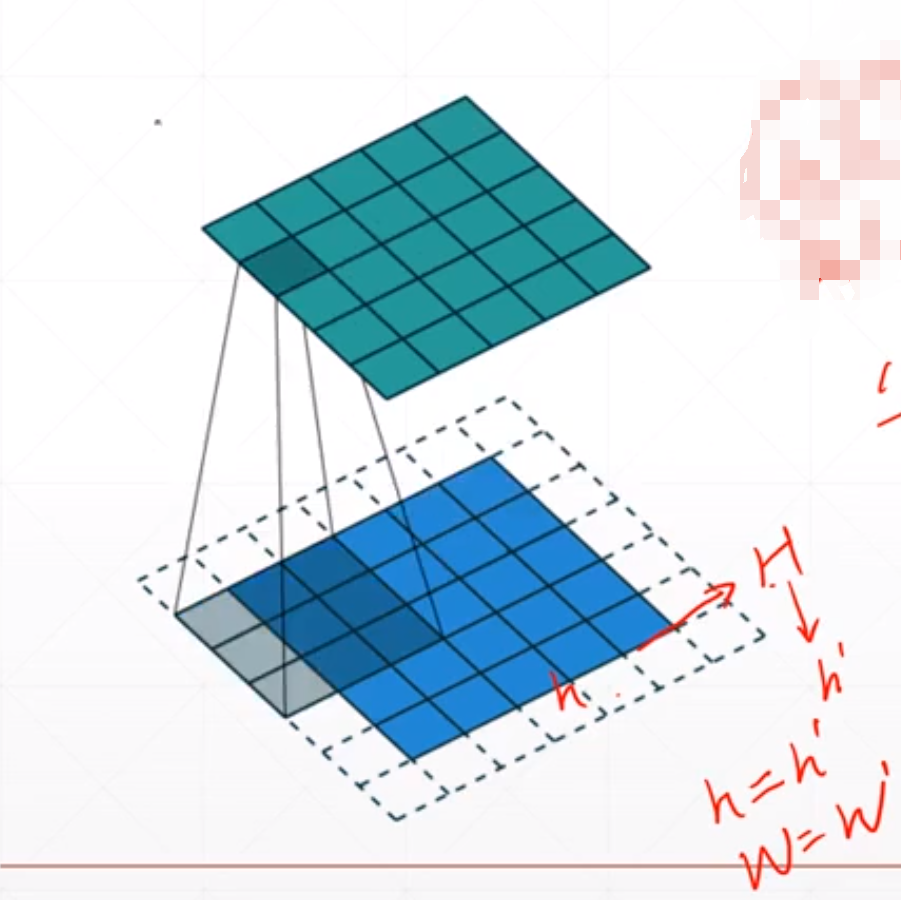
有时候我们可能需要h'=h,这里我们可以通过padding来控制。这个就是我们我们可以通过padding使得h=>H，然后我们再对这个H进行kernel变成h'。就是我们可以增大这个h。
4.3.2 Stride
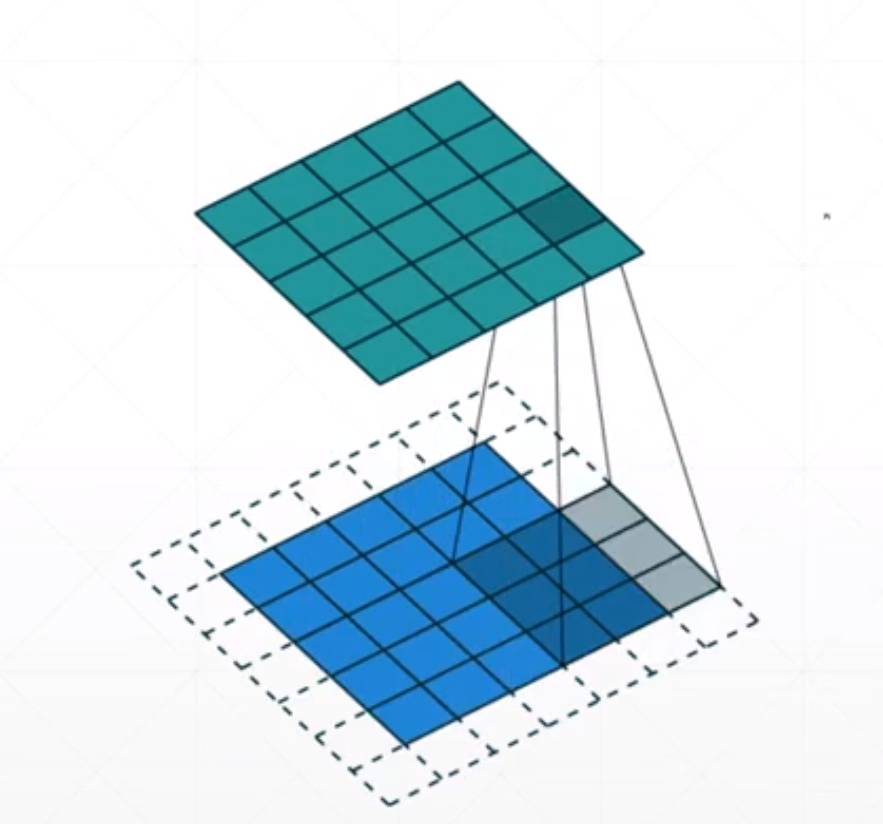
对于上面的我们每次都是向下和向右移动一小格。我们可以通过控制使得它每次移动两小格。所以我们的输出就会减少。
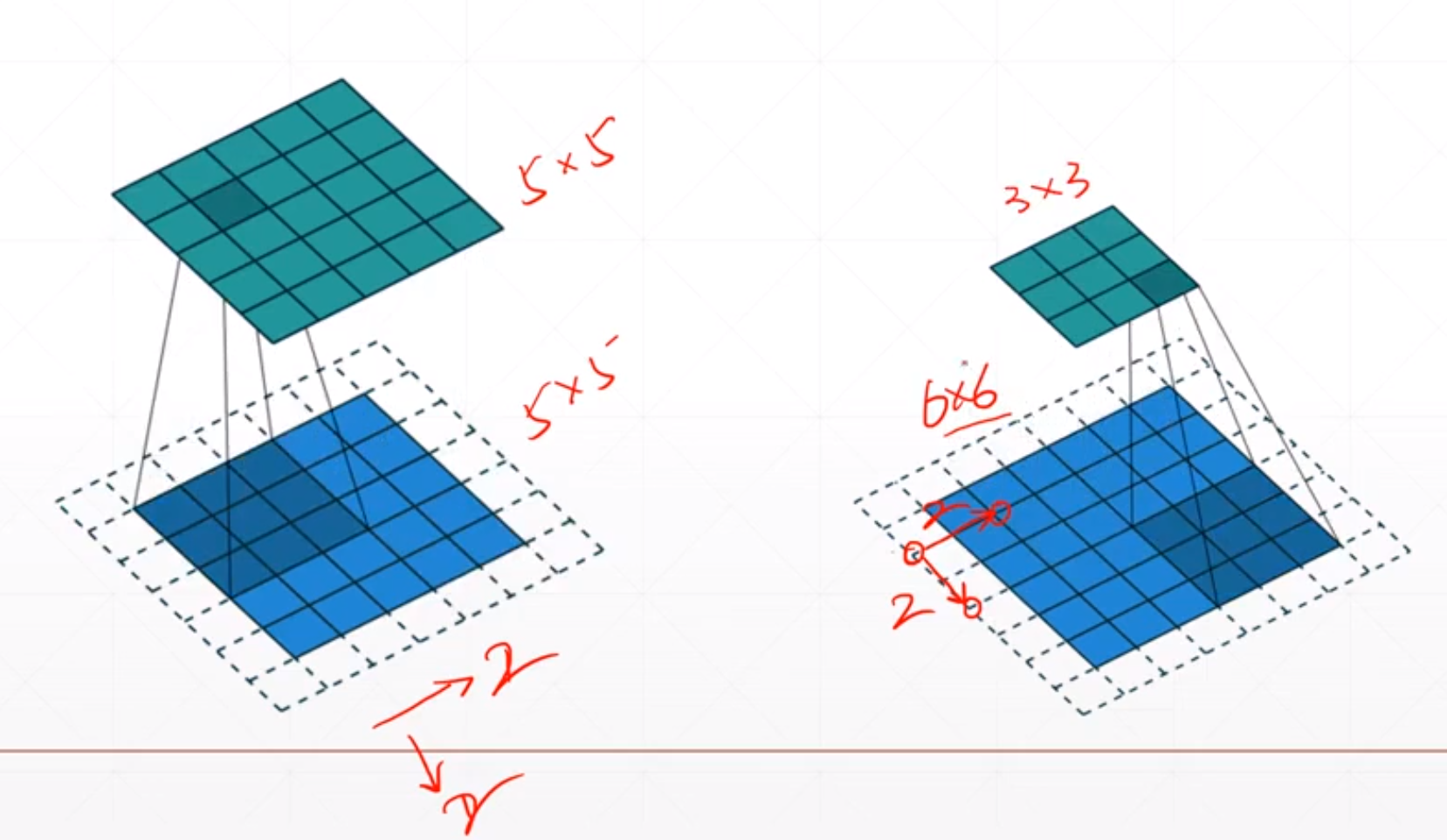
对于上面的例子，我们如果步长为1的时候我们[5,5]=>[5,5]。如果步长为2的时候就变成了[3,3]。我们可以通过这个stride参数进行降维的操作。
我们可以通过调节padding和stride 来调节output的h'和w'。我们可以通过调整我们的padding和stride来使得我们输出的shape是我们想要的。
4.3.3 Channels
我们在做多通道操作时,我们的[b,5,5,c]通过[c,3,3]会变成[b,3,3,1]，这里的channel变成了1，变成了单通道的。但是有时候我们希望不是单通道的，而是channel变多一点，就是3->120->256->512。也就是我们希望我们的h',w'变少，c变多，但是我们通道[c,3,3]只能是我们的channel变成1。
这里我们引入核的概念，这里我们把一个[c,3,3]叫做一个核的话。那么我们就是一个卷积核[c,3,3]就会使得变成[b,3,3,1]。所以我们如果有N个卷积核的话，就是[N,c,3,3]变成[3,3,N]。所以我们的[b,5,5,c]=>[b,3,3,N]，前提是我们有一个[N,C,3,3]的卷积核。这里的N就叫咱N个卷积核。然后C就是input-C。这里的N和你想变成的通道相联系，C和你输入的有关系。
例如：
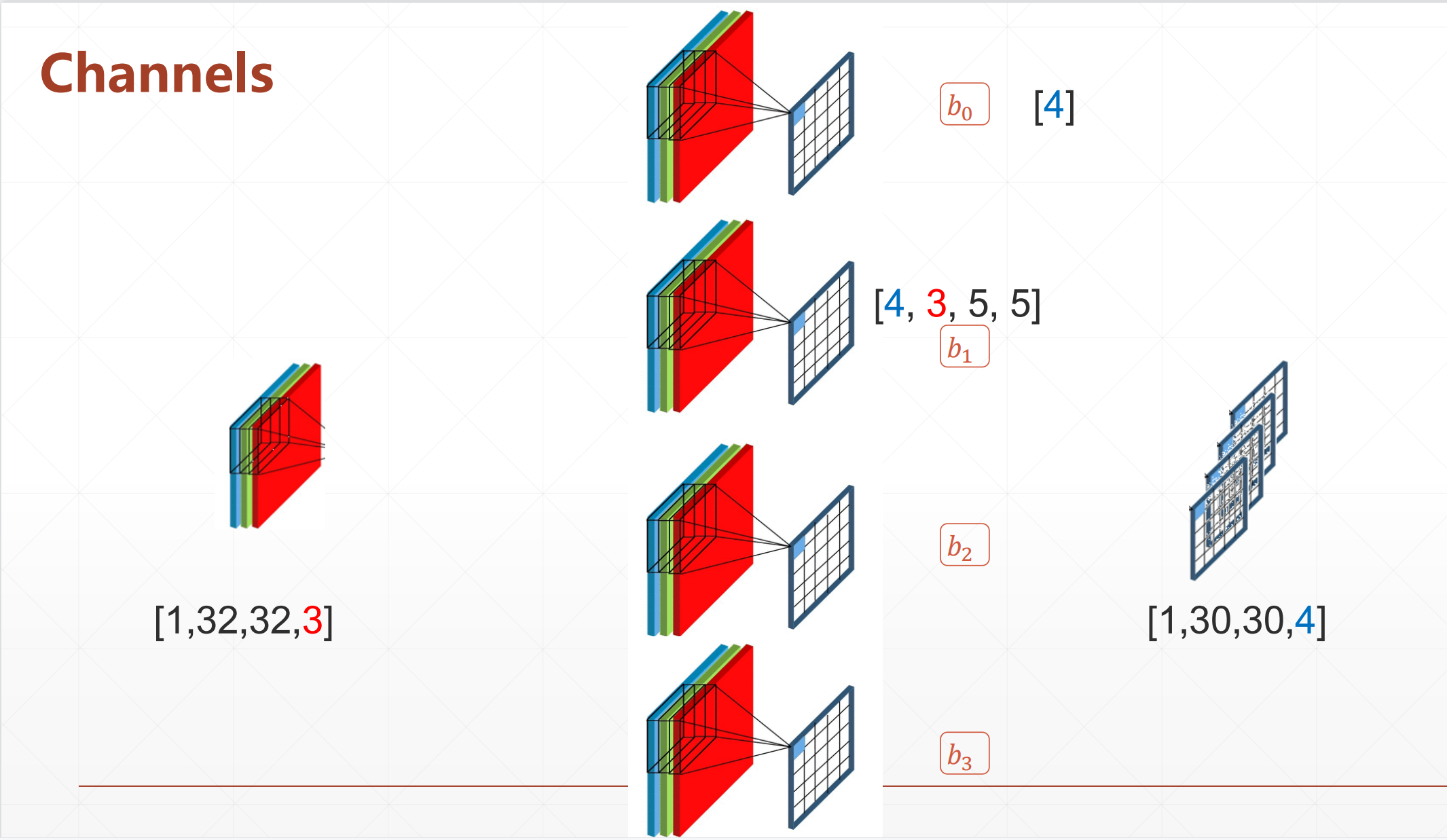
我们输入的是一个[1,32,32,3]的通道。如果我们还是使用[3,3,3]的通道的话，我们会得到一个[30,30,1]的output。但是我们如果想变成多个通道的话，我们就是增加多个卷积核。如图我们就变成了一个[1,30,30,4]。我们这里话需要加一个b取决于我们的输出的channels数量，就是b[4]。
对于下面这个例子：
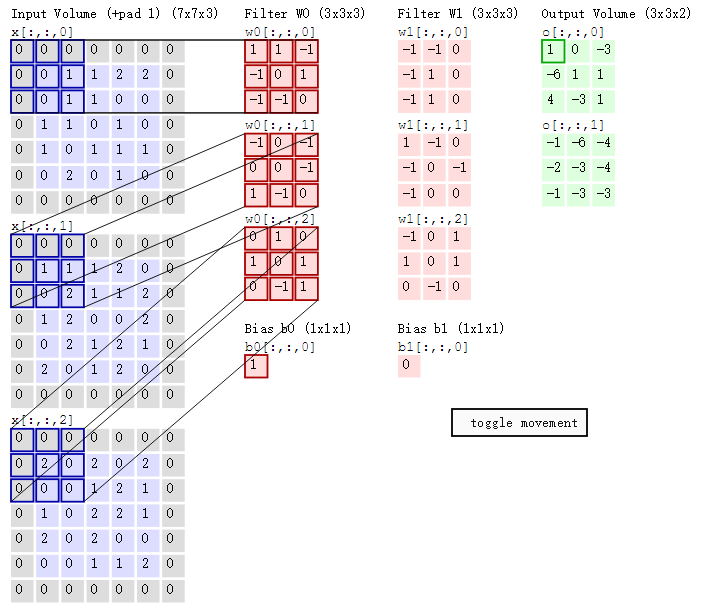
即上图中的输出结果1具体是怎么计算得到的呢？其实，类似wx+b，w对应滤波器Filter w0，x对应不同的数据窗口，b对应Bias b0，相当于滤波器Filter w0与一个个数据窗口相乘再求和后，最后加上Bias b0得到输出结果1，如下过程所示：
对于这个例子：
这个Input:[b,32,32,3]，w:[4,3,5,5],b:[4],output:[b,30,30,4]，
这个input中的3是指的有三个通道，所以这个w中的第二个数要是3,然后我们这三个通道的每一个卷积核对应位置
相乘相加之后是三个数\(o_1\),\(o_2\),\(o_3\)。然后我们这个三个数相加之后才是这个output中对应的一个数。如果我们output想有4个通道的话，这个w哪里也得有4个[3,5,5]的卷积核，就对应了b是4个数,然后每个卷积核再算output的时候都加上对用的b[i]。
然后这个padding可以在你的output上打0这样的补丁，使得你的输出的h',w'增加，然后这个Stride可以使得你的h',w'成倍的减小。
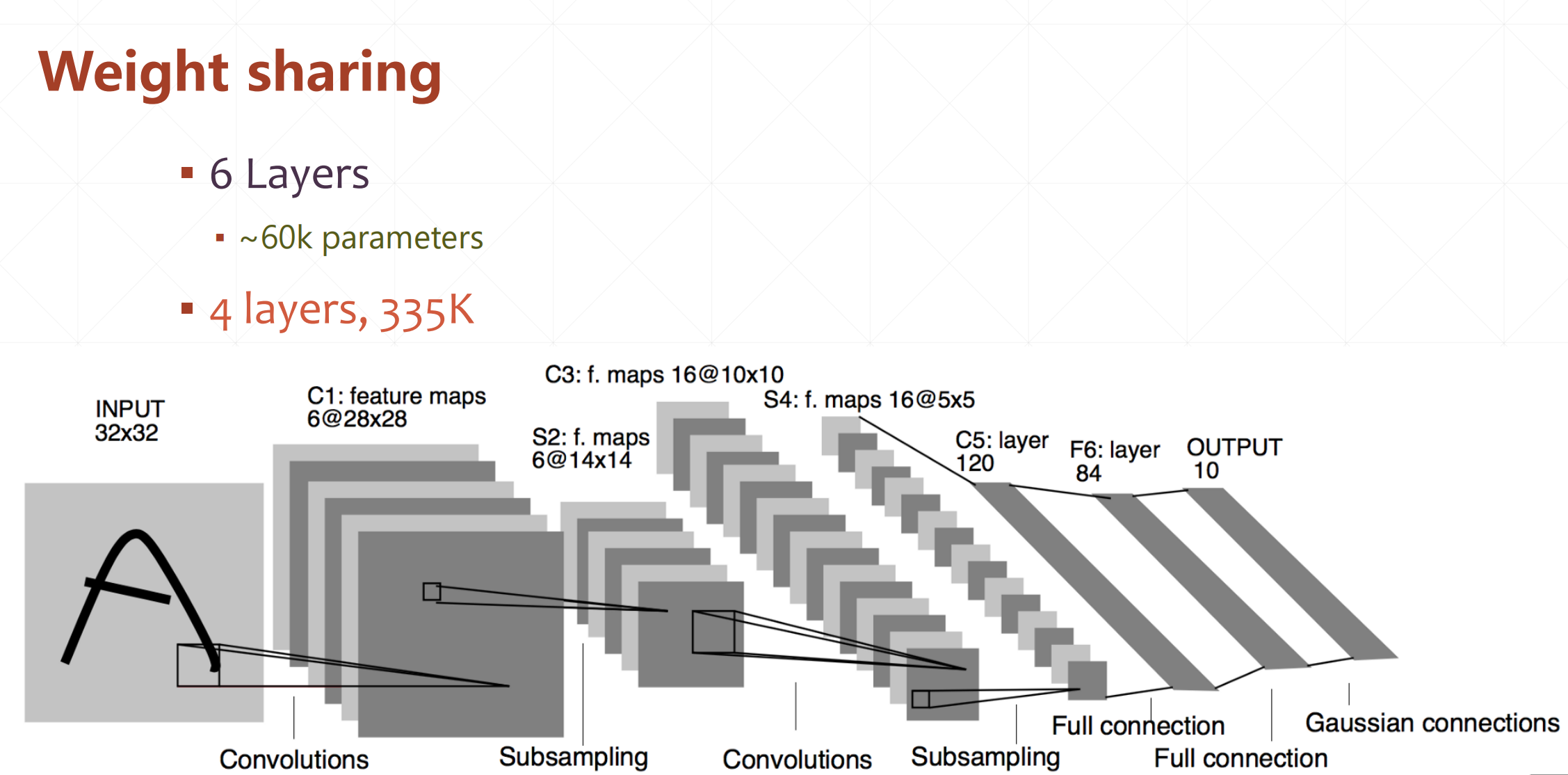
5 LetNet
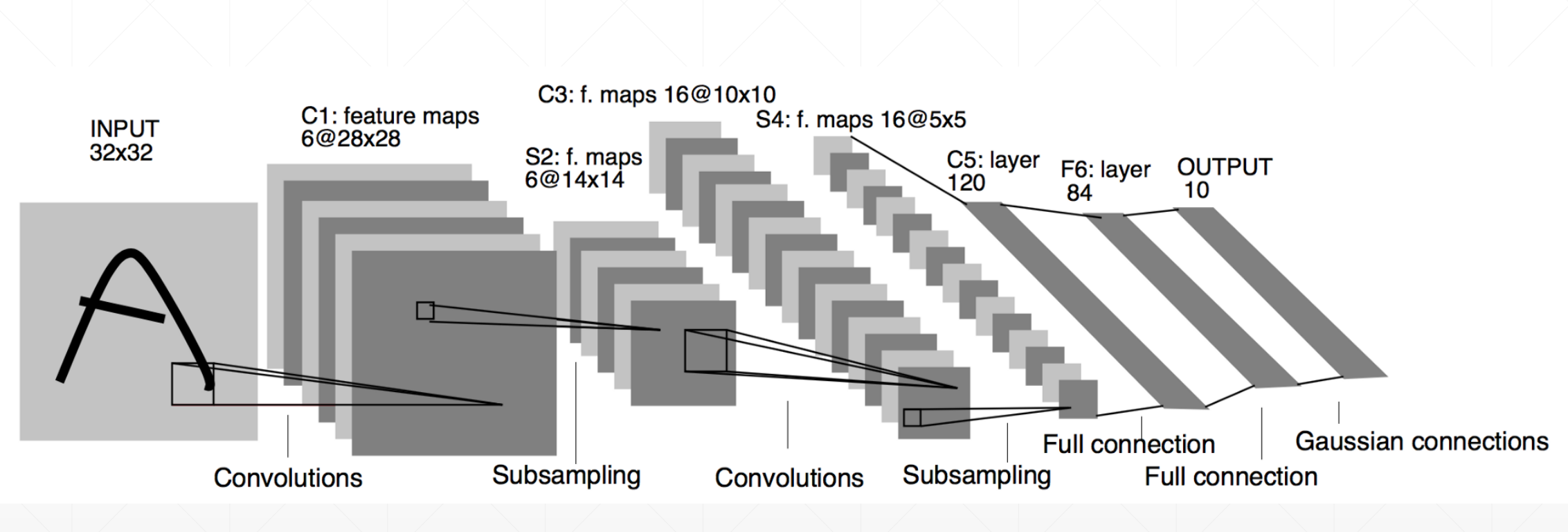
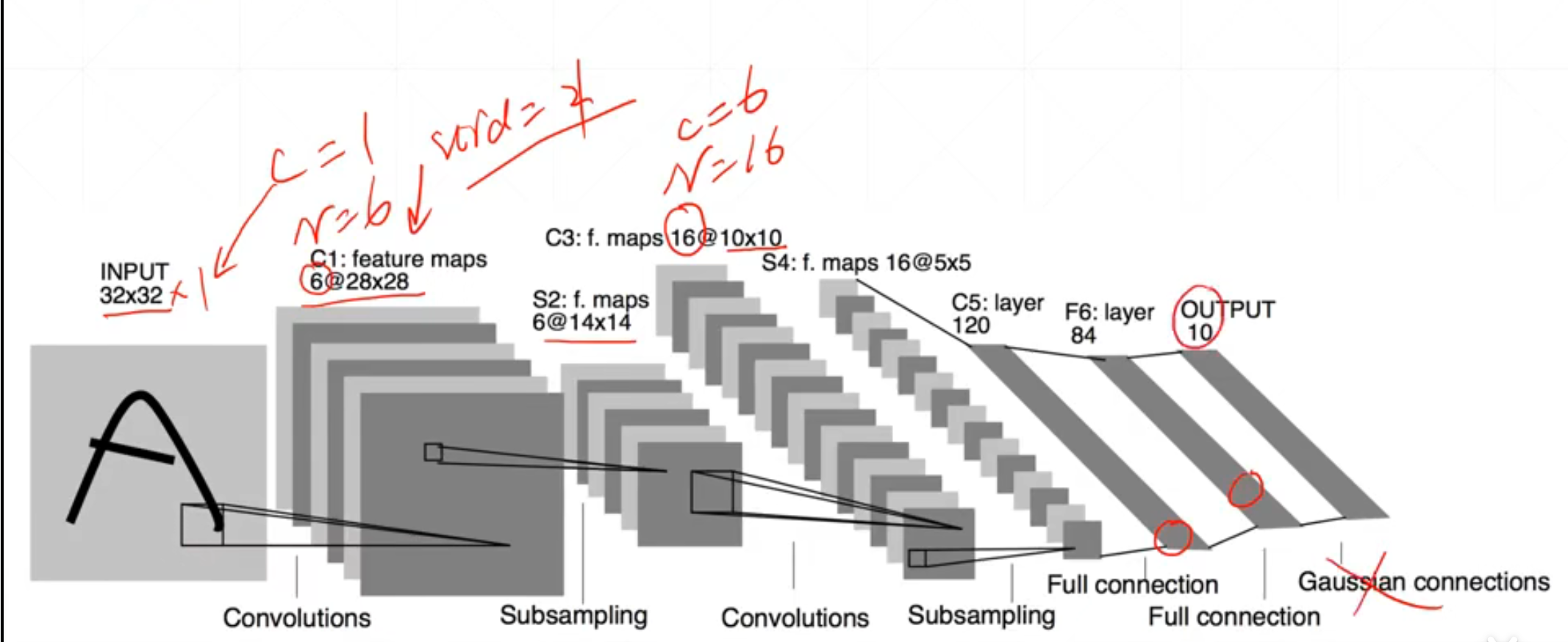
我们会发现都是一些convolutions之后subsampling的堆叠，这样有什么好处呢？
这里我们通过c+s可以就像搭积木一样，可以实现从底层特征的抽取到高层特征的过程。
6 tensorflow实现一个简单的convolutions层(layers.Conv2D)
这里的API：
Conv2D(filters, kernel_size, strides, padding, activation=‘relu’, input_shape)
filters: 过滤器数量(也就是卷积核的个数)
kernel_size: 指定（方形）卷积核窗口的高和宽的数字
strides: 卷积步长, 默认为 1
padding: 卷积如何处理边缘。选项包括 'valid' 和 'same'。默认为 'valid',valid输出的h'和w'小于h,w。但是same输出的大于h,w。
activation: 激活函数，通常设为 relu。如果未指定任何值，则不应用任何激活函数。强烈建议你向网络中的每个卷积层添加一个 ReLU 激活函数。
input_shape: 指定输入层的高度，宽度和深度的元组。当卷积层作为模型第一层时，必须提供此参数，否则不需要。
这个input_shape在第一层是需要的，否则不需要。
示例一：构建一个CNN，输入层接受的是 200×200 像素的灰度图片；输入层后面是卷积层，具有 16 个过滤器，宽高分别为 2；在进行卷积操作时，我希望过滤器每次跳转 2 个像素。并且，不希望过滤器超出图片界限之外，就是说，不用0填充图片。
Conv2D(filters=16, kernel_size=2, strides=2, activation='relu', input_shape=(200, 200, 1))
示例2：在示例1卷积层后再增加一层卷积层。新的卷积层有 32 个过滤器，每个的宽高都是 3。在进行卷积操作时，希望过滤器每次移动1个像素。并且希望卷积层查看上一层级的所有区域，因此，不介意在进行卷积操作时是否超过上一层级的边缘。
Conv2D(filters=32, kernel_size=3, padding='same', activation='relu')
示例3：简化写法。创建具有 64 个过滤器，每个的过滤器大小是 2×2。层级具有 ReLU 激活函数。卷积操作每次移动一个像素。并且丢弃边缘像素。
Conv2D(64, (2,2), activation='relu')
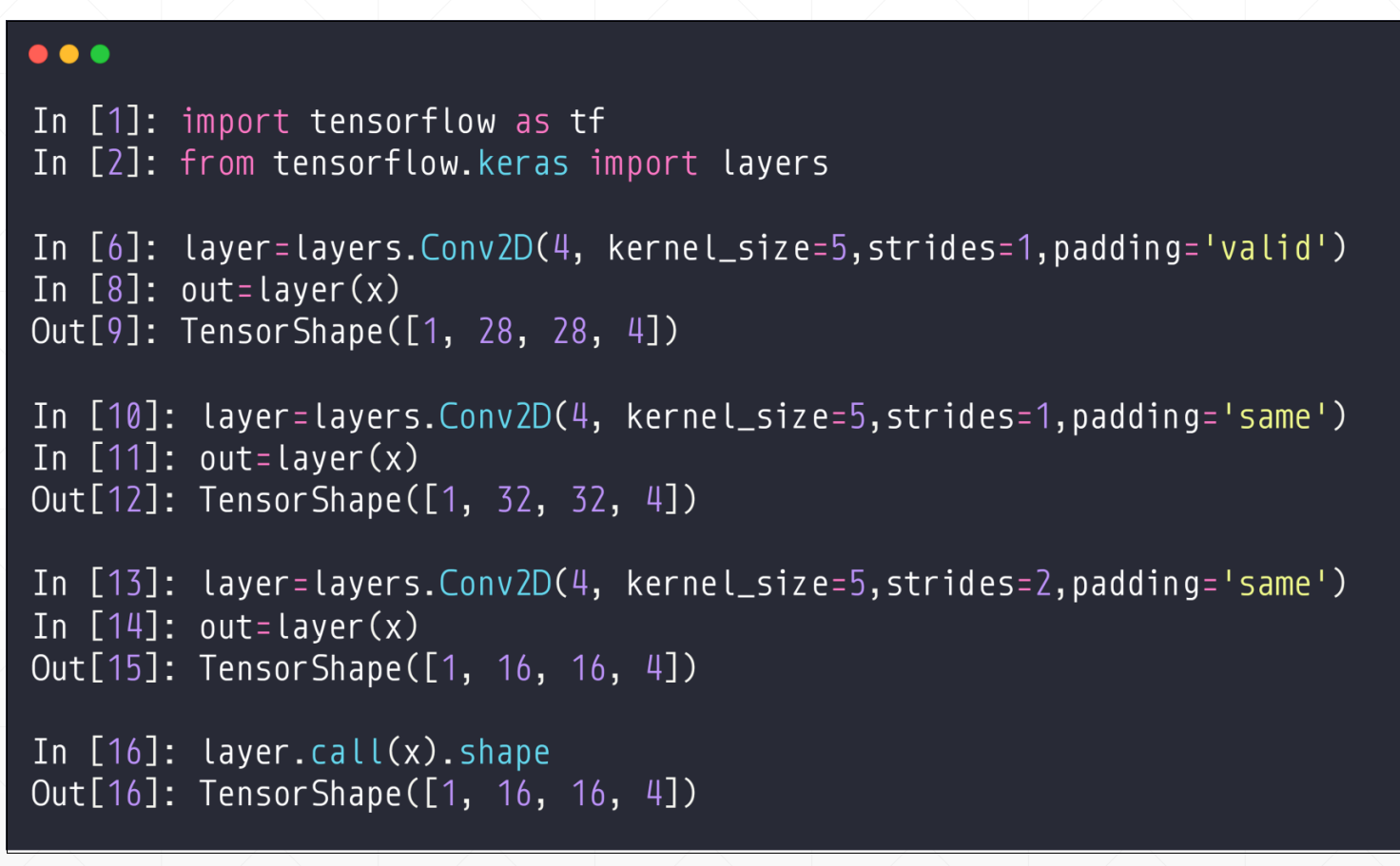
在这里我们我们之前说过直接调用layer(x)和调用layer.call(x)是一样的。
但是不建议用layer.call(x)
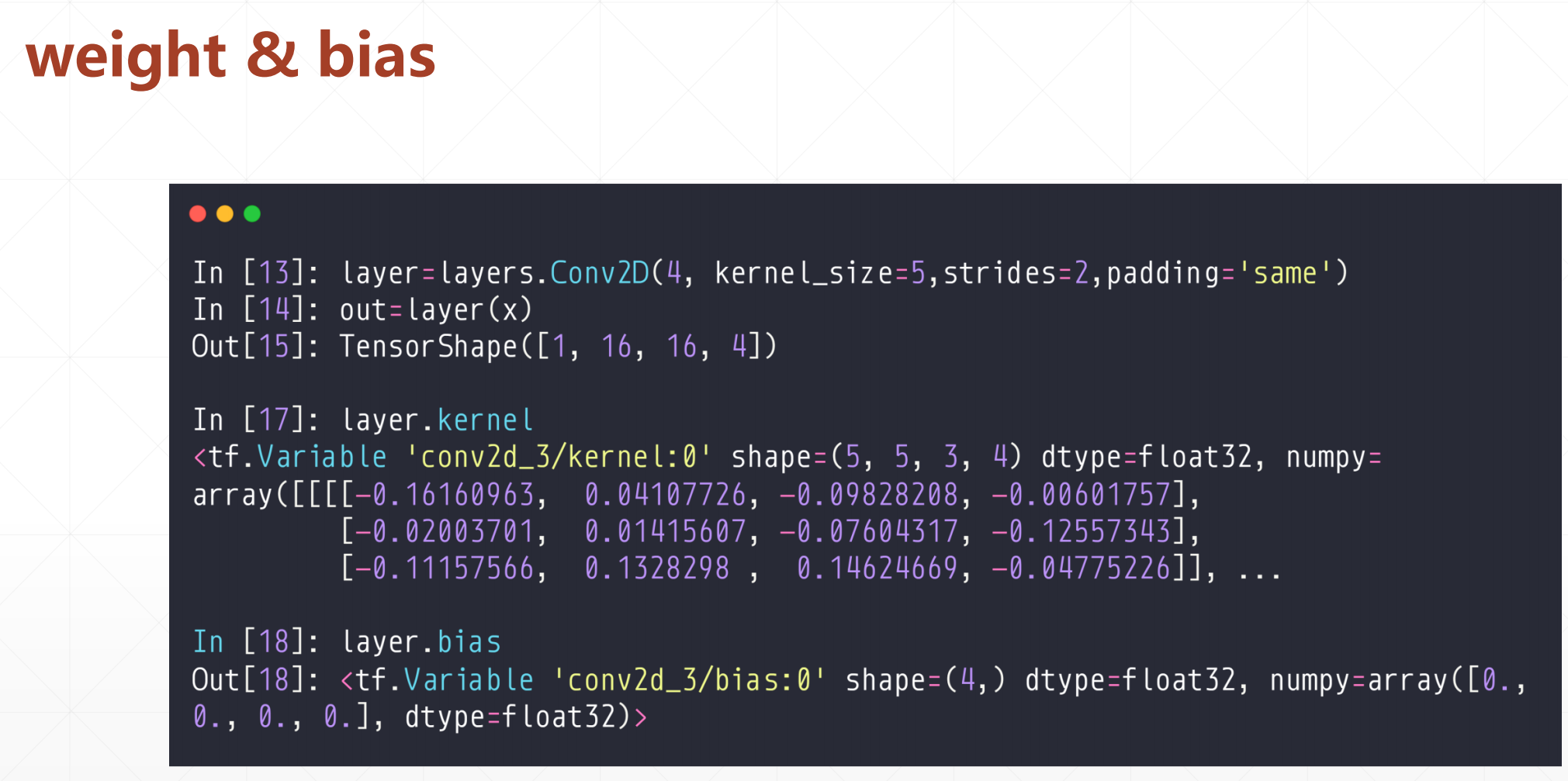
我们可以看到这个里面N,C,h,w的顺序。
7 Gradient
然后还有一个更为关键的事情就是Gradient
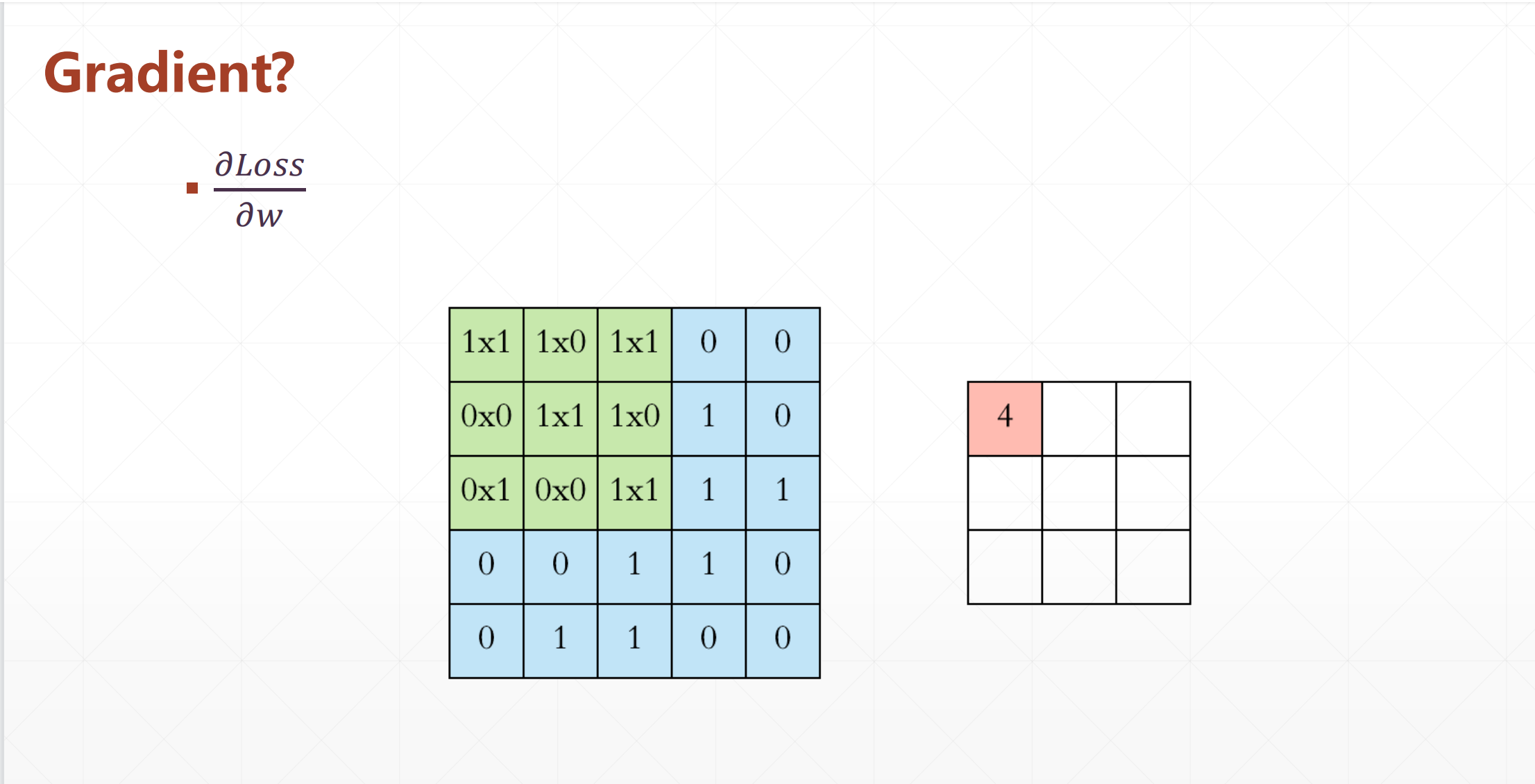
我们发现这个是很好求导的。
\(1*1\) 的卷积核
1*1的卷积核就是为了降维的，就是减少或者增加其通道数量
