2.5 特征工程之特征降维与主成分分析（PCA）

1.什么是特征降维

降低的对象为二维数组
此处的降维为降低特征的个数
降维是指在某些限定条件下，降低随机变量（特征）个数，得到一组“不相关”主变量的过程

降维的效果就是使得特征和特征之间不相关，来达到简化数据，简化工作量的目的
相关特征(correlated feature)

• 相对湿度与降雨量之间的相关
• 等等

如果相关的特征太多的话会造成数据的冗余的

正是因为在进行训练的时候，我们都是使用特征进行学习。如果特征本身存在问题或者特征之间相关性较强，对于算法学习预测会影响较大

2 降维的两种方式

降维的两种方式

特征选择
主成分分析（可以理解一种特征提取的方式）

2.1 特征选择

2.1.1 定义

数据中包含冗余或相关变量（或称特征、属性、指标等），旨在从原有特征中找出主要特征

2.1.2 方法

Filter(过滤式)：主要探究特征本身特点、特征与特征和目标值之间关联
方差选择法：低方差特征过滤(比如说是否有爪子这一个特征方差一定很小，过滤掉)
相关系数：特征与特征之间的相关程度(如果两个特征非常相关则可以去掉一个，需要计算相关系数)

Embedded(嵌入式)：算法自动选择特征（特征与目标值之间的关联）
决策树：信息熵、信息增益
正则化：L1、L2
深度学习：卷积等

2.1.3 API

sklearn.feature_selection

2.1.4 过滤式（方差选择法）

删除低方差的一些特征。再结合方差的大小来考虑这个方式的角度
特征方差小：某个特征大多样本的值比较相近
特征方差大：某个特征很多样本的值都有差别

过滤式API

（1）sklearn.feature_selection.VarianceThreshold(threshold = 0.0)
删除所有方差低于threshold的特征
（2）Variance.fit_transform(X)
--------X:numpy array 格式的数据[n_samples,n_features]
-------返回值：训练集差异低于 threshold 的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。

方法和前面的一样，也是
先实例化一个转化器类
再调用fit_transform

from sklearn.feature_selection import VarianceThreshold
def variance_demo():
    """
    过滤低方差特征
    :return:
    """
    # 1.获取数据
    data=pd.read_csv("factor_returns.csv")
    data=data.iloc[:,1:-2]
    print("data:\n",data)
    # 2.实例化一个转换器类
    transfer=VarianceThreshold(threshold=10)#具体调
    # 3.调用fit_transform
    data_new=transfer.fit_transform(data)
    print("data_new:\n",data_new,data_new.shape)
    return None

2.1.5 相关系数

皮尔逊相关系数(Pearson Correlation Coefficient)
反映变量之间相关关系密切程序的统计指标
如果两个系数相关性很强的话这可以去掉一个

公式

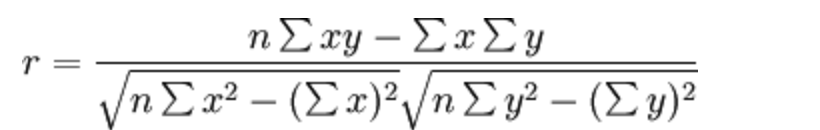
特点
相关系数的值介于-1 与+1 之间，即-1 <= r <= +1。其性质如下：
当 r>0 时，表示两变量正相关，r<0 时，两变量为负相关
当|r|=1 时，表示两变量为完全相关，当 r=0 时，表示两变量间无相关关系
当 0<|r|<1 时，表示两变量存在一定程序的相关。且|r|越接近 1，两变量间线性关系越密切；|r|越接近于 0，表示两变量的线性相关越弱
一般可按三级划分：|r|<0.4 为低度相关；0.4<=r<0.7 为显著性相关；0.7<=|r|<1 为高度线性相关
例如：

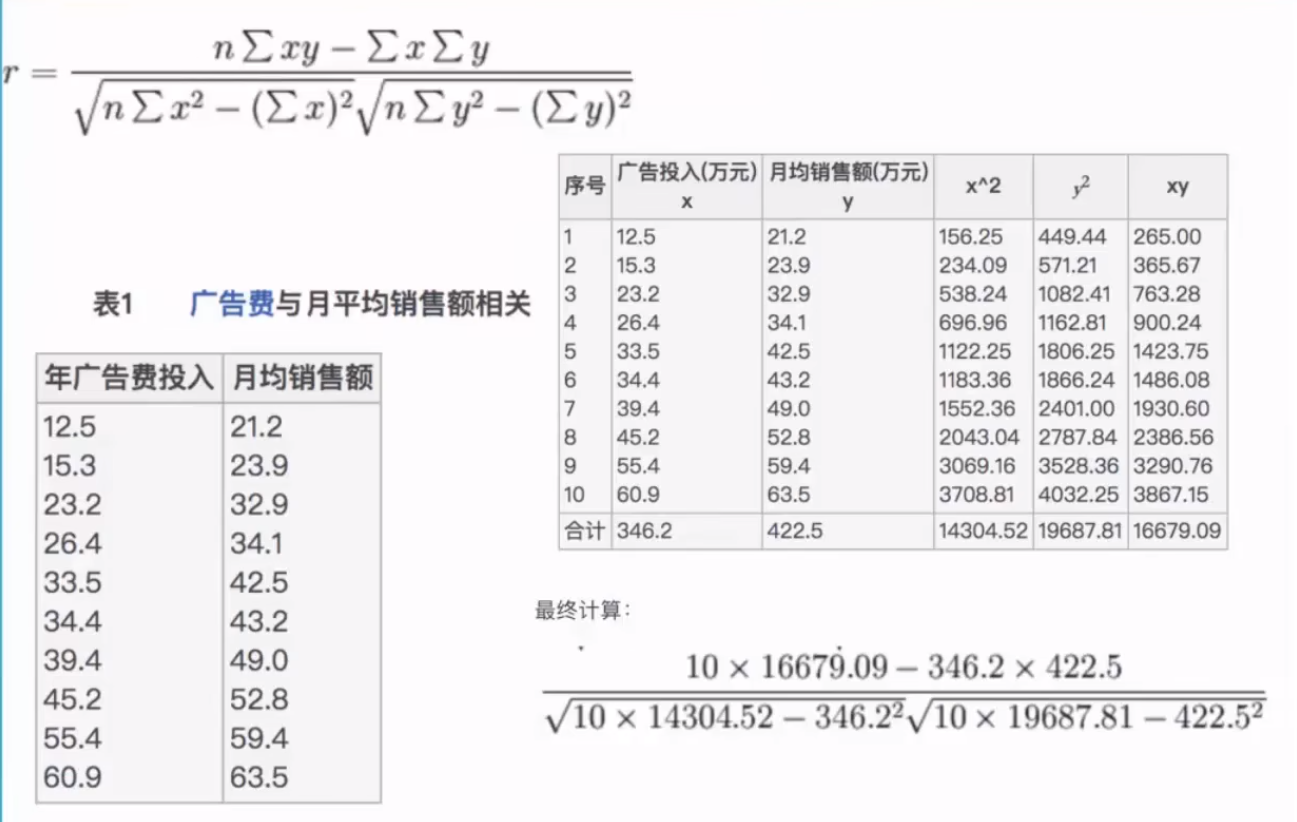
=0.9942
相关系数API

from scipy.stats import pearsonr
---x: (N,) array_like 
---y: (N,) array_like
Returns: (Pearson's correlation coefficient, p-value)

2.1.6 案例：股票的财务指标相关性计算

factor = ['pe_ratio','pb_ratio','market_cap','return_on_asset_net_profit','du_return_on_equity','ev','earnings_per_share','revenue','total_expense']

代码：算两个变量之间的相关系数

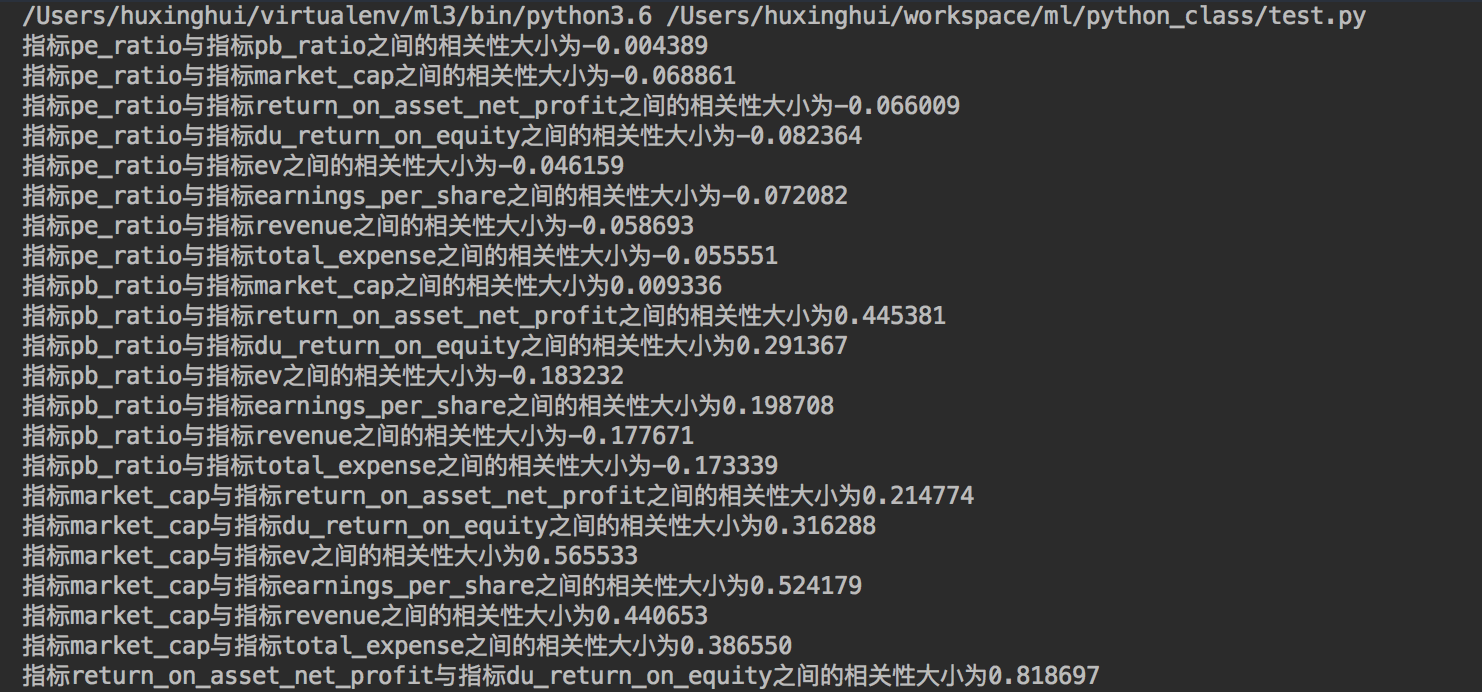
from scipy.stats import pearsonr

def variance_demo():
    """
    过滤低方差特征
    :return:
    """
    # 1.获取数据
    data=pd.read_csv("factor_returns.csv")
    data=data.iloc[:,1:-2]
    print("data:\n",data)
    # 2.实例化一个转换器类
    transfer=VarianceThreshold(threshold=10)
    # 3.调用fit_transform
    data_new=transfer.fit_transform(data)
    print("data_new:\n",data_new,data_new.shape)

    #计算某两个变量之间的相关系数
    r=pearsonr(data["pe_ratio"],data["pb_ratio"])
    print("相关系数：\n",r)
    return None

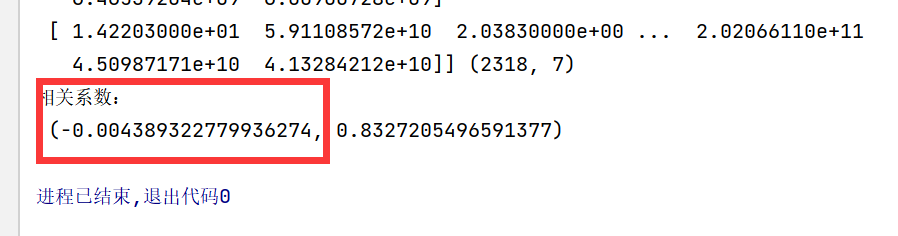
从中我们得出
指标revenue与指标total_expense之间的相关性大小为0.995845
指标return_on_asset_net_profit与指标du_return_on_equity之间的相关性大小为0.818697

我们也可以通过画图来观察结果

import matplotlib.pyplot as plt
plt.figure(figsize=(20, 8), dpi=100)
plt.scatter(data['revenue'], data['total_expense'])
plt.show()

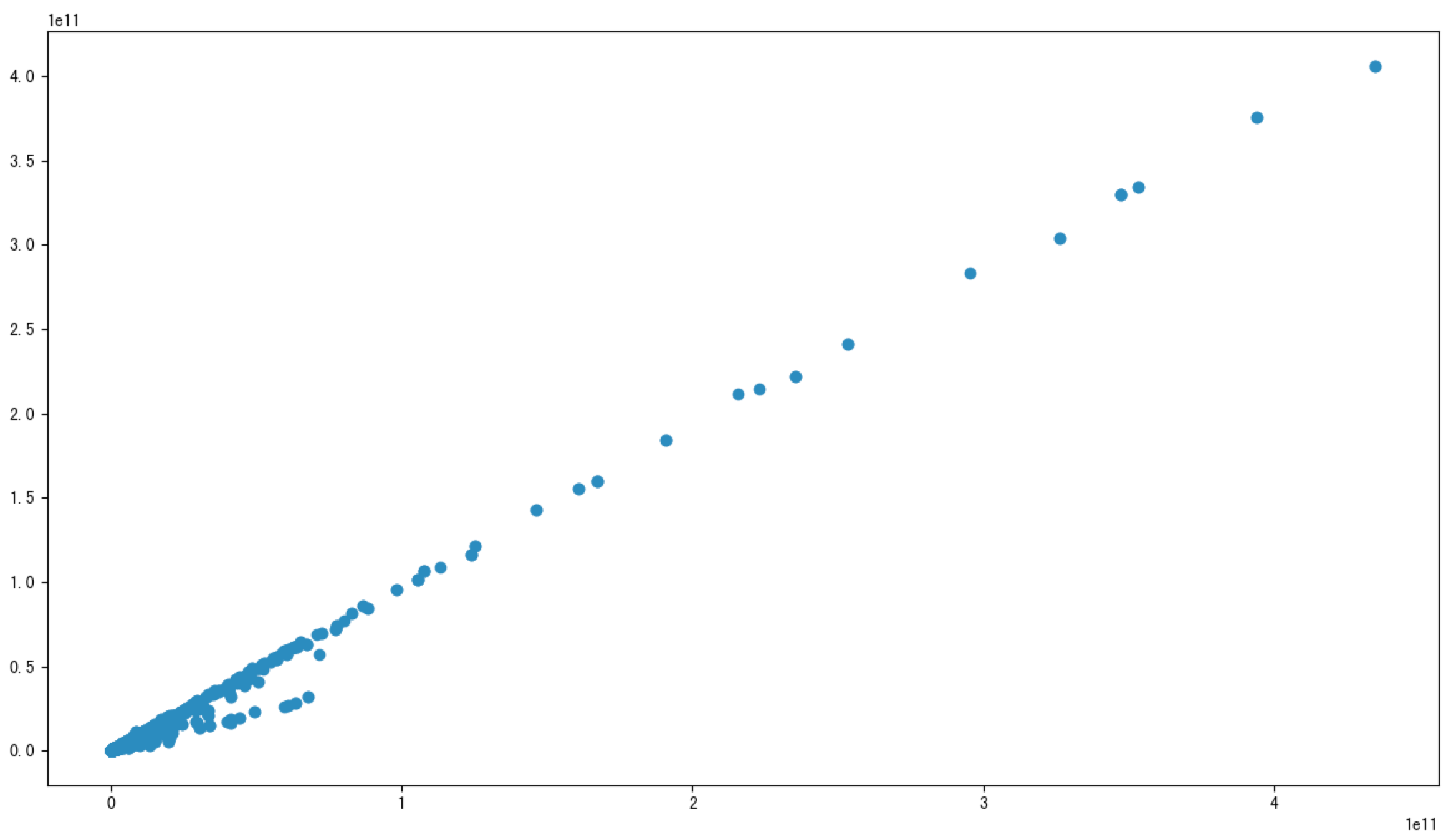
这两对指标之间的相关性较大，可以做之后的处理，比如合成这两个指标。

如果两个特征之间的相关系性很高我们应该怎么选择呢
（1）选其中一个
（2）加权求和
（3）主成分分析

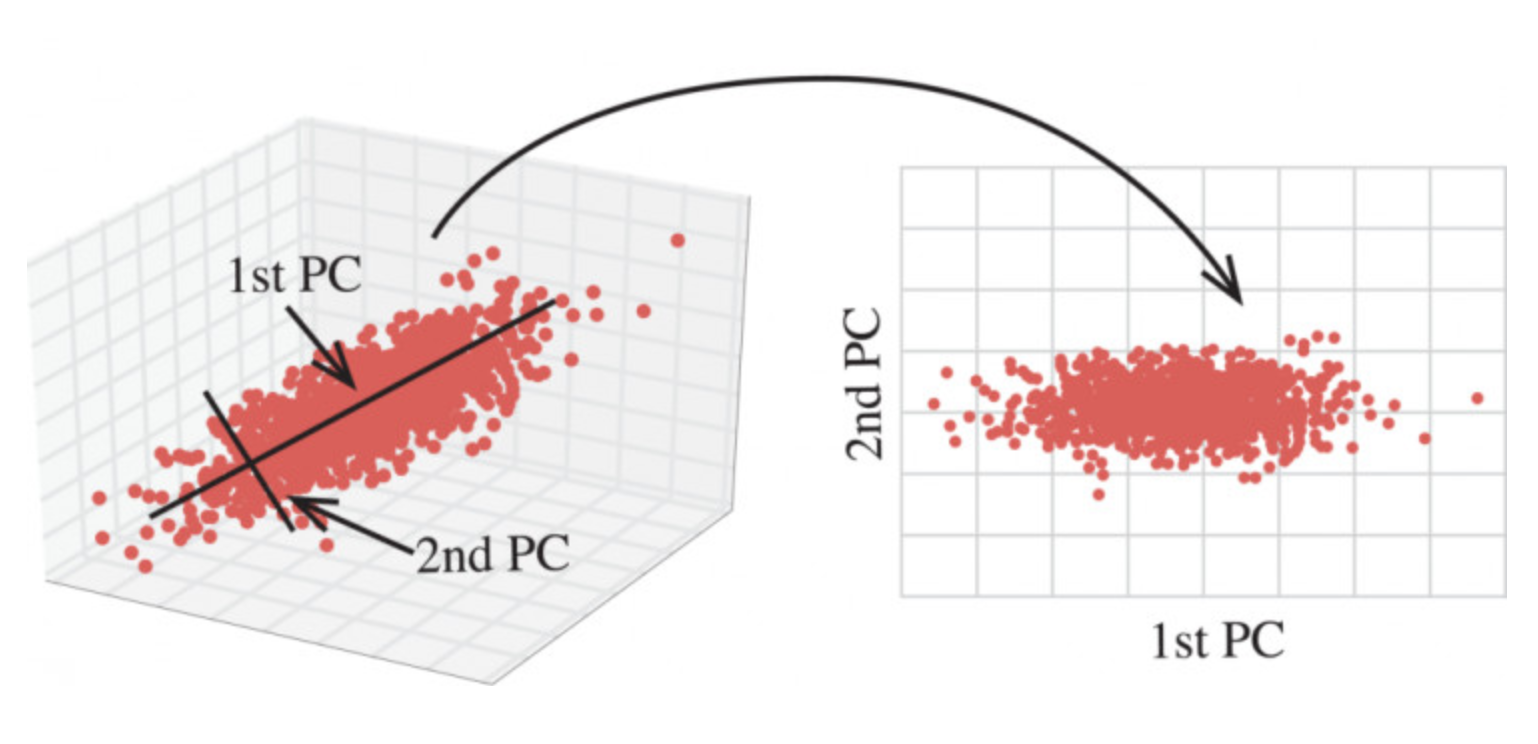
2.2 主成分分析（PCA）

定义：高维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量**
作用：是数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。
应用：回归分析或者聚类分析**

就是将三维的降到二维，它会有一些损失（信息损失了多少），其实一个很直观的反应就是看看我们通过这个二维的图像还能不能看出来这是个水壶

例如这个最后一个降维之后损失的最少，我们还能看出来他是个水壶

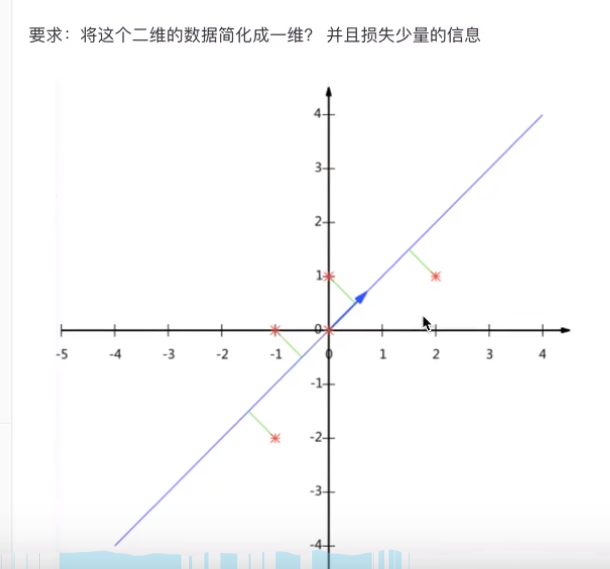
再例如将这个二维的降到一维（直线）

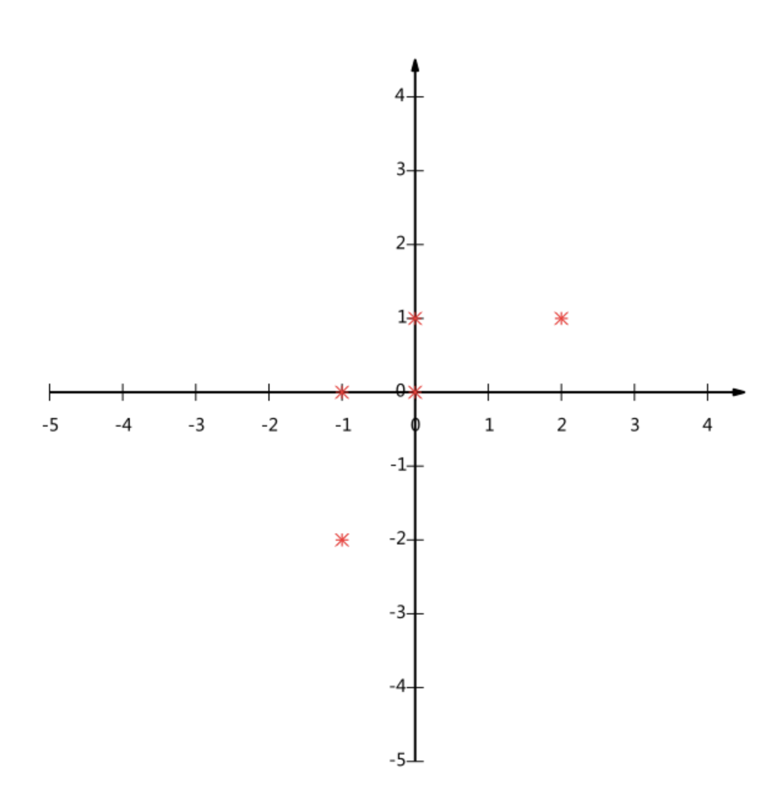
这样做是损失的最少


API

sklearn.decomposition.PCA(n_components=None)
  将数据分解为较低维数空间
  n_components:
   小数：表示保留百分之多少的信息
   整数：减少到多少特征(比如是个2，就是降到二维)
  PCA.fit_transform(X) X:numpy array 格式的数据[n_samples,n_features]
返回值：转换后指定维度的 array

步骤
1、实例化一个转换器类
2、调用fit_transform

代码
先拿个简单的数据计算一下

[[2,8,4,5],
[6,3,0,8],
[5,4,9,1]]

from sklearn.decomposition import PCA
def pca_demo():
    """
    PCA降维
    :return:
    """
    data = [[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]]

    # 1、实例化一个转换器类
    # transfer = PCA(n_components=2)#指定降到2维
    transfer = PCA(n_components=0.95)#保留95%的信息

    # 2、调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n", data_new)

    return None

保留90%的信息，降维结果为：
 [[ -3.13587302e-16   3.82970843e+00]
 [ -5.74456265e+00  -1.91485422e+00]
 [  5.74456265e+00  -1.91485422e+00]]
降维到3维的结果：
 [[ -3.13587302e-16   3.82970843e+00   4.59544715e-16]
 [ -5.74456265e+00  -1.91485422e+00   4.59544715e-16]
 [  5.74456265e+00  -1.91485422e+00   4.59544715e-16]]

具体案例

用户和类别之间的关系

1 需求


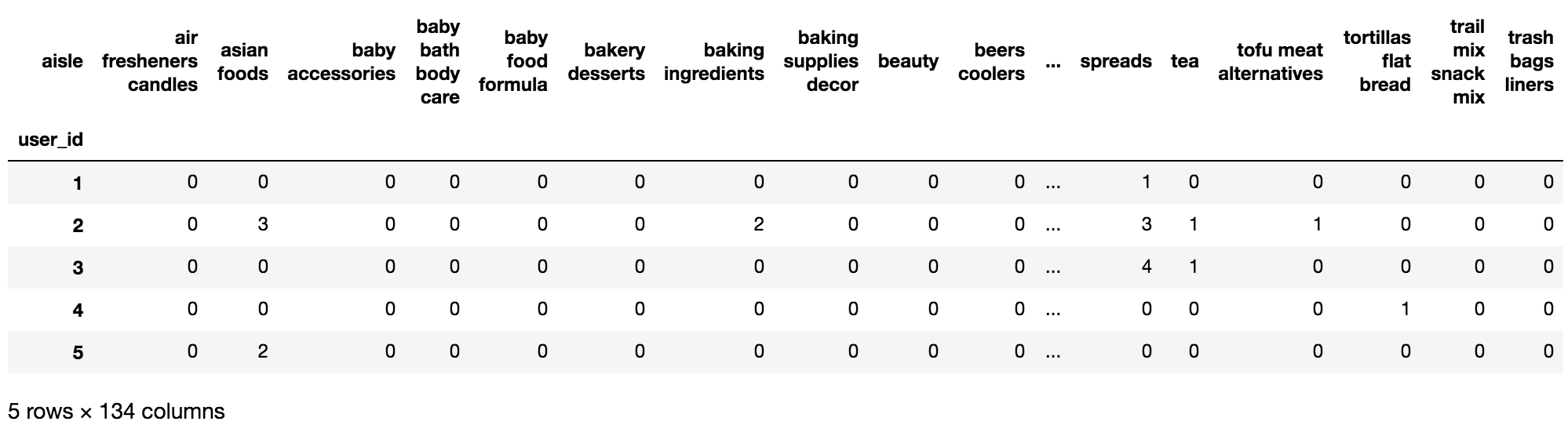
分析
合并表，使得user_id与aisle在一张表当中
进行交叉表变换
进行降维

import pandas as pd
from sklearn.decomposition import PCA

# 1、获取数据集
# ·商品信息- products.csv：
# Fields：product_id, product_name, aisle_id, department_id
# ·订单与商品信息- order_products__prior.csv：
# Fields：order_id, product_id, add_to_cart_order, reordered 
# ·用户的订单信息- orders.csv：
# Fields：order_id, user_id,eval_set, order_number,order_dow, order_hour_of_day, days_since_prior_order 
# ·商品所属具体物品类别- aisles.csv：
# Fields：aisle_id, aisle     
products = pd.read_csv("./instacart/products.csv")
order_products = pd.read_csv("./instacart/order_products__prior.csv")
orders = pd.read_csv("./instacart/orders.csv")
aisles = pd.read_csv("./instacart/aisles.csv")

# 2、合并表，将user_id和aisle放在一张表上
# 1）合并orders和order_products on=order_id tab1:order_id, product_id, user_id
tab1 = pd.merge(orders, order_products, on=["order_id", "order_id"])
# 2）合并tab1和products on=product_id tab2:aisle_id
tab2 = pd.merge(tab1, products, on=["product_id", "product_id"])
# 3）合并tab2和aisles on=aisle_id tab3:user_id, aisle
tab3 = pd.merge(tab2, aisles, on=["aisle_id", "aisle_id"])

# 3、交叉表处理，把user_id和aisle进行分组
table = pd.crosstab(tab3["user_id"], tab3["aisle"])

# 4、主成分分析的方法进行降维
# 1）实例化一个转换器类PCA
transfer = PCA(n_components=0.95)
# 2）fit_transform
data = transfer.fit_transform(table)

data.shape

返回结果：

(206209, 44)