矩阵中最大的三个菱形和(斜向前缀和)
给你一个 m x n 的整数矩阵 grid 。
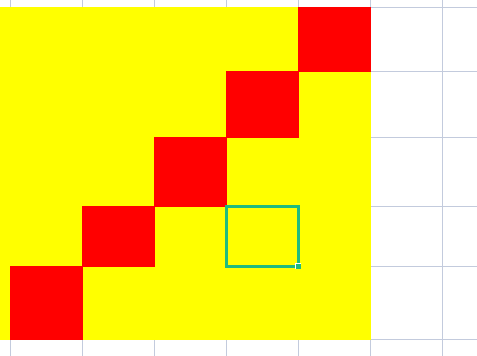
菱形和 指的是 grid 中一个正菱形边界上的元素之和。本题中的菱形必须为正方形旋转45度,且四个角都在一个格子当中。下图是四个可行的菱形,每个菱形和应该包含的格子都用了相应颜色标注在图中。
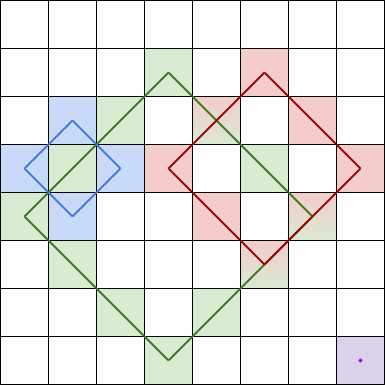
注意,菱形可以是一个面积为 0 的区域,如上图中右下角的紫色菱形所示。
请你按照 降序 返回 grid 中三个最大的 互不相同的菱形和 。如果不同的和少于三个,则将它们全部返回。
示例 1:
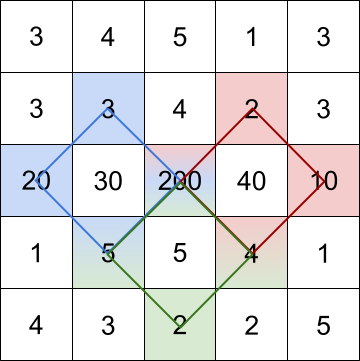
输入:grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]
输出:[228,216,211]
解释:最大的三个菱形和如上图所示。
- 蓝色:20 + 3 + 200 + 5 = 228
- 红色:200 + 2 + 10 + 4 = 216
- 绿色:5 + 200 + 4 + 2 = 211
示例 2:
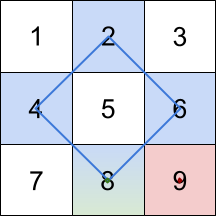
输入:grid = [[1,2,3],[4,5,6],[7,8,9]]
输出:[20,9,8]
解释:最大的三个菱形和如上图所示。
- 蓝色:4 + 2 + 6 + 8 = 20
- 红色:9 (右下角红色的面积为 0 的菱形)
- 绿色:8 (下方中央面积为 0 的菱形)
示例 3:
输入:grid = [[7,7,7]]
输出:[7]
解释:所有三个可能的菱形和都相同,所以返回 [7] 。
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 100
1 <= grid[i][j] <= 1e5
这个题的意思就是说的给你一个矩阵,然后在矩阵中找一些(旋转了45度的正方形)。然后这个矩形的权值就是他的四个边经过的矩形的值(我们会发现经过的都是
矩阵的中心)
我们发现先这个n和m的数据范围是100所以我们可以三层for循环来做的,就是两层for枚举出来它的中心点,然后一层for枚举它的边长
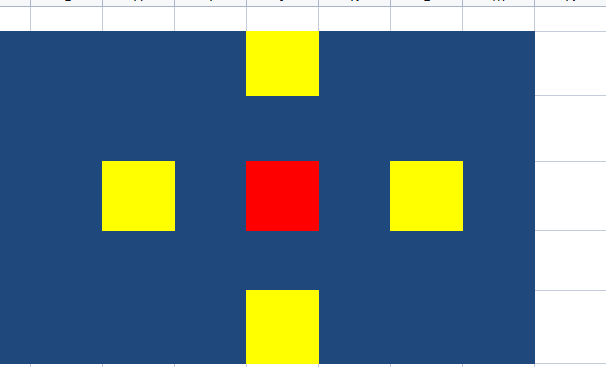
然后还有一个问题就是怎么计算这个四个边的和呢,如果暴力算的话一定会超时的
这里我们有一个类似与前缀和的算法就是斜向前缀和,这斜向前缀和有两个方向一个是从左上到右下,一个是从右上到左下
我们令s1为从左上到右下

就是这样,我们求s1数组的时候就是,然后就是这个红线的和为s1[x2][y2]-s1[x1-1][y1-1]
for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ s1[i][j]=s1[i-1][j-1]+g[i-1][j-1]; s2[i][j]=s2[i-1][j+1]+g[i-1][j-1]; } }
然后这个反方向就是
就是这样
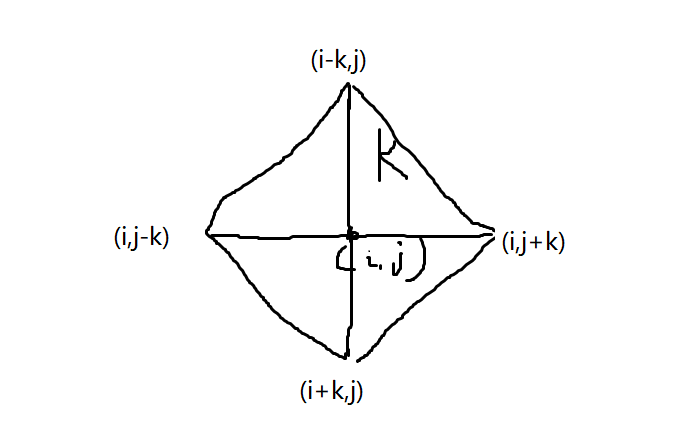
代码中需要注意一下这个有的点没加上
const int maxn=110; int s1[maxn][maxn],s2[maxn][maxn]; class Solution { public: vector<int> getBiggestThree(vector<vector<int>>& g) { int n=g.size(),m=g[0].size(); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ s1[i][j]=s1[i-1][j-1]+g[i-1][j-1]; s2[i][j]=s2[i-1][j+1]+g[i-1][j-1]; } } set<int> S; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){//枚举中间点 S.insert(g[i-1][j-1]); for(int k=1;i-k>=1&&i+k<=n&&j-k>=1&&j+k<=m;k++){//枚举边长 int a=s2[i][j-k]-s2[i-k][j]; int b=s1[i][j+k]-s1[i-k][j]; int c=s2[i+k][j]-s2[i][j+k]; int d=s1[i+k][j]-s1[i][j-k]; S.insert(a+b+c+d-g[i+k-1][j-1]+g[i-k-1][j-1]); } } while(S.size()>3){ S.erase(S.begin()); } } return vector<int>(S.rbegin(),S.rend()); } };


