C. Parsa's Humongous Tree(树形dp)

传送门

帕尔萨的巨树

帕尔萨有一棵巨大的树，上面有n个顶点。

在每个顶点v上，他写了两个整数lv和rv

为了让Parsa的树看起来更宏伟，Nima想给每个顶点v分配一个数字avav (lv≤av≤rv)，这样Parsa的树的美丽就被最大化了。

尼玛的美感是相当奇怪的。他把树的美定义为|au−av|对树的所有边(u,v)的和。

由于帕尔萨的树太大了，尼玛无法凭借自己的力量将它的美丽最大化。你的任务是找出帕尔萨树的最大美感。

输入
第一行包含一个整数tt(1≤t≤250)-测试用例的数量。测试用例的描述如下。

每个测试用例的第一行包含一个整数nn(2≤n≤1e5) - Parsa树的顶点数。

下面的第i个nn行包含两个整数li和ri(1≤li≤ri≤1e9)。

接下来的n - 1行每一行包含两个整数u和v(1≤u,v≤n,u≠v)，这意味着在帕尔萨树的uu和v之间有一条边。

可以保证给定的图是树。

该方法保证所有测试用例的nn之和不超过2⋅1e5。

输出
对于每个测试用例，打印出Parsa树的最大可能美感。

例子
输入
复制
3.
2
１ ６
3 8
1 2
3.
1 3
4 - 6
7 9
1 2
2 3
6
3 14
12个20
12日19
2 12
10日17
3 17
3 - 2
6 5
1 - 5
2 - 6
4 - 6
输出
复制
7
8
62

请注意
例子中的树:

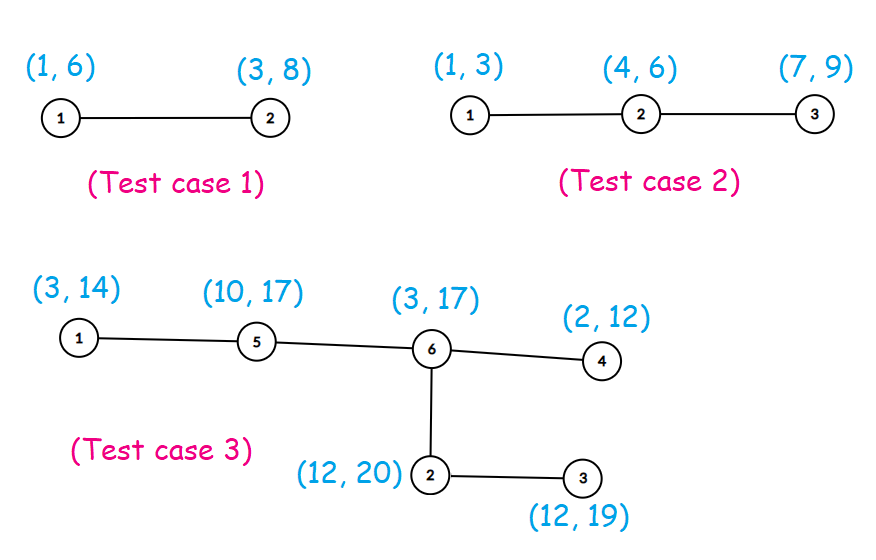
In the first test case, one possible assignment is a={1,8} which results in |1−8|=7

In the second test case, one of the possible assignments is a={1,5,9} which results in a beauty of |1−5|+|5−9|=8

 

这个题就是一个树形dp

首先树上每一个节点都是选这li或者是ri的，这个是可以证明的

dp[i][0]为第i个点选择最小值，并且以ｉ为根节点的最大值
dp[i][1]为第i个点选择最大值，并且以ｉ为根节点的最大值

所以这个最后的结果就是ｍａｘ（ｄｐ［１］［１］，ｄｐ［１］［０］）

就是这样

 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
typedef long long ll; 
const int maxn=6e5+100;
vector<int>e[maxn];
struct node{
    ll l,r;
}a[maxn];
ll dp[maxn][2];//dp[i][0]代表的是以i为根节点选最大值
//dp[i][1]代表的是节点选的是最小值
void dfs(int u,int fa){
    for(int i=0;i<e[u].size();i++){
        int v=e[u][i];
        if(v==fa){
            continue;
        }
        dfs(v,u);
        dp[u][0]+=max(dp[v][0]+abs(a[v].r-a[u].r),dp[v][1]+abs(a[v].l-a[u].r));
        dp[u][1]+=max(dp[v][0]+abs(a[v].r-a[u].l),dp[v][1]+abs(a[v].l-a[u].l));
    }
} 
int main(){
    int t;
    cin>>t;
    while(t--){
        memset(dp,0,sizeof(dp));
        int n;
        cin>>n;
        for(int i=1;i<=n;i++){
            e[i].clear();
            scanf("%lld%lld",&a[i].l,&a[i].r);
        }
        for(int i=1;i<=n-1;i++){
            int x,y;
            scanf("%d%d",&x,&y);
            e[x].push_back(y);
            e[y].push_back(x); 
        }
        dfs(1,-1);
        cout<<max(dp[1][0],dp[1][1])<<endl;
    }
}


/*

*/