月月给华华出题

 链接：https://ac.nowcoder.com/acm/contest/392/D
来源：牛客网

 

输入描述:

一个正整数n。

输出描述:

输出n行，第i行表示N=i时的答案。

示例1

输入

6

输出

1
2
4
6
11
11

备注:

1≤n≤1e6
请注意输出的效率

思路：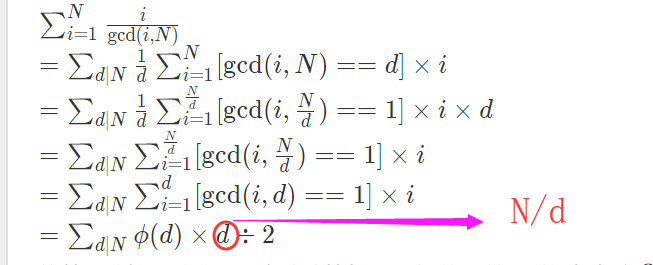

最后一步是根据这个欧拉函数的一个得出的：

小于等于n的数中与n互质的数sum和为phi(n) * n/2

phi（x）为欧拉函数

由于题目要求输出1~n的每一个答案，那么我们从1到n枚举i当做上式中因子d来计算对每个答案的贡献即可。

 

 

#include <iostream>
#include<algorithm>
using namespace std; 
typedef long long ll;
const int maxn=3e6+100;
int ol[maxn];
int prime[maxn];
int cnt;
ll f[maxn];
int n;
void inint(){
    ol[1]=1;
    for(int i=2;i<maxn;i++){
        if(!ol[i]){
            prime[++cnt]=i;
            ol[i]=i-1;
        }
        for(int j=1;j<=cnt&&i*prime[j]<maxn;j++){
            if(i%prime[j]==0){
                ol[i*prime[j]]=ol[i]*prime[j];
                break;
            } 
            else{
                ol[i*prime[j]]=ol[i]*(prime[j]-1);
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=i;j<=n;j+=i){
            f[j]+=1ll*ol[i]*i/2;
        }
    }
}
int main(){
    cin>>n;
    inint();
    for(int i=1;i<=n;i++){
        printf("%lld\n",f[i]+1);
    }
}