【K倍区间-蓝桥杯原题/取模+前缀和】

从左到右一排有N个盒子。左边第一个盒子里装的是糖果。

你将把糖果从一些连续的盒子里拿出来，均匀地分发给M个孩子。

在这种情况下，找出满足下列条件的对(l,r)的数目:

l和r都是整数，满足1≤l≤r≤N.Al+Al+1+…+Ar是M的倍数。

约束

·输入的所有值都是整数。

·1≤N≤105

·2≤≤109

Ai·1≤≤109

输入

输入来自标准输入，格式如下:

 

N M

A1 A2……一个

 

输出

打印满足条件的对(l,r)的数目。

注意，该数字可能不适合32位整数类型。

 

样例输入副本

3 - 2

4 1 5

样例输出副本

3.

提示

 

·(1,1)的和:4

·(1,2)的和:5

·(1,3)的和:10

·(2,2)的和:1

·(2,3)的和:6

·(3,3)的和:5

其中3个是2的倍数。

前缀和+组合数学

 

由：（Sum[ R ]- Sum[ L-1 ]）%K==0;——》Sum[ R ]%K -Sum [ L - 1 ] %K==0

 

把该数列的每一项的前缀和%m,如果在序列中有n个前缀和(%m后的)都等于p(p!=0)则说明在这p段中选出两端就行，为。

特别注意当p==0，为+p.//p可以自成一段

首先我们知道表达一个区域『L，R』一定是用前缀和来处理对吧。

这个前缀和：sum[ R ]-sum[ L-1 ]。

我们想求一下K的倍数对吧。不就是对这个区域取模。

（Sum[ R ]- Sum[ L-1 ]）%K==0;

但是我们知道，Sum[ R ]%K -Sum [ L - 1 ] %K==0 这个式子是等价对吧。

那么我们找的就是 （Sum[ L ]%K==0）或者（Sum[ R ] - Sum [ L-1 ]）%K==0.

 

我们在任意一个   Sum【D】任意取两个作为两个端点就是，组合数：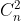

#include<iostream>
#include<algorithm>
#include<map>
#include <math.h> 
#include<memory.h>
using namespace std; 
typedef long long ll; 
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int maxn=5e5+100;
int a[maxn];
int sum[maxn];
map<int,int>mp;
int n,m; 
void inint(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        sum[i]=(sum[i-1]+a[i])%m;
        mp[sum[i]]++;
    }
}
int main(){
    inint();
    ll sum=mp[0];
    for(auto i=mp.begin();i!=mp.end();i++){
        ll s=i->second;
        sum+=(s*(s-1))/2;
    }
    printf("%lld",sum);    
}