深度强化学习基础（王树森）
王树森—深度强化学习基础
1 基本概念
概率论
随机变量：值取决于随机事件的结果
大写字母\(X\)表示随机变量，小写字母\(x\)表示随机变量的观测值
概率密度函数（Probability Density Function, PDF）：随机变量在某个确定的取值点附近的可能性
连续 or 离散
期望：
\(p(x)\)为概率密度函数
术语
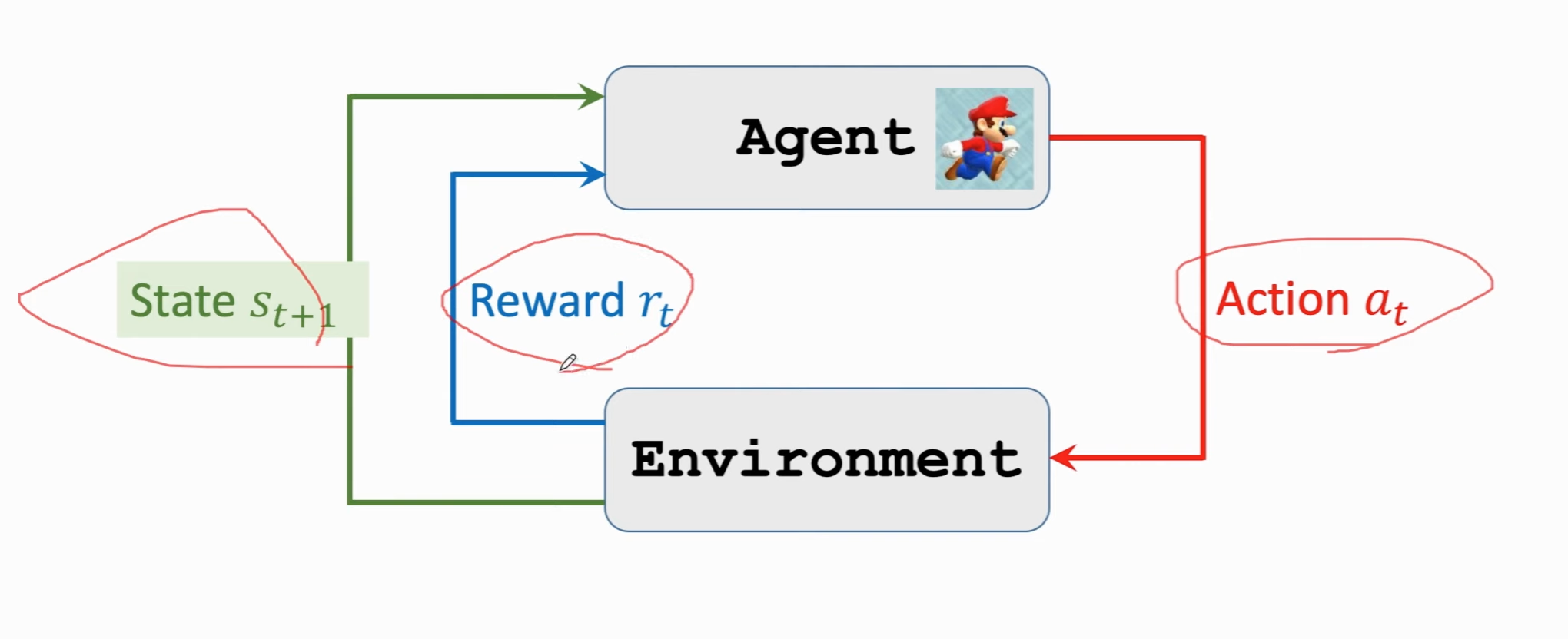
状态（state）
动作（action）
智能体（agent）：动作的执行者
策略（policy, \(\pi\)）：根据观测到的状态作出决策，控制智能体的运动
\(\pi:(s,a)\rarr [0,1]\)
\(\pi(a|s)=\mathbb{P}(A=a|S=s)\)
为什么要随机？博弈场景，确定的动作会让别人赢，因此policy最好是概率密度函数，action是随机抽样得到的
奖励（reward）：需要自己定义，对结果影响大。强化学习目标：获得奖励总和尽可能高。
状态转移（state transition）：当前状态下做一个动作，会转移到新的状态。可以是确定的，也可以是随机的（随机性从环境中来）。
状态转移函数：\(p(s'|s,a)=\mathbb{P}(S'=s'|S=s,A=a)\)
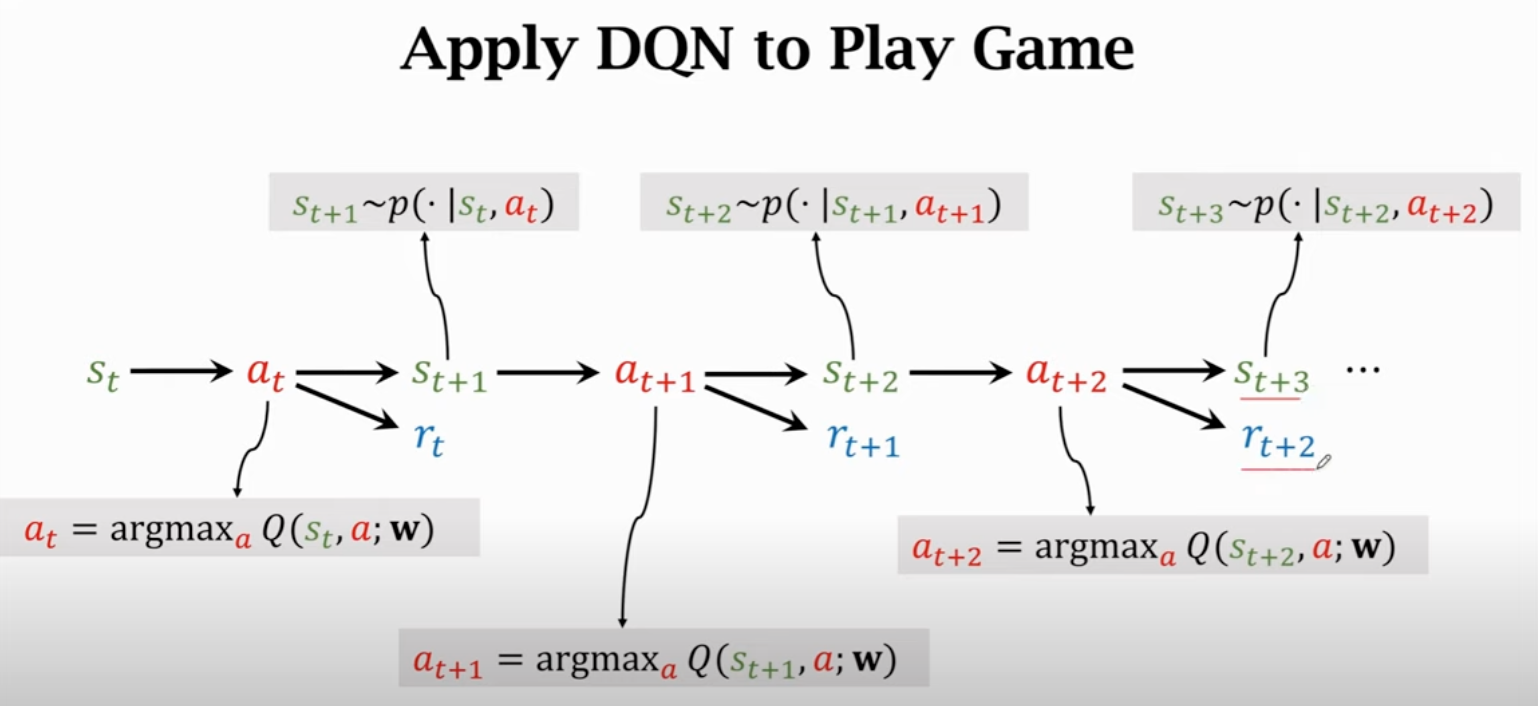
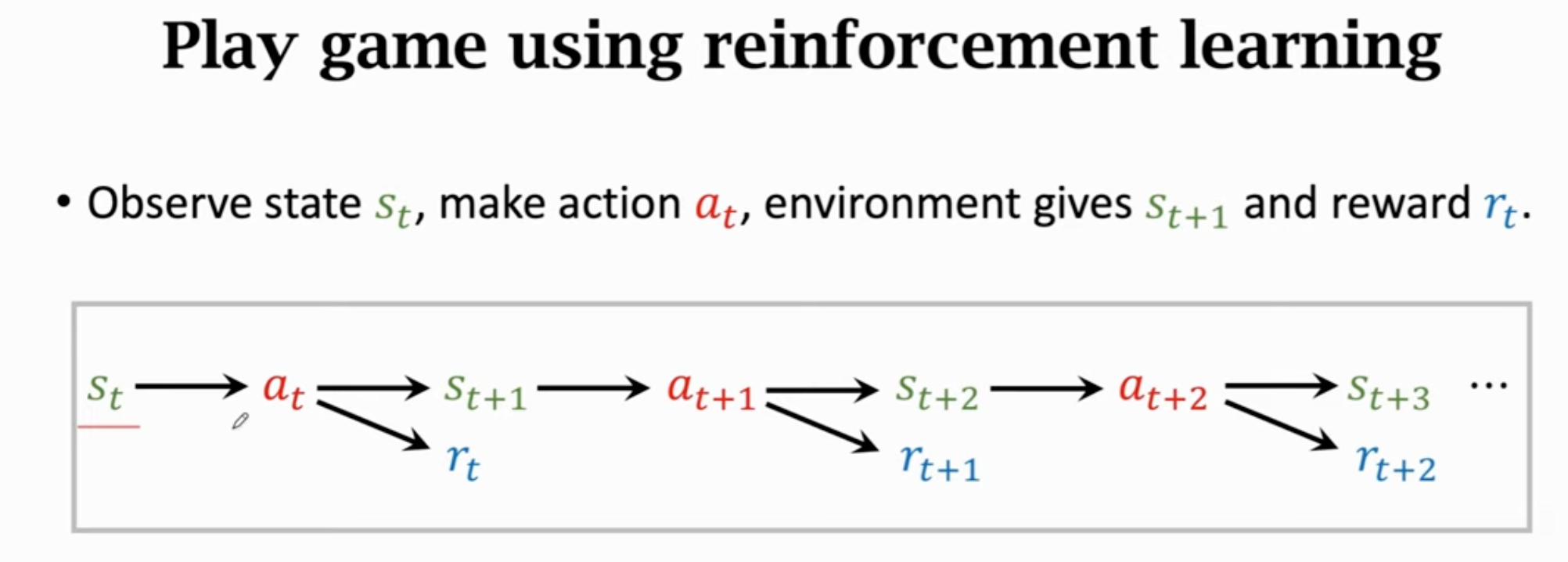
agent与环境交互：
强化学习中的随机性：
通过强化学习玩游戏：
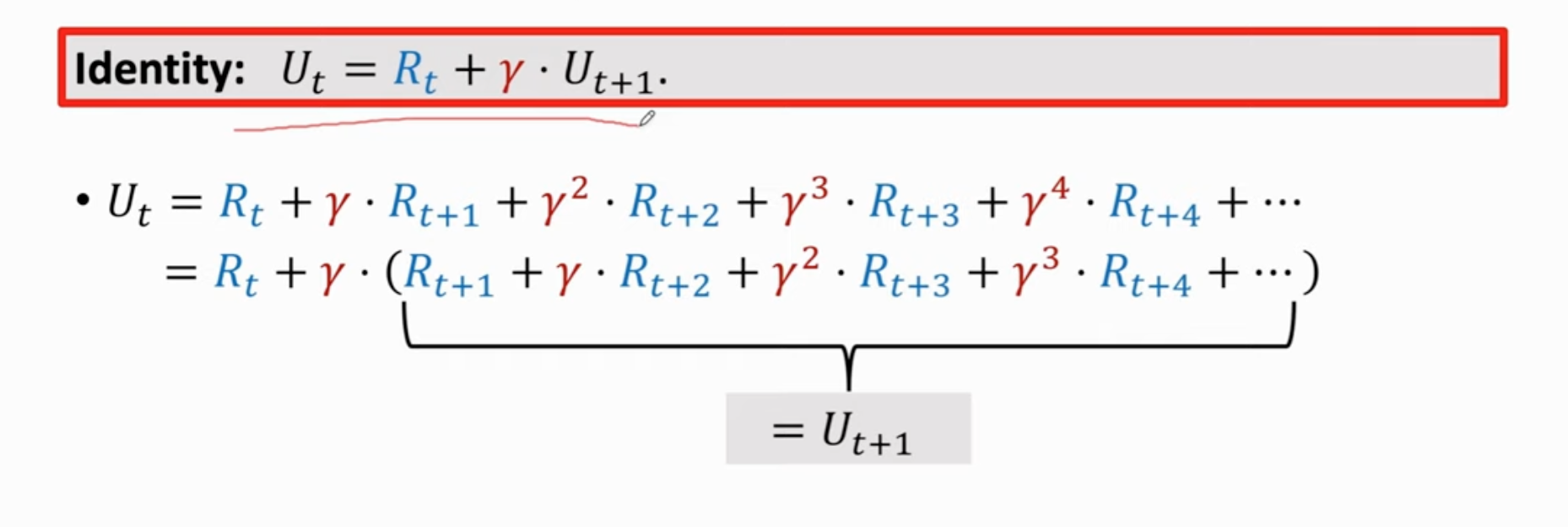
回报（return）：未来的累计奖励
\(U_t=R_t+R_{t+1}+...\)
\(R_t\)和\(R_{t+1}\)同样重要吗？不
折扣回报（discounted return）：\(\gamma\)为折扣率（可调节的超参数）。
\(U_t=R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+...\)
回报的随机性：假设游戏结束，奖励都观测到了，为具体的数值，则用小写字母表示；如果t时刻游戏还没有结束，奖励还没被观测到，就用大写字母\(R\)表示，折扣回报用大写字母\(U\)表示。
\(U_t\)依赖于：
动作价值函数 \(Q(s,a)\)：
\(Q_{\pi}(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]\)，除了\(S_t\)和\(A_t\)（观测到），未来其它的动作和状态都被积掉了；此外还依赖policy函数，可以知道对于这个policy函数，当前哪个动作好/不好
最优动作价值函数：可以对动作进行评价。
状态价值函数：判断当前状态好不好
如何用ai控制智能体？
summary
2 基于价值的强化学习
回顾：
\(Q^*\)可以指导agent做决策，不受策略函数的影响。
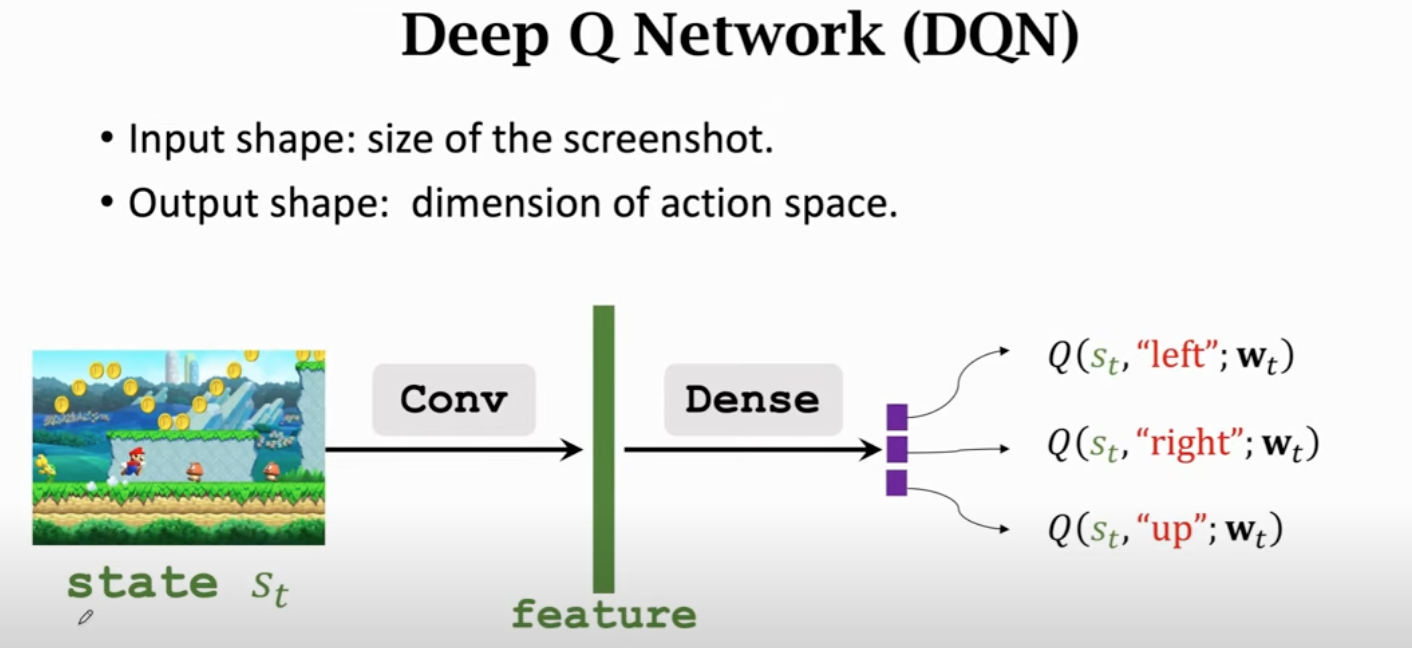
Deep Q-Network (DQN)
利用神经网络近似\(Q^{*}\)函数。
\(\textbf{w}\)为神经网络参数。
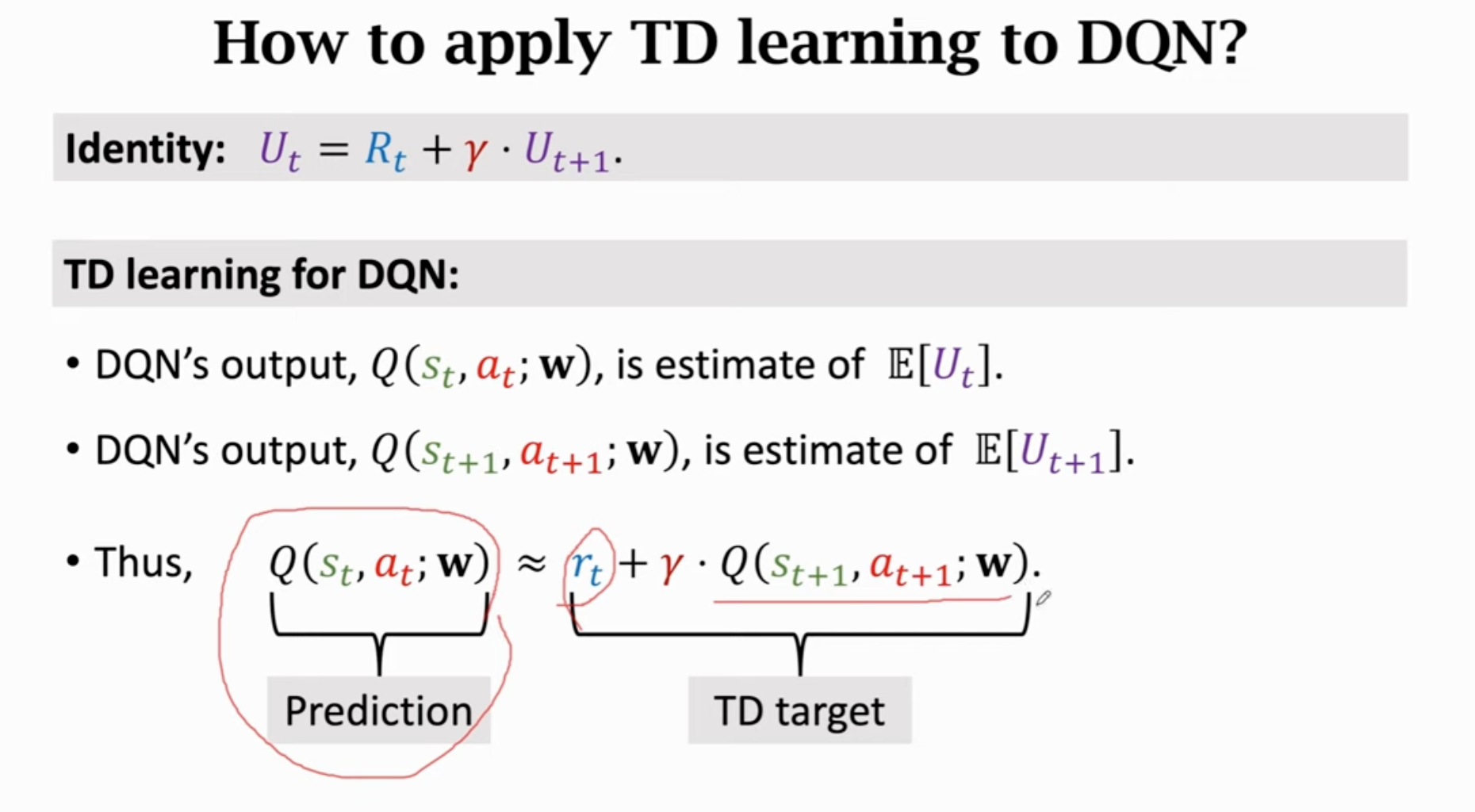
如何训练DQN：Temporal Difference（TD）算法
不需要经历整个过程（玩完整个游戏）就能更新模型参数
过程：
3 基于策略的强化学习
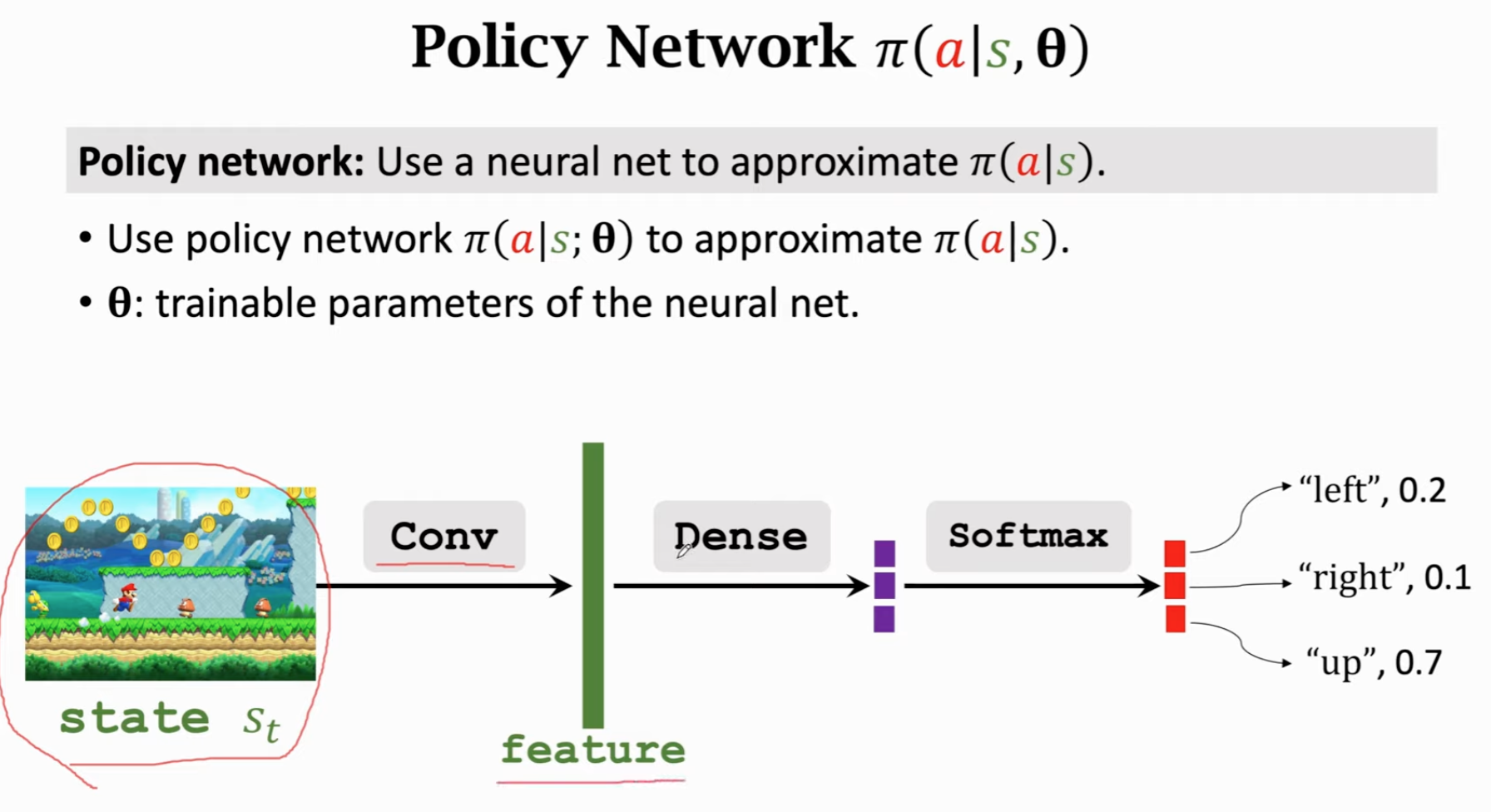
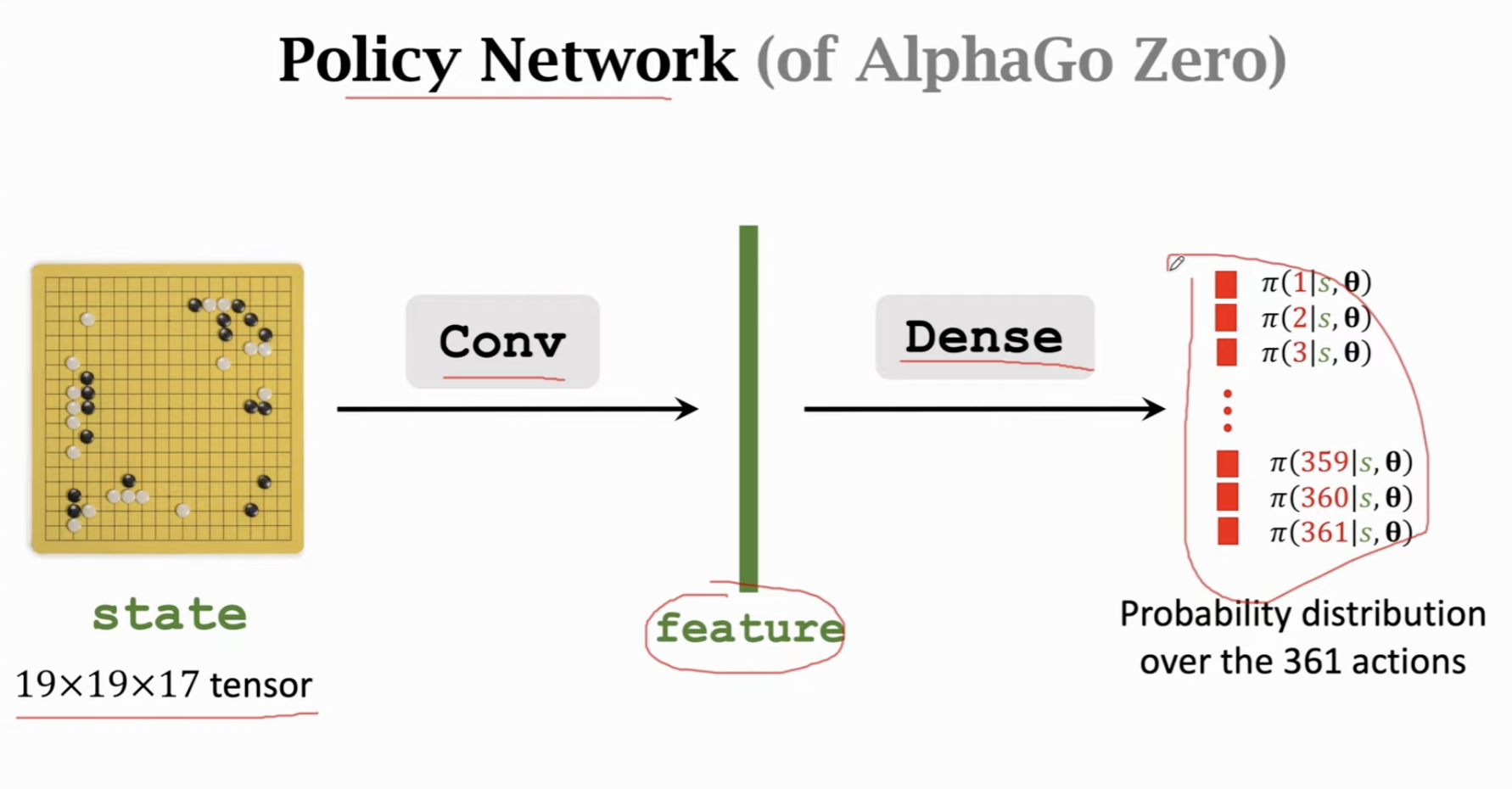
通过神经网络（policy network）近似策略函数，需要用到policy gradient算法。
策略函数：\(\pi(a|s)\)是一个概率密度函数（PDF），需要满足概率密度函数的性质。
关键在于怎么得到这个函数。假如一个游戏状态和动作的数目都很少，可以直接画一个\(n\times m\)的表，直接把概率算出来即可。但是对于游戏这种场景，无法这样得到策略函数，需要学习一个函数来近似策略函数。
回顾：
这里的\(A\)被当作随机变量，概率密度函数是\(\pi\)，把\(A\)消掉后\(V_{\pi}(s_t)\)只和\(\pi\)和\(s_t\)有关，可以评价当前状态/策略的好坏。
通过神经网络近似策略网络\(\pi\)，进而近似\(V\)：
随机梯度，随机性来源于\(S\)
为什么梯度上升？因为想让\(V\)越来越大
Policy gradient
\(Q_{\pi}\)和\(\theta\)还是有关的，这里的推导并不严谨。
这里之所以这么做是要凑期望的形式？
对于连续变量，用第二种形式，用蒙特卡洛近似：
这里的\(\hat{a}\)是一个确定的动作。蒙特卡洛近似就是抽取一个或多个随机样本用于近似期望。这种方法对于离散动作也是适用的。
如何近似计算\(q_t\)？
REINFORCE算法：
REINFORCE算法需要玩完一局游戏，观察到所有奖励才能更新策略网络。
神经网络近似：actor-critic方法
4 基于价值的强化学习
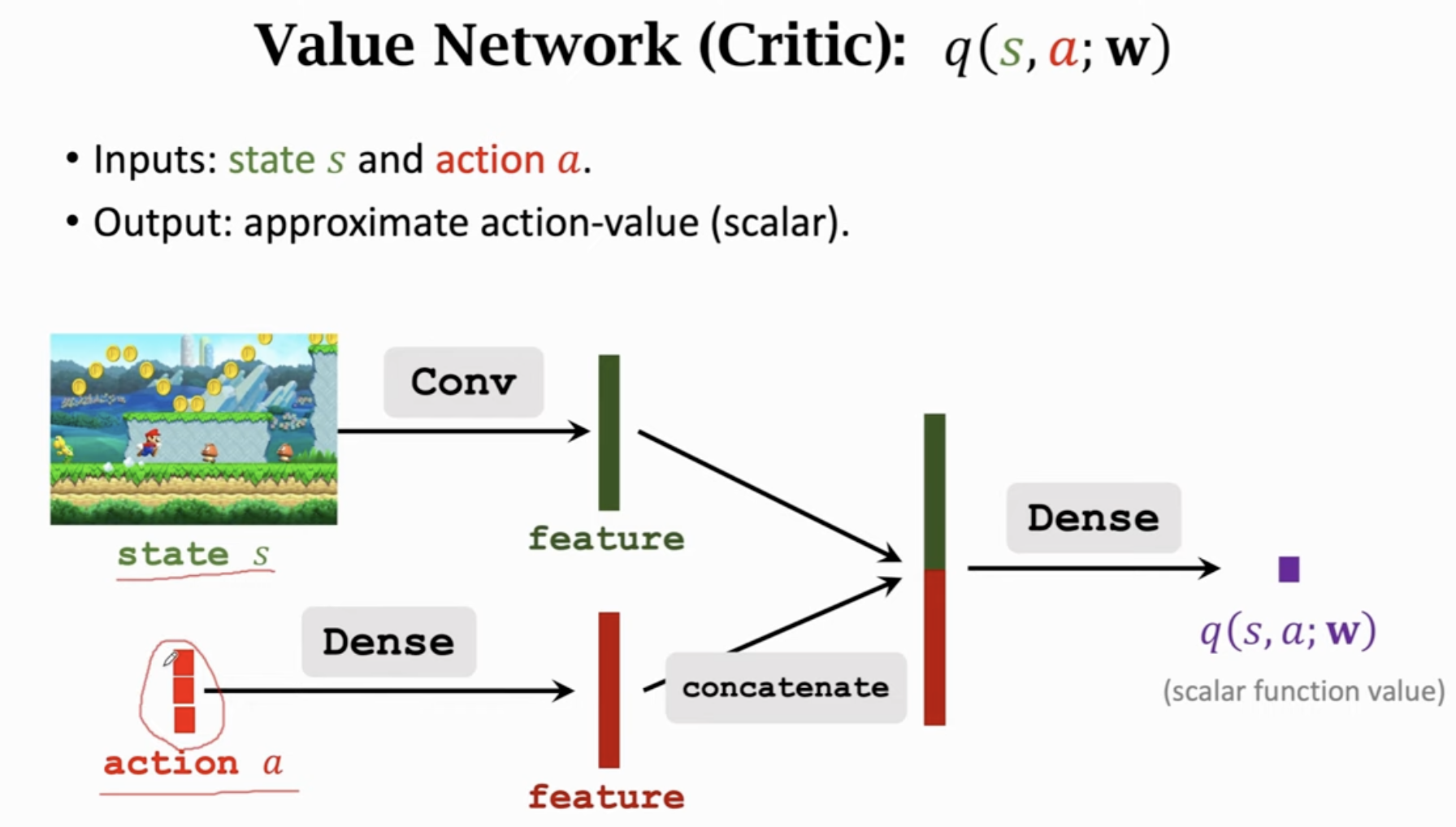
actor：策略网络，控制agent运动。critic：价值网络，用来给动作打分。构造两个网络，通过环境给的奖励去学习。
\(V_{\pi}\)是\(Q_{\pi}\)的期望。\(\pi\)和\(Q_{\pi}\)都不知道，可以通过两个神经网络同时学习这两个函数：
神经网络近似：\(V_{\pi}(s)=\Sigma_a\pi(a|s)\cdot Q_{\pi}(s,a)\approx \Sigma_a\pi(a|s;\boldsymbol{\theta})\cdot q(s, a; \boldsymbol{w})\)
价值网络只是给动作打分，不控制agent的运动。
参数可以共享 or 独立。
网络训练：
actor靠critic打分改进动作，critic通过环境的reward改进打分水平。
可以使用TD算法更新价值网络\(q\)：
动作是根据策略网络\(\pi\)随机抽样得到的。
更新策略网络：
必须根据\(\pi\)进行随机抽样，否则保证不了无偏性。
每一次迭代执行如下9个步骤，只做一次动作，获得一次奖励，更新一次网络：
部分书和论文用\(\delta_t\)代替\(q_t\)(with baseline)：
期望完全相等，效果更好，用好的baseline可以降低方差，收敛更快。任何接近\(q_t\)的数都可以是baseline，但这不能是动作的函数。上面这种方式的baseline是\(r_t+\gamma \cdot q_{t+1}\)。
最终目标：学习策略网络。价值网络只是起到辅助作用。
5 AlphaGo & Model-Based RL
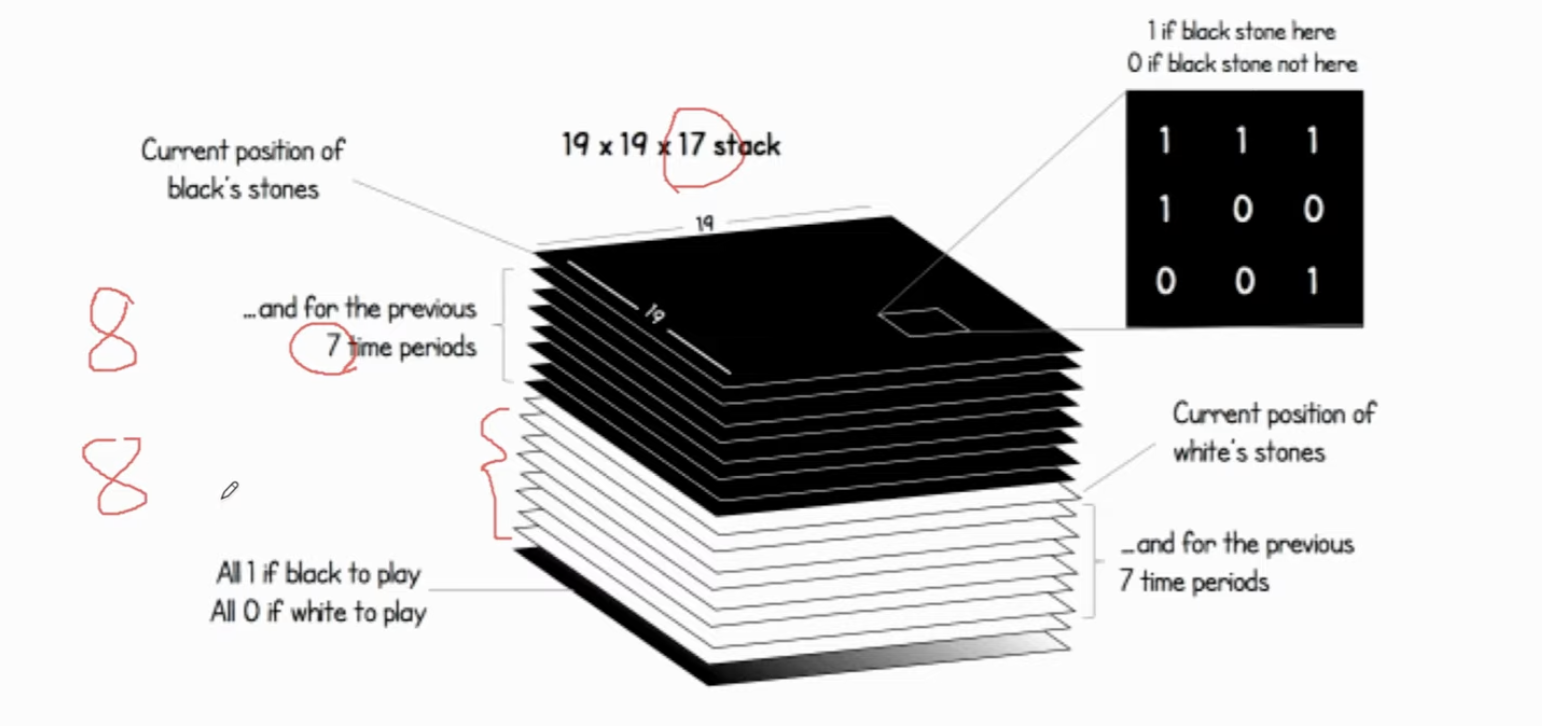
8+8+1=17
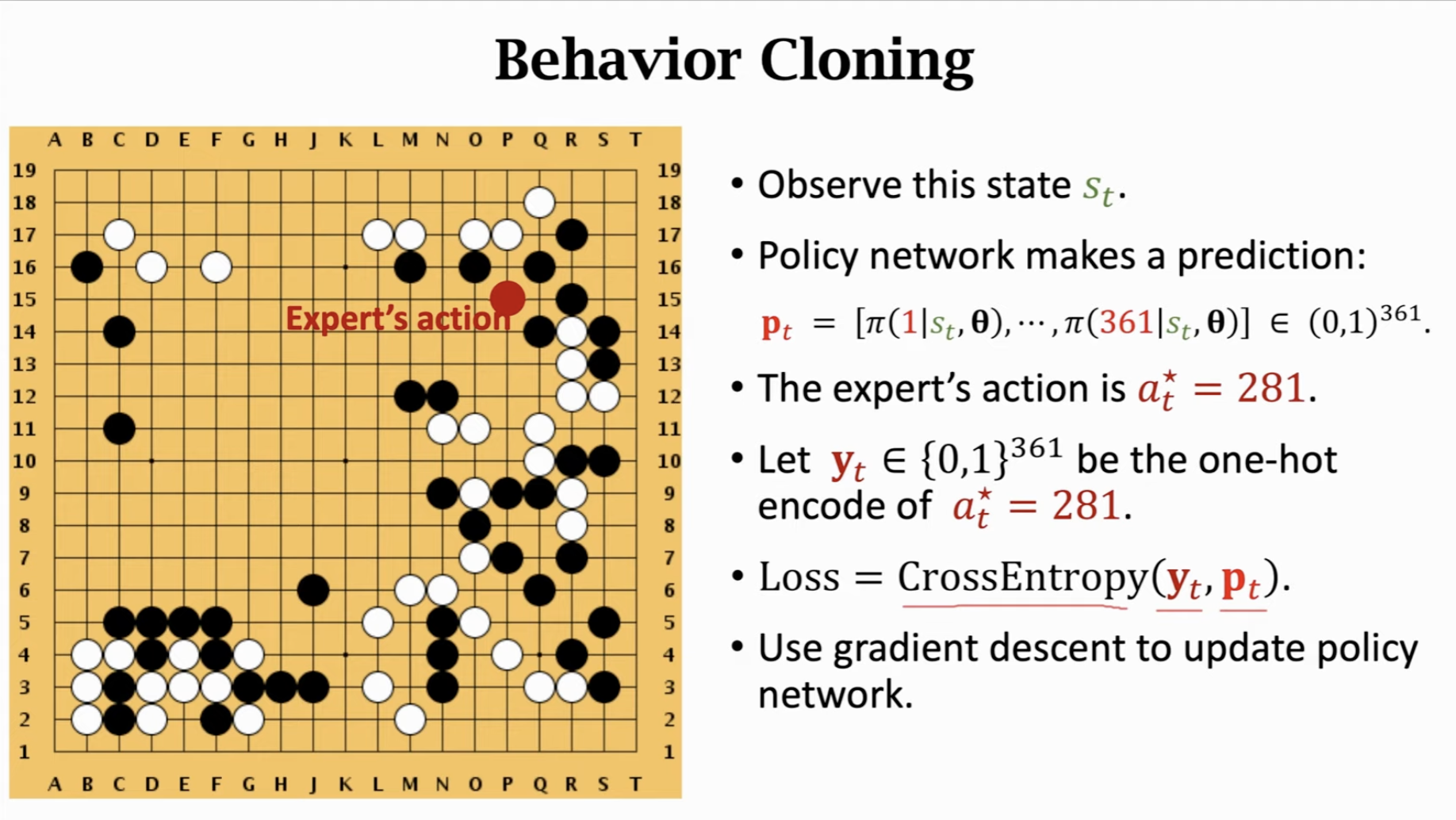
通过Behavior Cloning初始化Policy Network
最新的alpha-go zero没有用behavior cloning。
强化学习和模仿学习的本质区别在于有没有奖励。
实际上就是多分类任务：
可能存在错误累加的问题；围棋状态太多，很有可能遇到棋谱没有的动作；打败behavior cloning训练的ai，可以使用一些不同寻常的动作，使状态很特殊，不同于已有的棋谱。
Train Policy Network Using Policy Gradient
每下完一局，把胜负作为奖励，靠奖励更新player的参数。Opponent相当于环境，参数不用学习。
没有办法区分游戏里哪一部分是好棋，因此不作折扣。
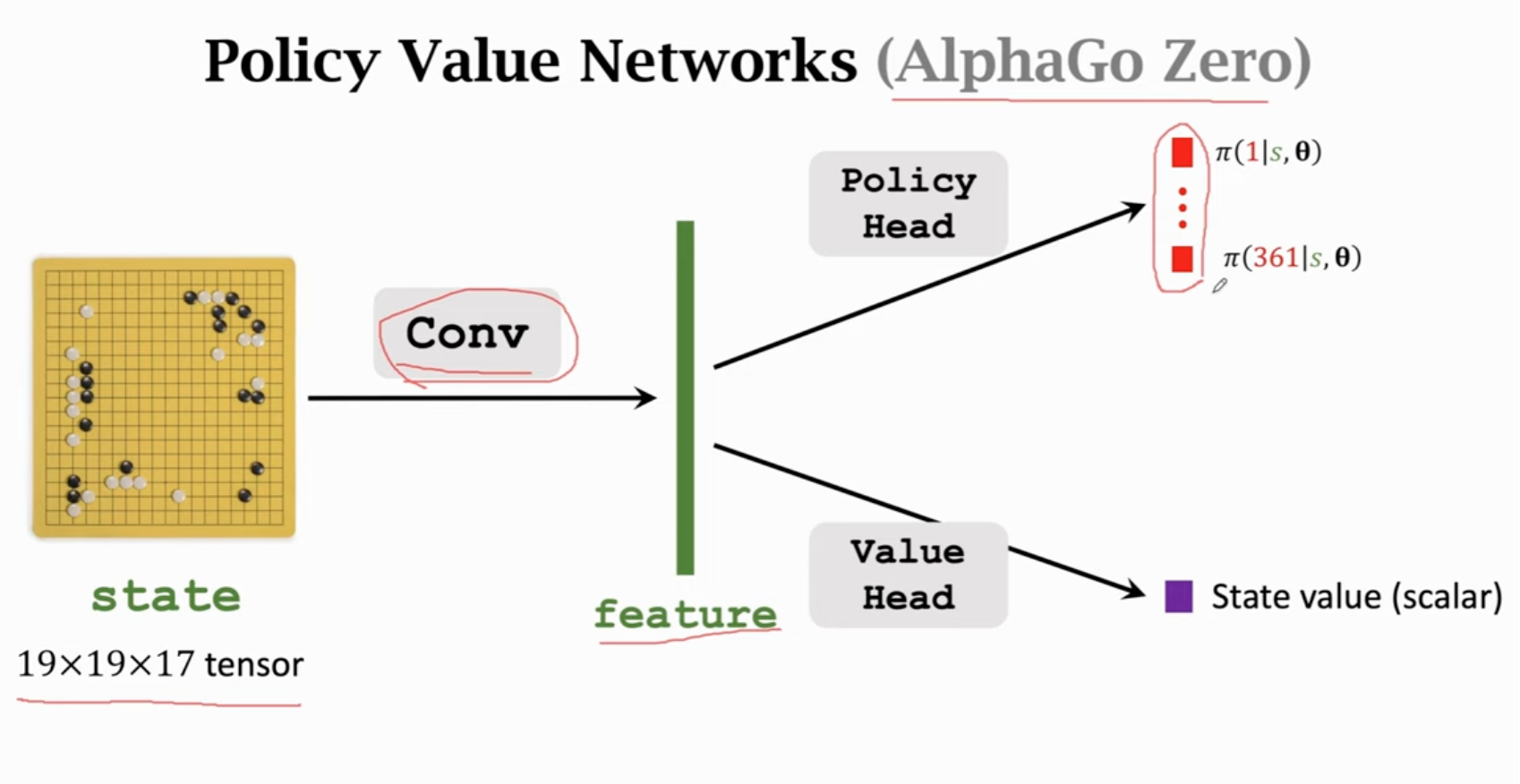
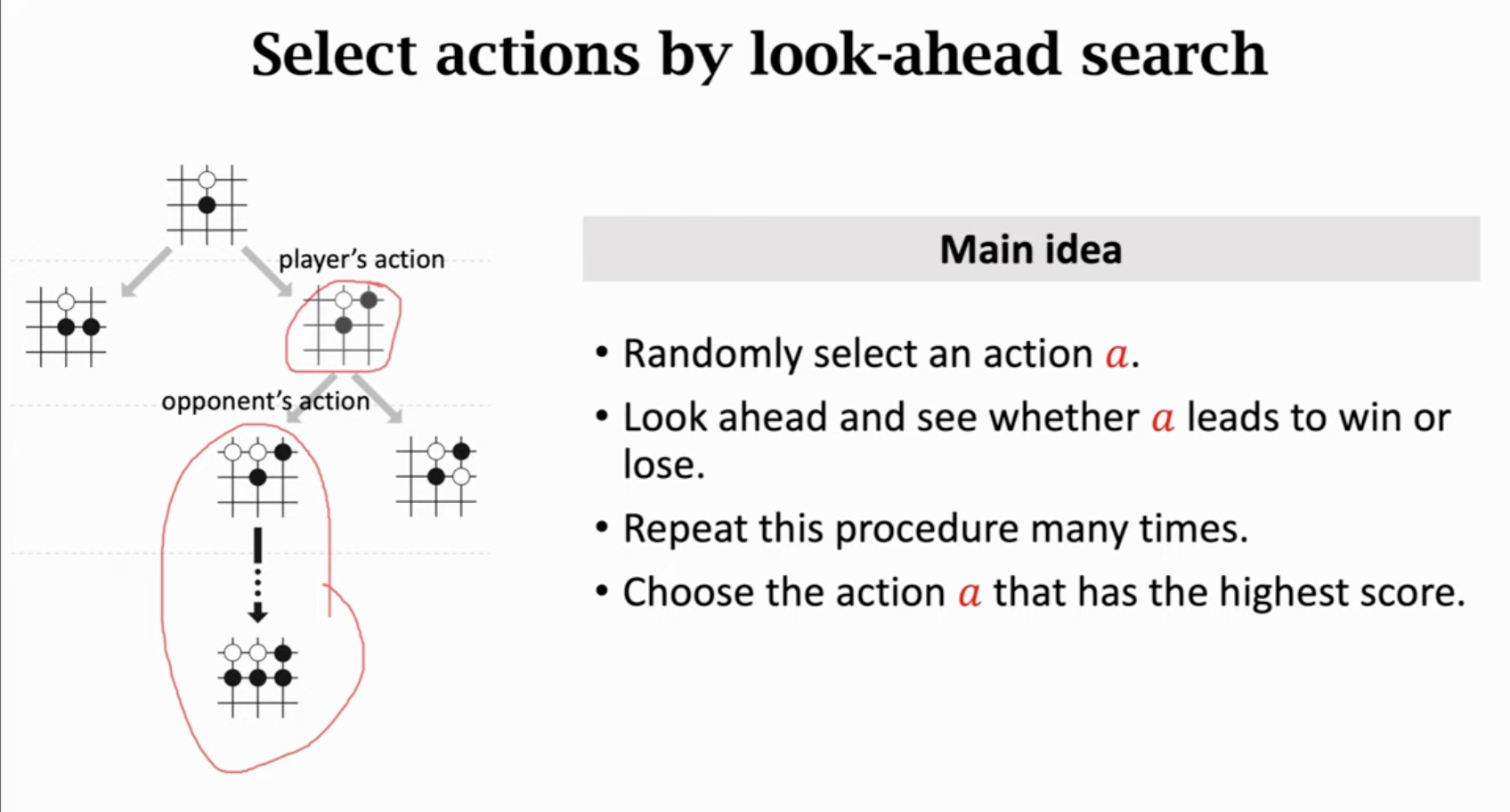
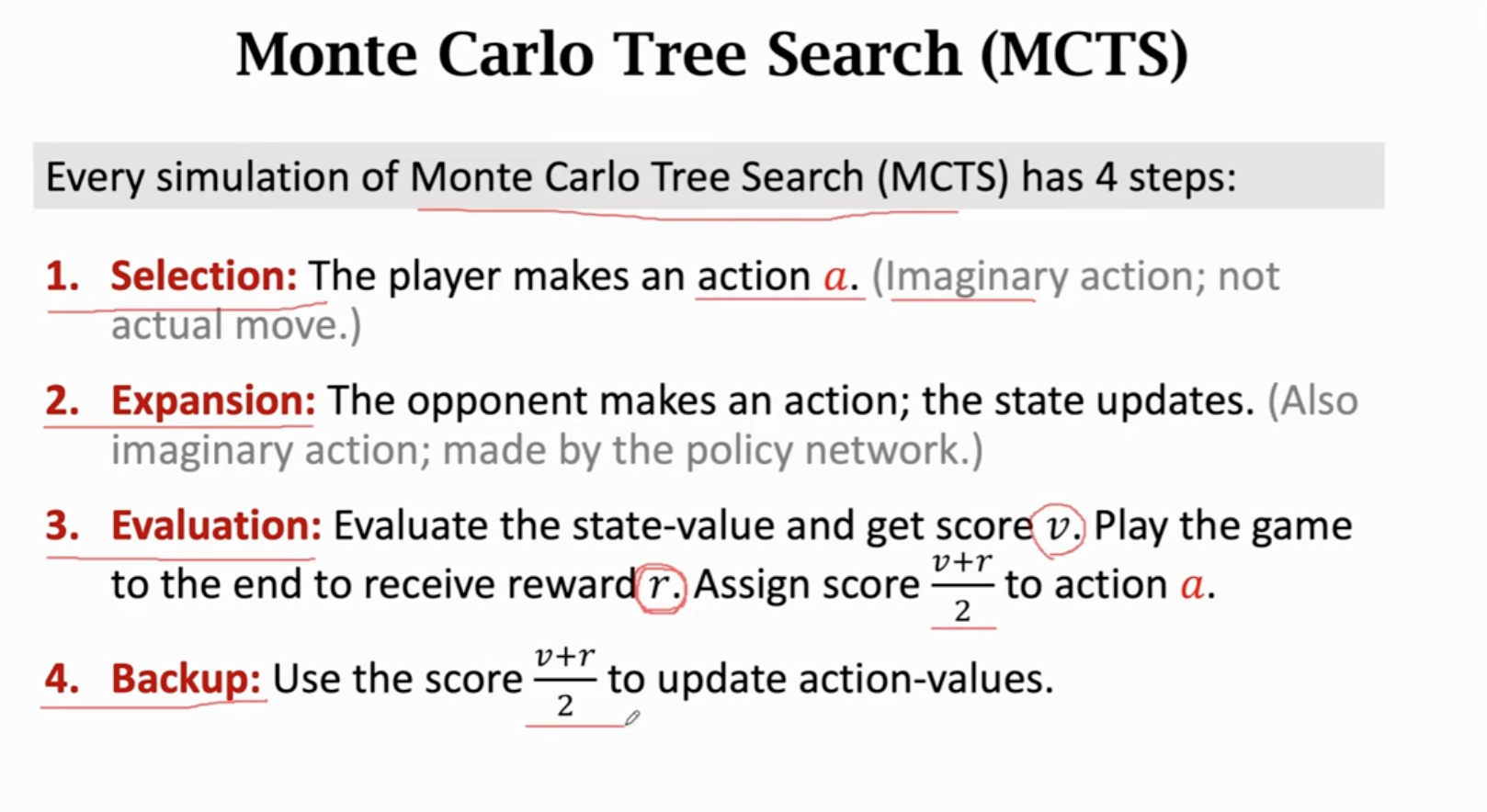
更好的是蒙特卡洛树搜索。为了实现蒙特卡洛树搜索，还需要训练一个价值网络。
先训练策略网络，再训练价值网络（不是actor-critic方法）：
训练过程中，通过训好的策略网络控制Player进行决策。
训练好AlphaGo之后，实际下棋的过程中，采用蒙特卡洛树搜索（无需训练）进行决策。
