SHARPNESS-AWARE MINIMIZATION FOR EFFICIENTLY IMPROVING GENERALIZATION论文阅读笔记
Intro
在训练集上最小化损失很可能导致泛化性低,因为当今模型的过参数化会导致training loss的landscape异常复杂且非凸,包含很多local/global minima,因此优化器的选择至关重要。loss landscape的几何性质(特别是minima的flatness)与泛化性有着紧密的联系,为此作者提出了SAM(Sharpness-Aware Minimization),通过寻找位于具有一致低损失值的邻域中的参数(而不是仅本身具有低损失值的参数)以提升模型的泛化性。
SHARPNESS-AWARE MINIMIZATION (SAM)
令标量为,向量为,矩阵为,集合为,“定义为”表示为,给定来自分布的训练集,训练集的损失表示为,泛化误差表示为。
由于模型只能看到训练集,因此通常的做法是让训练损失近可能小,然而这可能导致测试时的性能不佳。为此作者提出了SAM,不去寻找带来最小训练损失的参数,而是寻找整个邻域都具有一致低训练损失的参数值(邻域具有低损失和低曲率)。
Theorem (stated informally) 1.
对于任意,生成的训练集大概率满足:
其中是严格单调递增函数。证明位于附录A。
因此,为了使泛化损失近可能小,我们可以近可能减小其上界,而右边的项带有一个max,所以这构成了一个min-max问题。为了明确和sharpness有关的项,可以将不等式右边写为:
中括号中的部分表示的就是的锐度。鉴于右边的函数很大程度上受到证明细节的影响,这里作者将其写为标准的正则化项,通过超参数加以控制。由此,作者提出通过求解SharpnessAware Minimization问题来进行参数的选择:
其中,为超参数,(的值取2是最优的)。
为了最小化,作者通过对inner maximization求微分来得到的近似,这让我们能够通过SGD实现SAM的优化目标。为此,作者首先对在进行一阶泰勒展开:
优化问题的解可以通过求解经典的对偶范数问题得到:
其中。代入这个最优的值() 计算,之后将其回代到前面的公式,可以得到:
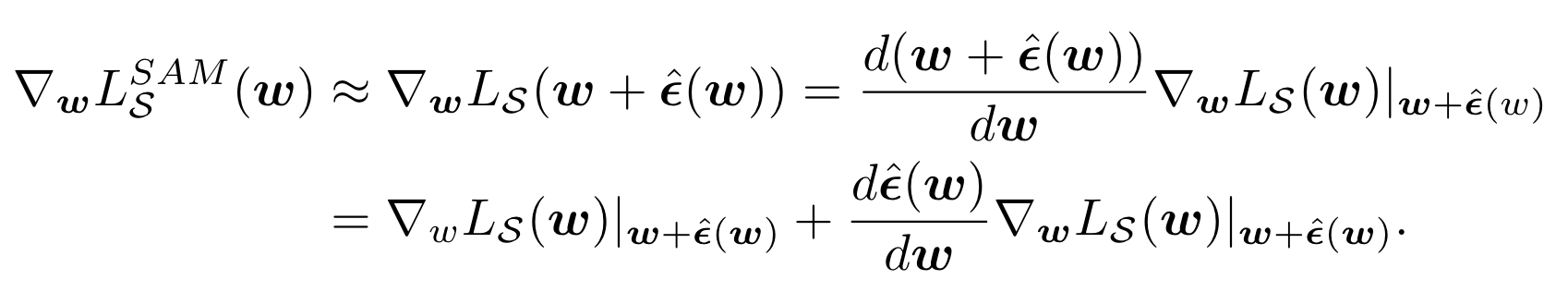
其中第二个等号通过复合微分的运算法则得到。为了加速计算,将二阶项丢掉,就可以得到最后的梯度近似:
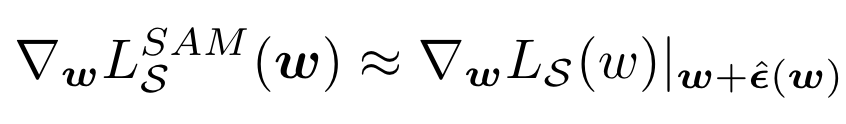
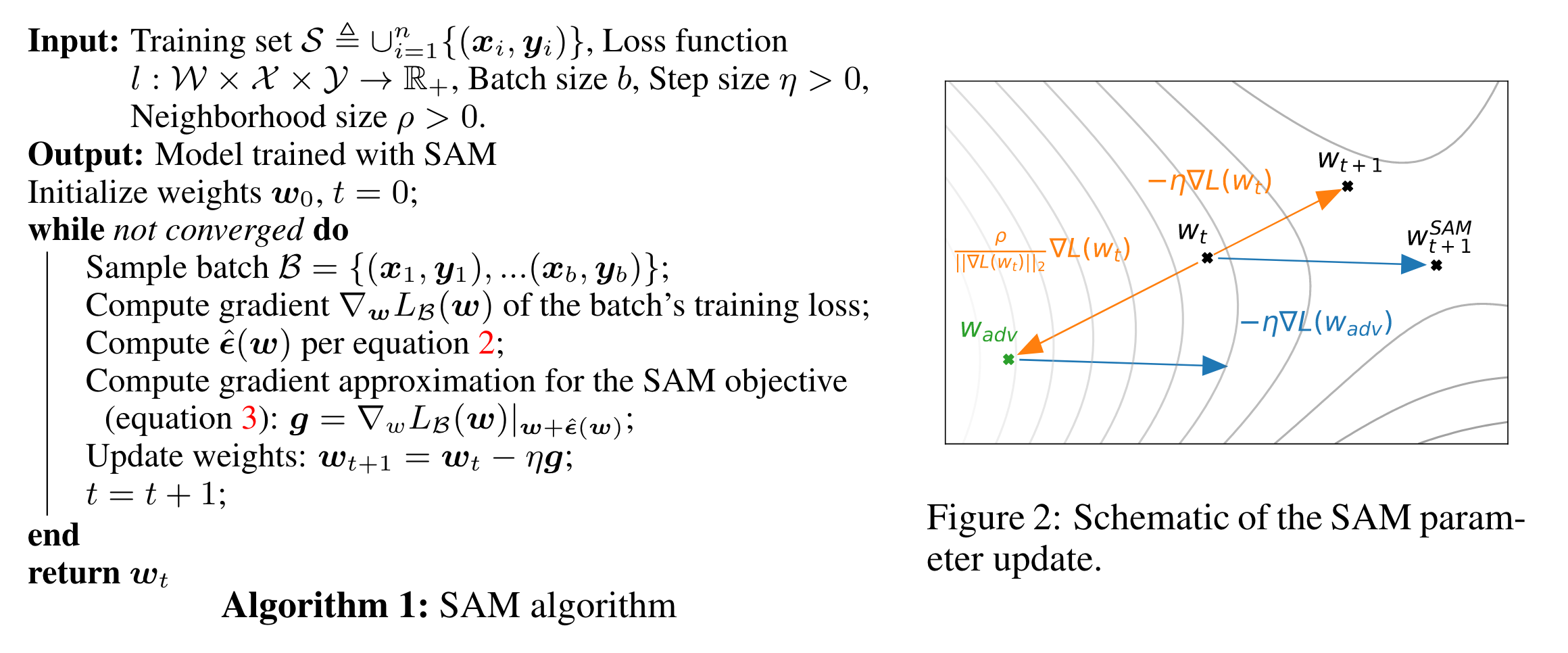
伪代码和示意图:
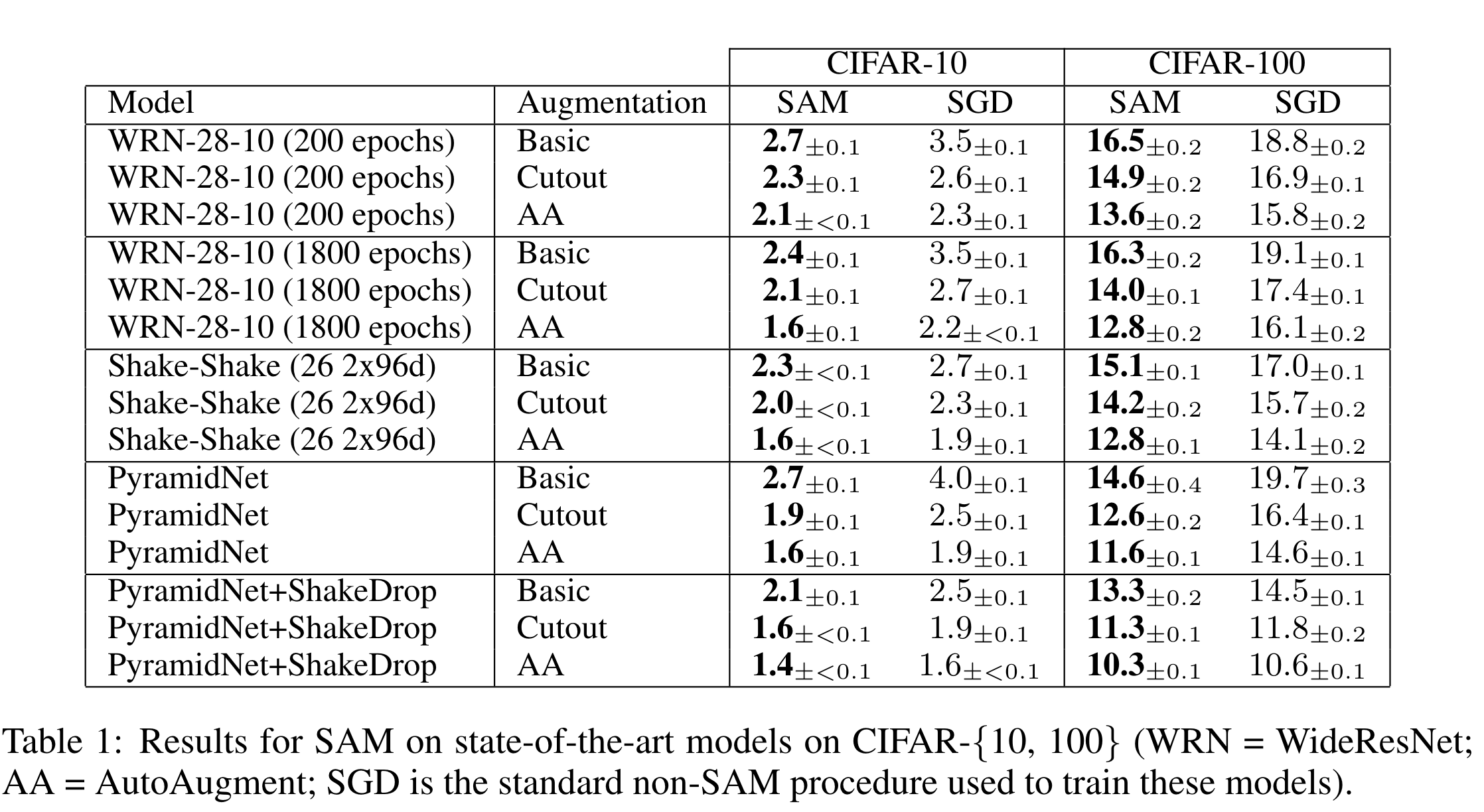
实验
等等
参考:https://blog.csdn.net/qq_40744423/article/details/121570423



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!
2023-01-13 学术规范与论文写作1&2