GMMSeg: Gaussian Mixture based Generative Semantic Segmentation Models
前置知识:【EM算法深度解析 - CSDN App】http://t.csdnimg.cn/r6TXM
Motivation
目前的语义分割通常采用判别式分类器,然而这存在三个问题:这种方式仅仅学习了决策边界,而没有对数据分布进行建模;每个类仅学习一个向量,没有考虑到类内差异;OOD数据效果不好。生成式分类器通过对联合分布建模,可以很好地解决这些问题。
为此,本文提出了基于GMM的分割框架GMMSeg,从而建模每个类的数据分布,借助(Sinkhorn) EM算法优化分类器,能够做到对大多数分割方法即插即用。
Method
不同于对后验概率进行建模,生成式分类器通过贝叶斯定理预测标签,通过估计类别条件分布以及类别先验对联合分布进行建模。后验概率可以表示为:。通常设置为均匀分布,因此核心在于估计。通过逼近数据分布优化生成式分类器的方式也叫做生成式训练。
本文提出的GMMSeg使用了M个多变量高斯分布加权去近似D维编码空间的每个类别:
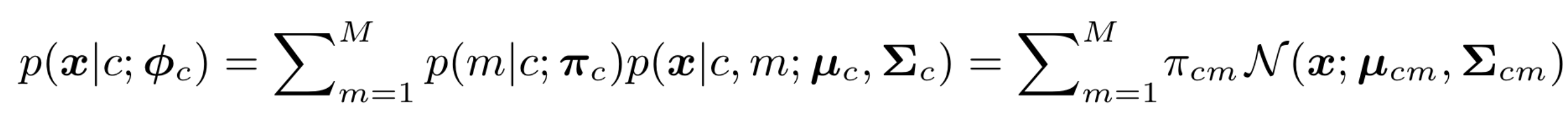
其中是先验概率(),最右侧就是GMM的形式。为高斯分布的参数。
优化GMM的标准做法是使用EM算法,最大化训练集中特征-标签集合的对数似然:
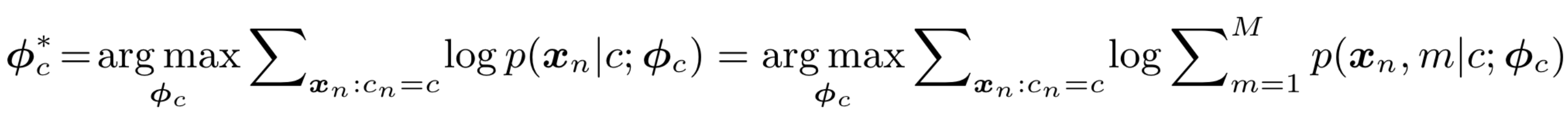
EM算法:
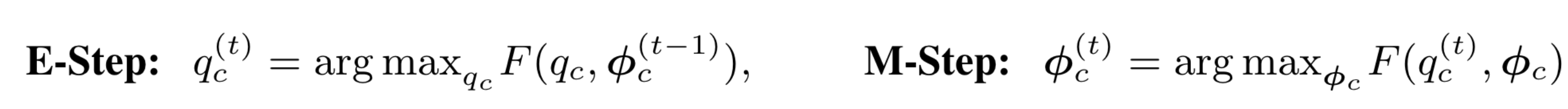
其中表示数据分到第m个高斯分量的概率,也就是EM算法中的Q函数。
F:
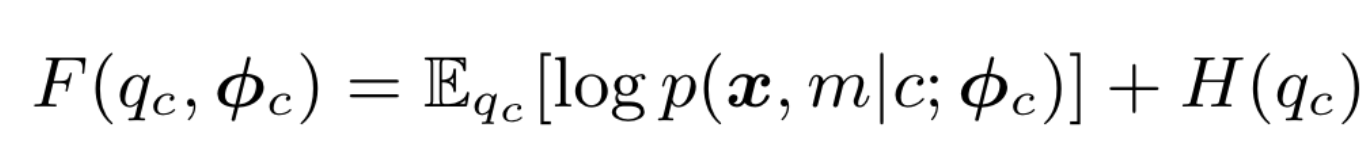
作者发现标准的EM算法收敛较慢且效果不好,可能的原因为EM算法对于参数的初始值敏感。考虑到基于最优传输的聚类算法,作者将均匀分布先验引入高GMM的权重:。这可以直观地看成是一个等分约束引导的聚类过程:在每个类别 c 中,我们希望 个像素样本被平均分配到 个高斯分布中。这样E step可以看做熵正则最优传输问题:
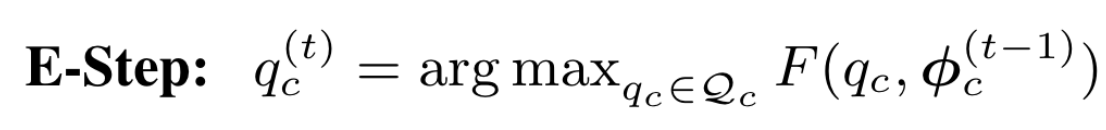
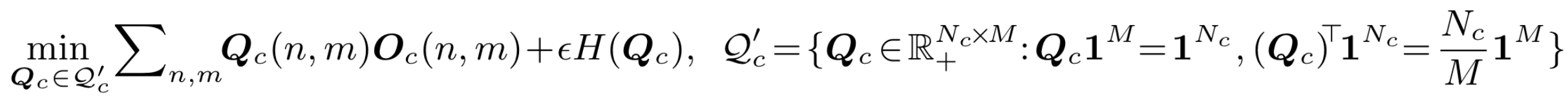
其中传输矩阵可以视作个样本对于个高斯分布的后验分布()。这种优化的方式被称为Sinkhorn EM,能够更好地避开local minima。
训练:分为两部分,分别优化GMM分类器以及特征提取器,

具体的细节见论文。
推理:将提取的特征带入GMM,计算该像素属于当前类别分布的似然,取最大值对应的类别作为结果。

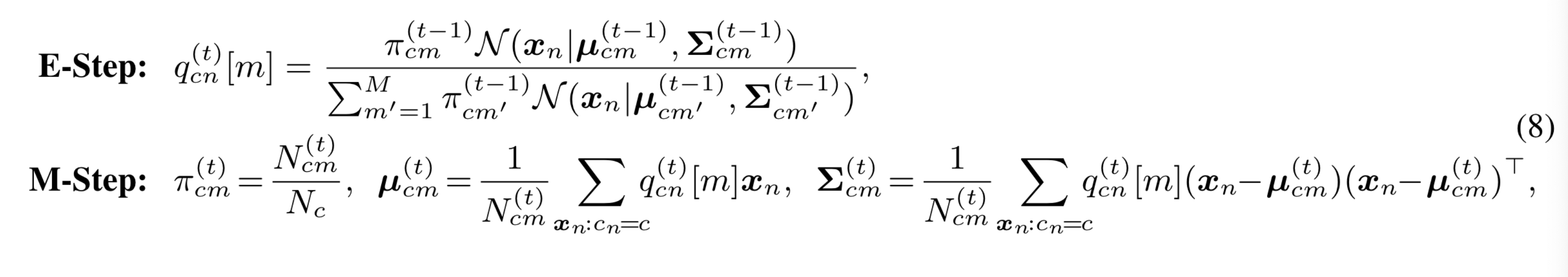


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!
2022-12-07 PyTorch单机多卡分布式训练卡死(已解决,原因未知)
2022-12-07 RuntimeError: Trying to backward through the graph a second time