Class-Incremental Learning with Generative Classifiers(CVPR2021W)
前置知识:VAE(可以参考https://zhuanlan.zhihu.com/p/348498294)
Motivation
之前的方法通常使用判别式分类器,对条件分布进行建模(classifier+softmax+ce)。其问题在于分类器会偏向最新学的类别,导致灾难性遗忘。
本文使用生成式分类器对联合概率分布进行建模(分解为),并使用贝叶斯法则进行分类。
:整个样本空间中,标签为y的样本的比例。
为什么有效:不会因为新的数据流产生偏差,仅有的分布会发生变化,而每个类别的样本数是可以统计的,或者可以假定所有标签有相同的先验概率(直接使用均匀分布建模)。
将class incremental learning转化为task incremental learning,每个task相当于为每个标签y学一个类别条件生成模型。
Method
作者使用VAE作为每个类别要学习的生成式分类器,通过重要性采样估计似然,使用均匀分布建模。
VAE包含一个encoder ,将输入变为隐空间的后验分布,decoder 通过隐变量得到输入空间的,还包含先验分布,其中encoder和decoder均使用神经网络:
优化目标:ELBO(evidence lower bound)
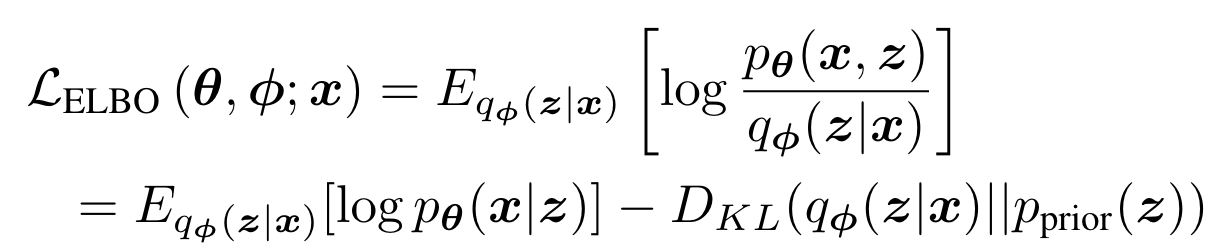
为了计算似然,作者使用了重要性采样(注意这里的VAE是针对某一个特定的类别y):
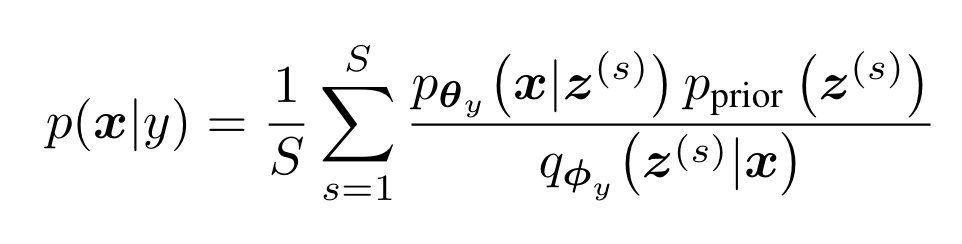
S代表采样样本数,代表第s个从采样出的样本。
基于贝叶斯定理 ,分类过程表示为:
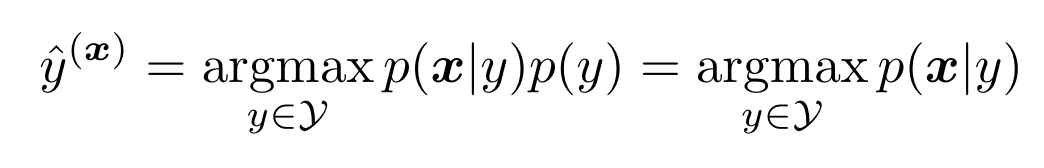
最后一步是由于本文直接使用均匀分布建模,保证了泛化性。
对于可以使用pretrained weight的情况,可以利用其直接初始化VAE的卷积层,也可以将pretrained model作为一个固定的特征提取器。

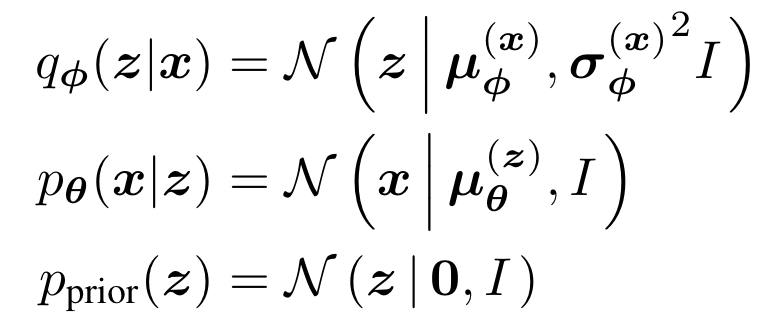


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!
2022-12-07 PyTorch单机多卡分布式训练卡死(已解决,原因未知)
2022-12-07 RuntimeError: Trying to backward through the graph a second time