[CVPR2022 Oral]Deep Rectangling for Image Stitching: A Learning Baseline论文阅读笔记
Deep Rectangling for Image Stitching: A Learning Baseline
1. 任务介绍
图像矩形化是将具有不规则形状图片(如多张图拼接而成的全景图像)变成一张矩形图片的方法。如果是找到一个最大的内接矩形进行裁剪,会损失较多的信息;图像补全填充的内容是基于预测的,其并不可靠,在一些对安全性要求较高的场景中(如无人车多摄像头拼接得到全景图)无法应用;图像矩形化则不会改变图片内容,仅仅是对原图进行拉伸。
传统的方法由kaiming大神发表在Siggraph 2013上,其主要分为两个阶段:Local warping和Global warping。一阶段是借助seam carving算法在原图上放置一个网格,这个网格有将原图拉伸为矩形的能力;第二阶段是通过设置三个能量项,通过优化这个能量函数使mesh产生一定的形变得到一个矩形mesh,最后将图片根据两个mesh的对应关系进行warp操作就能得到最终的结果。
原始方法(Kaiming)存在的几个问题:传统方法的初始mesh和最终mesh都是具有不规则形状的,这样在mesh的warp操作中无法进行矩阵加速。同时,该算法受限于LSD检测的性能同时也无法提取有效的语义感知特征,对结构复杂的场景并不鲁棒,其结果往往呈现出部分扭曲.
2. 提出的方法
区别于传统方法,作者设计了一种一阶段的rectangling策略。首先预先定义好了target mesh的形状为一个刚性的规则矩形,然后任务被简化为了只需预测一个初始的mesh,从初始的mesh到目标刚性mesh进行插值就可以通过矩阵运算加速了。为了实现这一点,作者设计了一个简单的神经网络从数据中学习如何预测mesh。
2.1 数据集
作者构建了一个数据集DIR-D用于测试。一个简单的想法是收集大量的全景图,然后通过传统方法拉伸为矩形图作为label。但这样有一个致命的缺点,意味着训练出来的网络的性能最终只能逼近传统的方法。因此作者使用了一种方法,保留用传统方法进行矩形化时的warp操作,随后对矩形图片进行warp逆变换得到构造出来的“全景拼接图”。为了解决warp操作与图片不对应的情况(反向warp出来的图像产生失真,感知不自然),作者使用同一个warp操作作用于数十张图片,挑选效果较好的图片作为数据集的输入。
2.2 损失函数设计
作者设计了最简单的网络来验证idea是否work。网络整体是由几层卷积层和全连接层构成的一个回归网络,来预测初始网格的mesh形状。网络预测出来的是mesh格点的运动向量,根据最终定义的刚性mesh和这个运动向量就能获得初始的mesh,进而可以通过插值得到原图。
传统方法是通过设置三个能量项——形状保持项,线保持项以及边界保持项来优化网格。参考其思想,作者设置了三个损失函数,最终的损失函数为这三个损失函数的和。
2.2.1 Content term
这部分是像素层面的L1 Loss和感知层面的L2 Loss。前面是使用Label与warp后的图像求L1 Loss,后面是分别将Label与warp后的图像送入VGG19的conv4_2,得到的结果(含有高层的语义特征)求L2 Loss。和都是可学习的参数。
2.2.2 Mesh term
网格内约束的是网格每条边的长度需要大于一个阈值,如果不加以约束的话可能会导致图像出现非常剧烈的变化。
网格间的约束项约束的是相邻横向或者纵向的三个顶点要尽可能共线。这样是为了避免直线变成折线。
2.2.3 Boundary term
对于边界的约束是根据mask实现的。mask是一个二进制掩码图,如果对mask进行矩形化,最终得到的应该是一个全白的图。这里的E就是全为1的矩阵。
2.3 网络结构设计
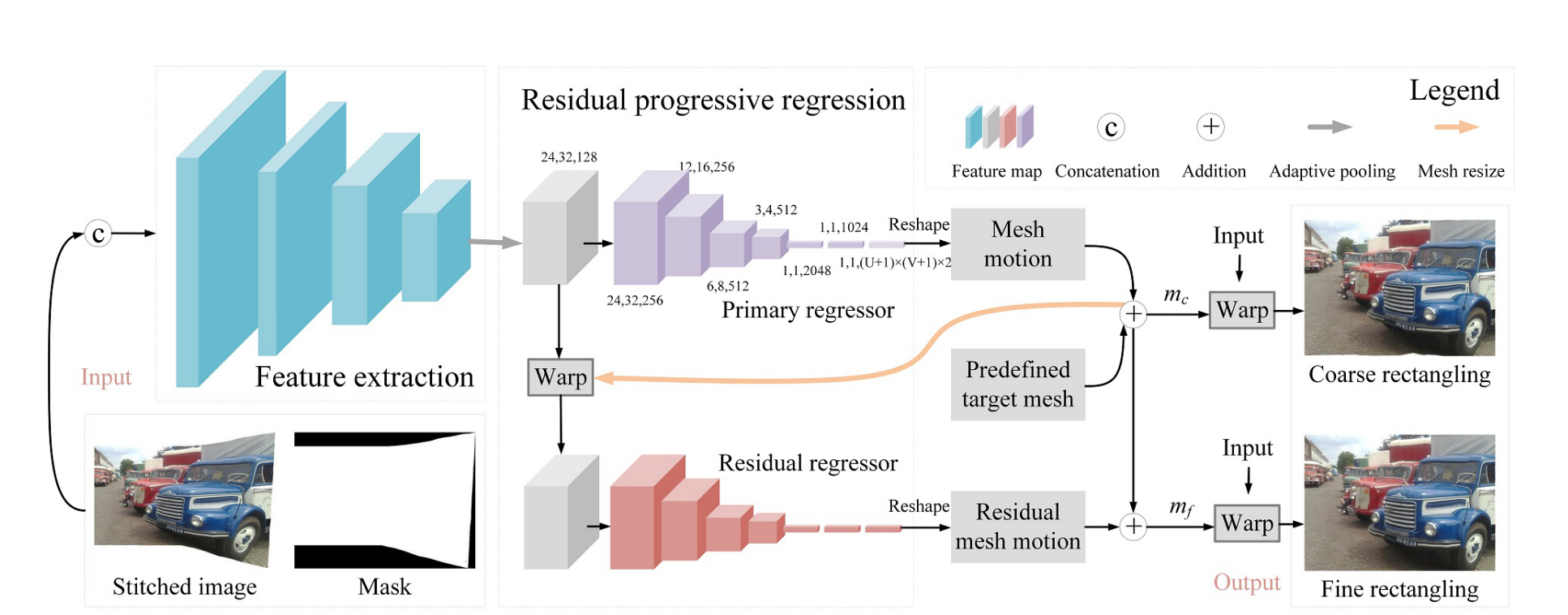 首先将拼接图和mask进行concat,通过卷积进行特征提取后得到特征图。之后通过一个简单的回归网络得到一个初始的Mesh motion,与预先定义的刚性target mesh相加就能得到初始的mesh。此时利用这个初始mesh对之前提取得到的特征图进行warp操作,得到的结果再送入回归网络,就能得到残差mesh motion,用这个mesh motion与第一次得到的初始mesh相加就能得到最终要输出的残差mesh。
首先将拼接图和mask进行concat,通过卷积进行特征提取后得到特征图。之后通过一个简单的回归网络得到一个初始的Mesh motion,与预先定义的刚性target mesh相加就能得到初始的mesh。此时利用这个初始mesh对之前提取得到的特征图进行warp操作,得到的结果再送入回归网络,就能得到残差mesh motion,用这个mesh motion与第一次得到的初始mesh相加就能得到最终要输出的残差mesh。
如果不设计残差回归的话,结果就像上面的第一次处理出来的图片,存在边缘不平整的问题。
3. 实验
作者定量实验的评价指标选取的是FID、SSIM以及PSNR。
FID是Fréchet Inception Distance,是图像生成任务的常用指标,表示生成图像的多样性和质量。FID越小,则图像多样性越好,质量越好。对于我们的label,所有真实图片的提取的向量是服从一个分布的;对于warp得到的图片对应的高位向量特征也是服从一个分布的。如果两个分布相近,那么意味着矩形化效果很好。假如一个随机变量服从高斯分布,那么这个分布可以用一个均值和方差来确定。那么两个分布只要均值和方差相同,那么两个分布则相同。我们可以利用均值和方差来计算两个单变量高斯分布之间的距离。这里是多维度的分布,我们可以使用协方差矩阵来衡量多个维度之间的相关性,所以使用均值和协方差矩阵来计算两个高维分布之间的距离。
其他两个指标分别是PSNR(峰值信噪比)和SSIM(结构相似性)。可以参考:https://zhuanlan.zhihu.com/p/50757421
作者分析效果远远好于传统方法的原因:最终得到的结果不一定要接近label,只要内容不畸变,结果合理即可。因此,作者还做了无参的盲图像质量评估,评价指标选取BIQUE和NIQE,可以参考:https://www.jianshu.com/p/f8fd3a8e45a4


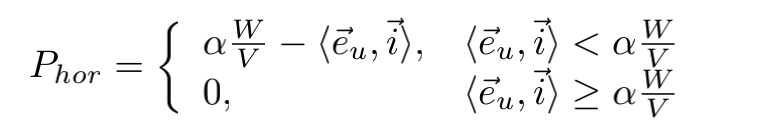
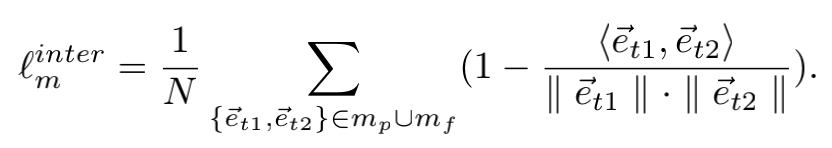
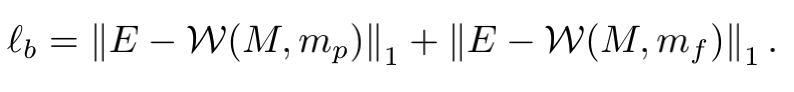



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!
2021-07-07 Leetcode 1711. 大餐计数(桶)
2020-07-07 SP1716 GSS3 - Can you answer these queries III(线段树)