贝叶斯估计
极大似然估计,概率空间(Ω,F,P),Ω代表元素,F代表σ-代数,P代表概率测度。X是随机变量,假定X∼p(x|θ)(密度函数中有θ作为参数),例如高斯分布等。将参数估计出来可以对随机变量有一个更好的理解。那么怎么去估计这个参数呢?进行独立抽样:x1,x2...xn,L(θ)=Πni=1(p(xi)|θ),极大似然估计想找到这样一个θ使得L(θ)最大,即argmaxθL(θ)。对其取log后就变成求和了,处理起来更加方便。
考虑二元伯努利分布,x1,...xn,xi∈{0,1}。p(X=xi)=p1−xi(1−p)xi。L(p)=p1−x1(1−p)x1...p1−xn(1−p)xn=pk(1−p)n−k。同样取对数后对p求导。这也可以拓展到多元的情况。
考虑高斯分布,N(μ,σ2),p(x)=1√2πσe−(x−μ2σ)2...极大似然估计给出的参数估计和一般的计算均值方差的方法算出来是一样的。
在极大似然估计中认为θ是一个参数,而在贝叶斯估计中认为θ是本身满足一定分布的随机变量。给定一组抽样S,p(θ|S)=p(S,θ)/p(S)=p(S|θ)p(θ)/p(S),在极大似然估计中关注的是p(S|θ)(认为θ是一个参数),而此时还需要把p(θ)乘上去。因此,argmaxθp(θ|S)=argmaxθp(S|θ)p(θ)p(S),注意到分母与θ无关,因此简化为:argmaxθp(S|θ)p(θ)。这里可以看出极大似然估计与贝叶斯估计的区别:是否乘以θ本身的分布。
应用:设θ满足(0,1)的均匀分布,则p(θ)恒等于1,argmaxθp(θ|S)=argmaxθp(S|θ)。
分类问题:
给出(x1,y1)...(xn,yn),xi∈Rk,yi∈{0,1}。出发点:把x,y看作联合分布,p(x|y=0)∼N(μ0,σ20),p(x|y=1)∼N(μ1,σ21)。对于一个新的样本,p(y=0|x)=p(y=0,x)p(x)=p(x|y=0)p(y=0)p(x,y=0)+p(x,y=1)=p(x|y=0)p(y=0)p(x|y=0)p(y=0)+p(x|y=1)p(y=1),p(x|y=0),p(x|y=1)已经能由我们的假设估计出来了,而p(y=0),p(y=1)也知道,因此就可以预测了。总之,问题就变成了估计μ0等这些参数。p(xi,yi)=p(xi|yi)p(yi)→Πni=1p(xi,yi)Πni=1p(xi|yi)Πni=1p(yi)。取对数后:Σni=1logp(xi,yi)=Σni=1logp(xi|yi)+Σni=1logp(yi)。与想要预测的参数密切相关的就是Σyi=0logp(xi|yi=0)+Σyi=1logp(xi|yi=1)这两项。μ0的最佳估计是Σyi=0xik,σ20的最佳估计是1kΣyi=0(xi−μ0)2,μ1的最佳估计是Σyj=1xjn−k,σ20的最佳估计是1n−kΣyj=1(xj−μ1)2。
对于分界线: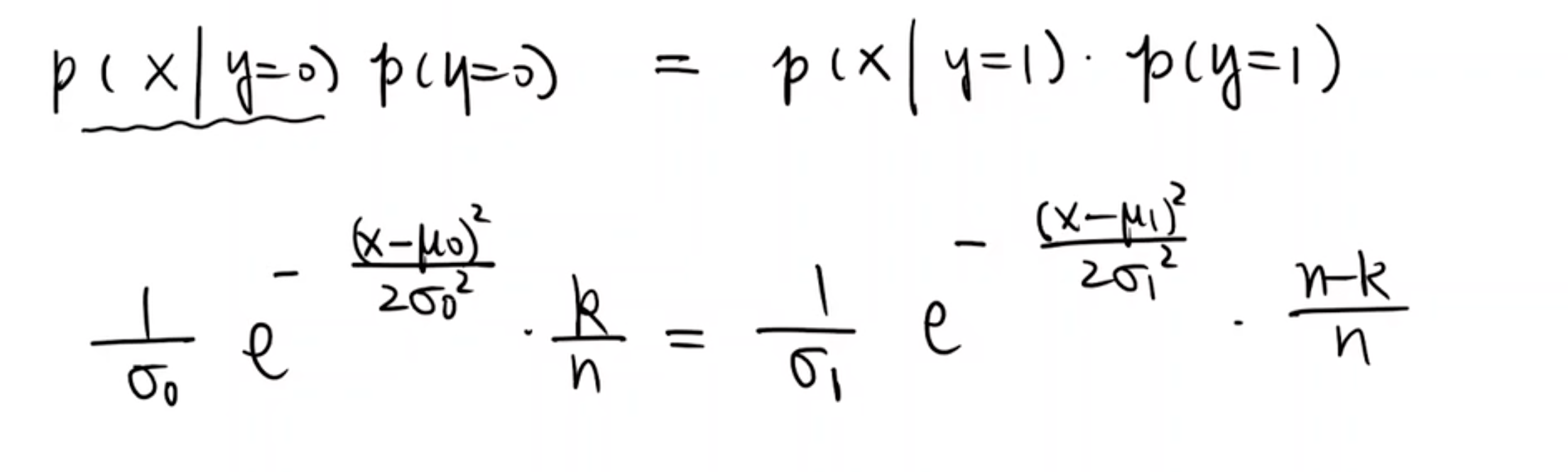
当σ0=σ1的时候,x是常数。

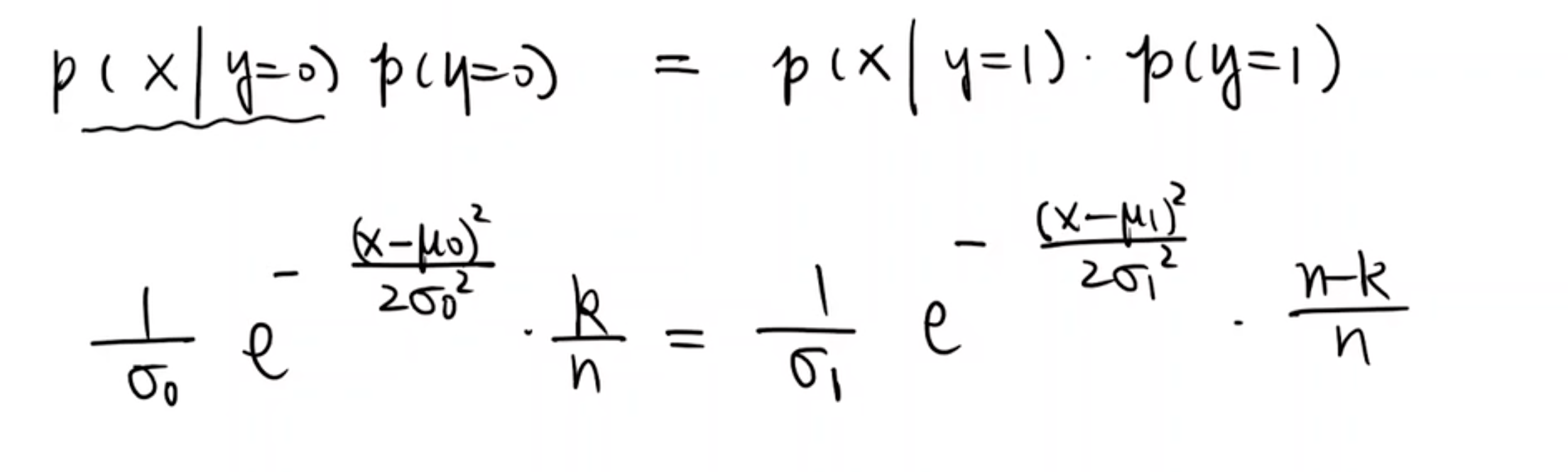


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek 开源周回顾「GitHub 热点速览」
· 物流快递公司核心技术能力-地址解析分单基础技术分享
· .NET 10首个预览版发布:重大改进与新特性概览!
· AI与.NET技术实操系列(二):开始使用ML.NET
· .NET10 - 预览版1新功能体验(一)
2020-04-11 NOIP 2017 提高组 DAY1 T1小凯的疑惑(二元一次不定方程)
2020-04-11 Educational Codeforces Round 85 B. Middle Class(排序/贪心/水题)
2020-04-11 Educational Codeforces Round 85 A. Level Statistics(水题)