Swin Transformer论文阅读笔记
Swin Transformer
Swin transformer是一个用了移动窗口的层级式(Hierarchical)transformer。其像卷积神经网络一样,也能做block以及层级式的特征提取。本篇博客结合网上的资料,对该论文进行学习。
摘要
本篇论文提出了一个新的Transformer,称作Swin Transformer,其可以作为计算机视觉领域的一个通用的骨干网络。这是因为ViT这篇论文仅仅是做了分类的任务, 而Swin Transformer在计算机视觉的各个领域都有取代CNN的潜力。但是直接把Transformer用到视觉方面会有两个问题:一个是视觉实体的尺度有很大的变化(比如无人驾驶任务中一张街景图片,此时代表同样语义的一个词其对应的实体可能有各种各样的大小,这种问题在NLP就不曾出现),另一个是图像的像素与文本中的字相比分辨率非常高,如果以像素点作为基本单位的话序列的长度就会迅速增加。针对第二个问题,目前的解决方案要么是以特征图作为输入,要么是把图片打成patch,要么是把图片画成一个个小窗口,在窗口里做自注意力。针对上述两个问题,作者 提出了一种包含移动窗口、具有层级设计的Transfoer——Swin Transformer。这种设计让两个相邻的窗口之间产生了交互(cross-window connection)。同时作者提到,这种分层结构可以灵活地在不同的尺度上建模,并且计算复杂度随着图像大小的增大而线性增长(非平方级别增长)。由于这种分层的结构,Swin Transformer像卷积神经网络一样拥有了多尺度的特征,因此可以被应用到下游任务中。
引言
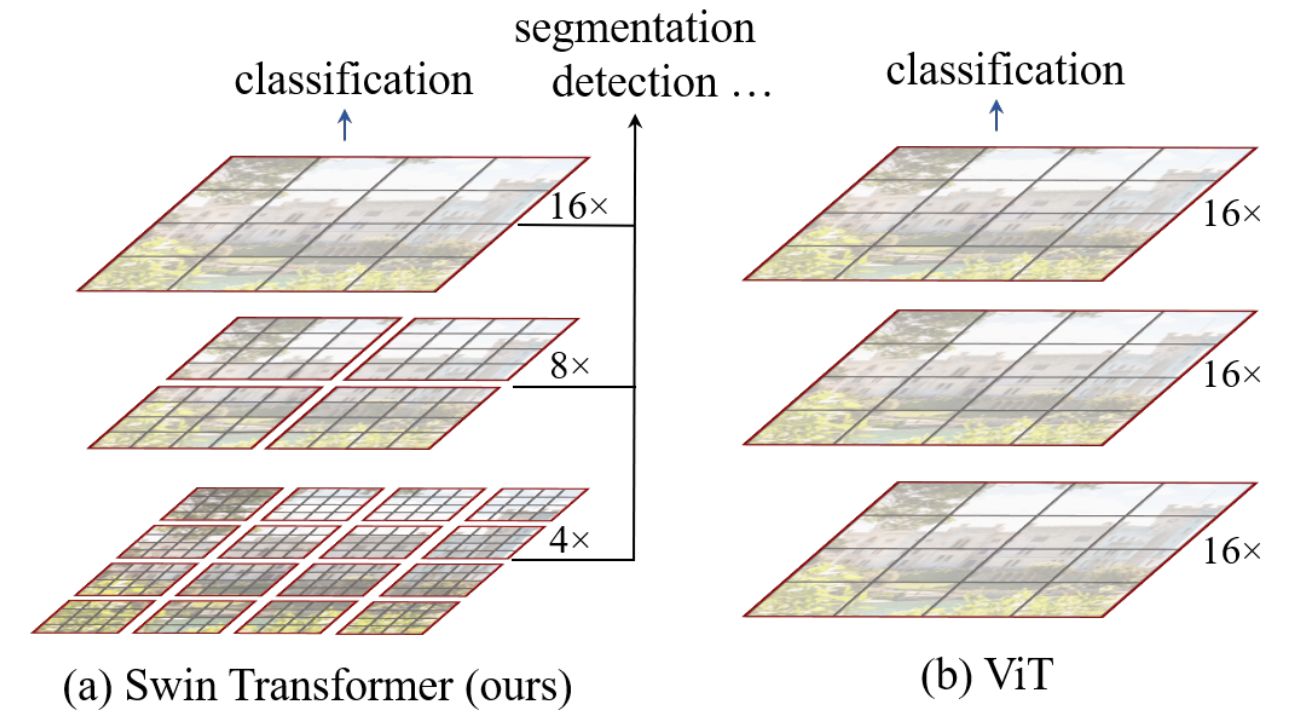
上图是Swin Transformer和ViT的一个对比。ViT每一层都是16倍的下采样率,不适用于预测密集型任务。同时其对于多尺度特征的把握会变弱,而对于检测和分割的任务,多尺度的特征是非常重要的。且其自注意力始终是在整张图上进行,即是一个全局建模,其计算复杂度与图像大小成二次方关系。因此,Swin Transformer借鉴了CNN的很多设计理念以及其先验知识:小窗口内算自注意力(认为同一个物体会出现在相邻的地方,因此小窗口算自注意力其实是够用的,而全局自注意力实际上有一些浪费资源)。CNN之所以能抓住多尺度的特征是因为池化这个操作(能增大每一个卷积核的感受野),因此Swin Transformer也提出了一个类似池化的操作,把相邻的小patch合成一个大的patch。
Swin Transformer最关键的一个设计元素就是移动窗口,使得窗口与窗口之间可以进行交互,再加上之后的patch merging,合并到transformer最后几层的时候每一个patch本身的感受野就已经很大了,再加上移动窗口的操作,就相当于实现了全局自注意力。
方法
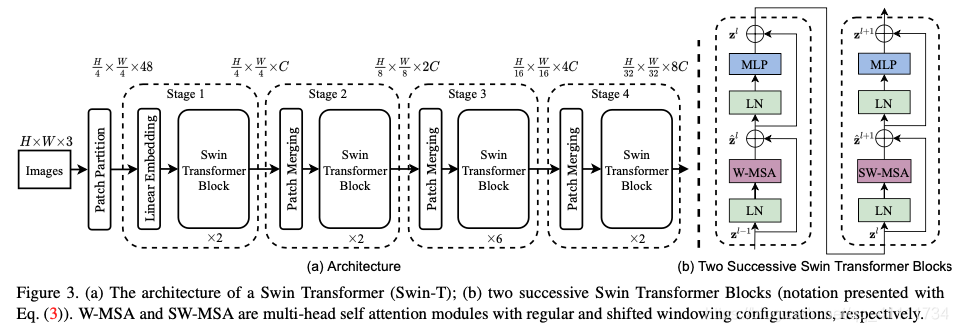
整体流程
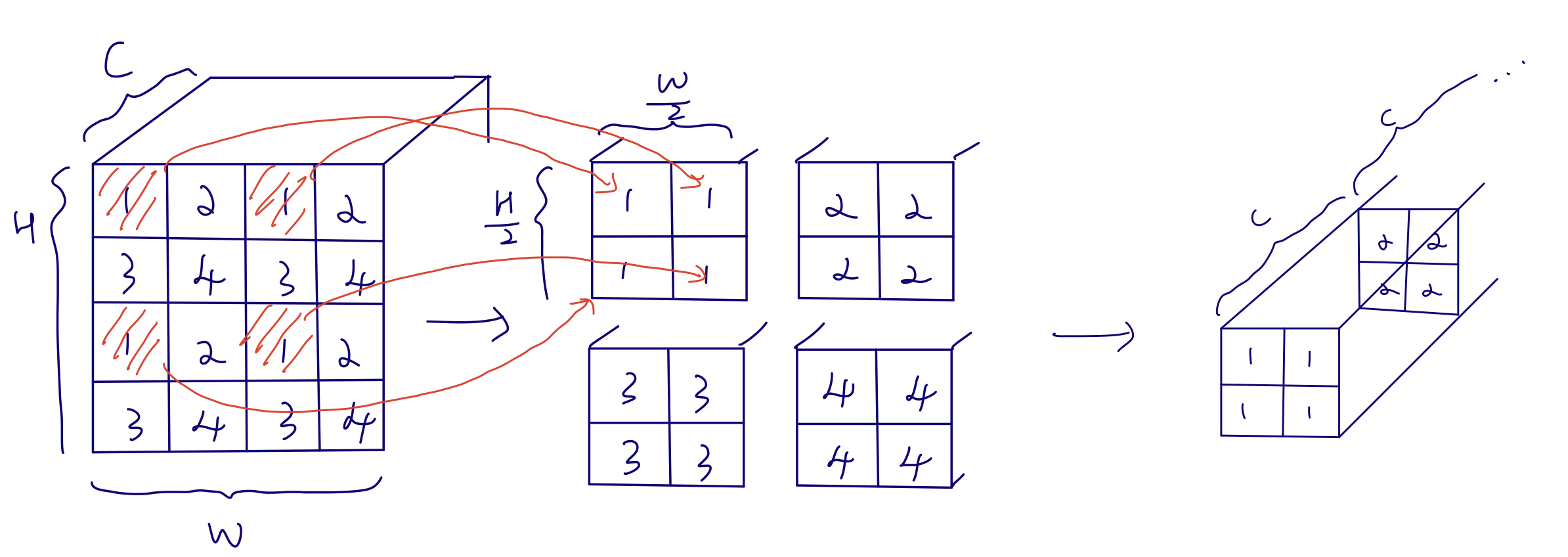
假设有一张ImageNet标准尺寸图片,首先将其打成patch(而非),得到的图片尺寸是,其中(3为通道数)。之后是Linear Embedding,把向量的维度变成Transformer能够接受的值,超参数设置为C。Swin-T的C为96,此处为。之后前两个56拉成一个维度(即seq的长度),之后的96变成了每一个token的向量的维度。而3136太长了,transformer不可接受,因此Swin Transformer Block使用了基于窗口的自注意力计算方法。对于每个窗口,其默认只有个patch,序列长度就变成了49,相比3136而言大大减小。如果对于transformer不做约束的话,输入序列长度是多少,则输出序列长度就是多少,因此经过第一个Block之后,输出的尺寸还是。之后为了实现层级的结构,需要加入类似CNN中池化的操作,因此就有了图中的Patch Merging。这里想要下采样两倍,因此经历了如下图的过程(最后将四个张量在通道维度拼接),向量变为(其中):
CNN中池化后通道数往往翻倍,因此这里也想要让其翻倍,而此时通道维是4C而非2C,因此需要用卷积核把通道维将为,所以经过第一个Patch Merging后向量大小为。之后再经历一个transformer block其大小不变,因此第二个stage结束后大小为。以此类推,第四个stage结束后输出大小为。
在最后,直接使用全局平均池化将变成1来做分类。然而Swin Transformer并非只做分类,因此这一部分可以修改,作者也就没有画出来。
基于自注意力的移动窗口
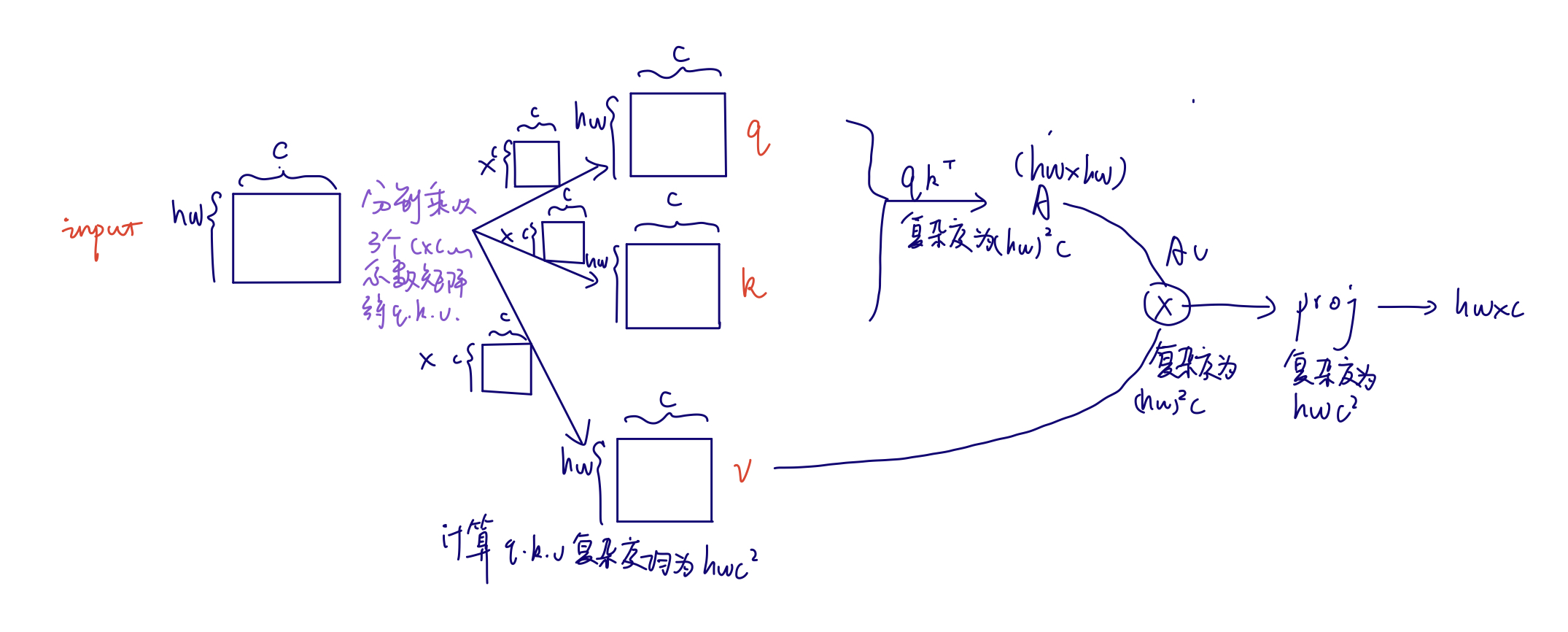
作者首先介绍了这样做的动,即全局自注意力计算会导致平方级别的计算复杂度,进而提到使用窗口来做自注意力。原来的图片会被平均分成没有重叠的窗口。以第一层输入为例,其大小为,将其切分为个窗口,每个窗口内有个patch(文章中M默认为7)。自注意力都是在小窗口完成的,序列长度永远为49。对于计算复杂度,作者进行了如下估计(假设划分为个patch):
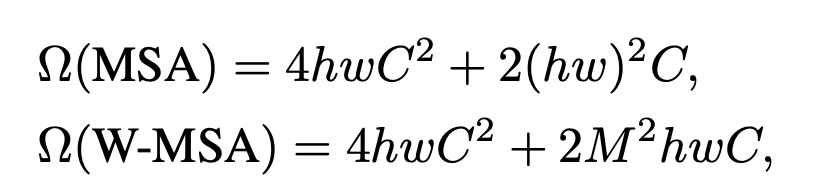
第一个公式是标准的多头自注意力,计算过程如下:
而对于使用窗口的多头自注意力,一个窗口内计算的还是多头自注意力,可以直接套用前一个公式,对于每个窗口,input大小变为(h和w变为m和m),因此一个窗口的计算复杂度为,而总共有个窗口,乘起来就是。
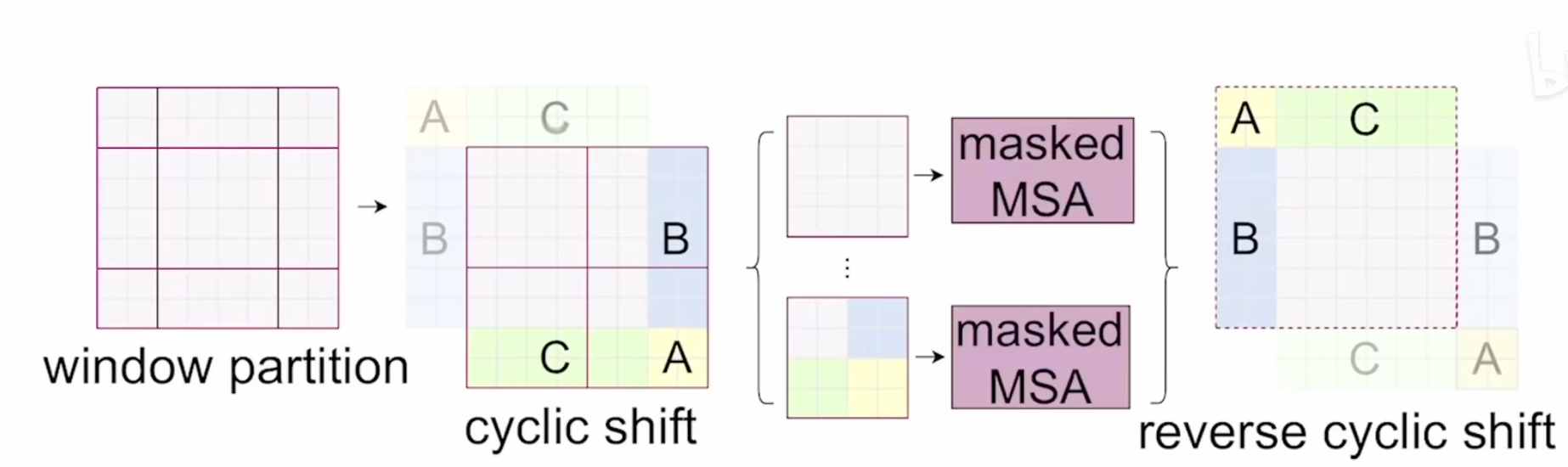
对于这种方式,作者说虽然这很好地解决了内存和计算量的问题,但是缺少了窗口和窗口之间的通信,会限制模型的表达能力。因此作者提出了移动窗口的方式。具体的过程参看下图:
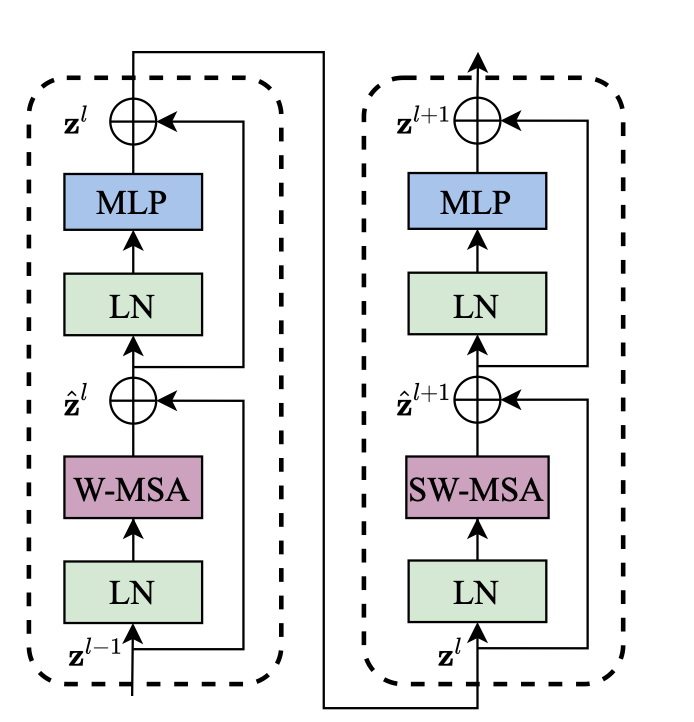
因为每次都是先做一次基于窗口的自注意力,再做一次基于移动窗口的自注意力,所以整体流程的图里Transformer Block的数量都是偶数(2、2、6、2)。
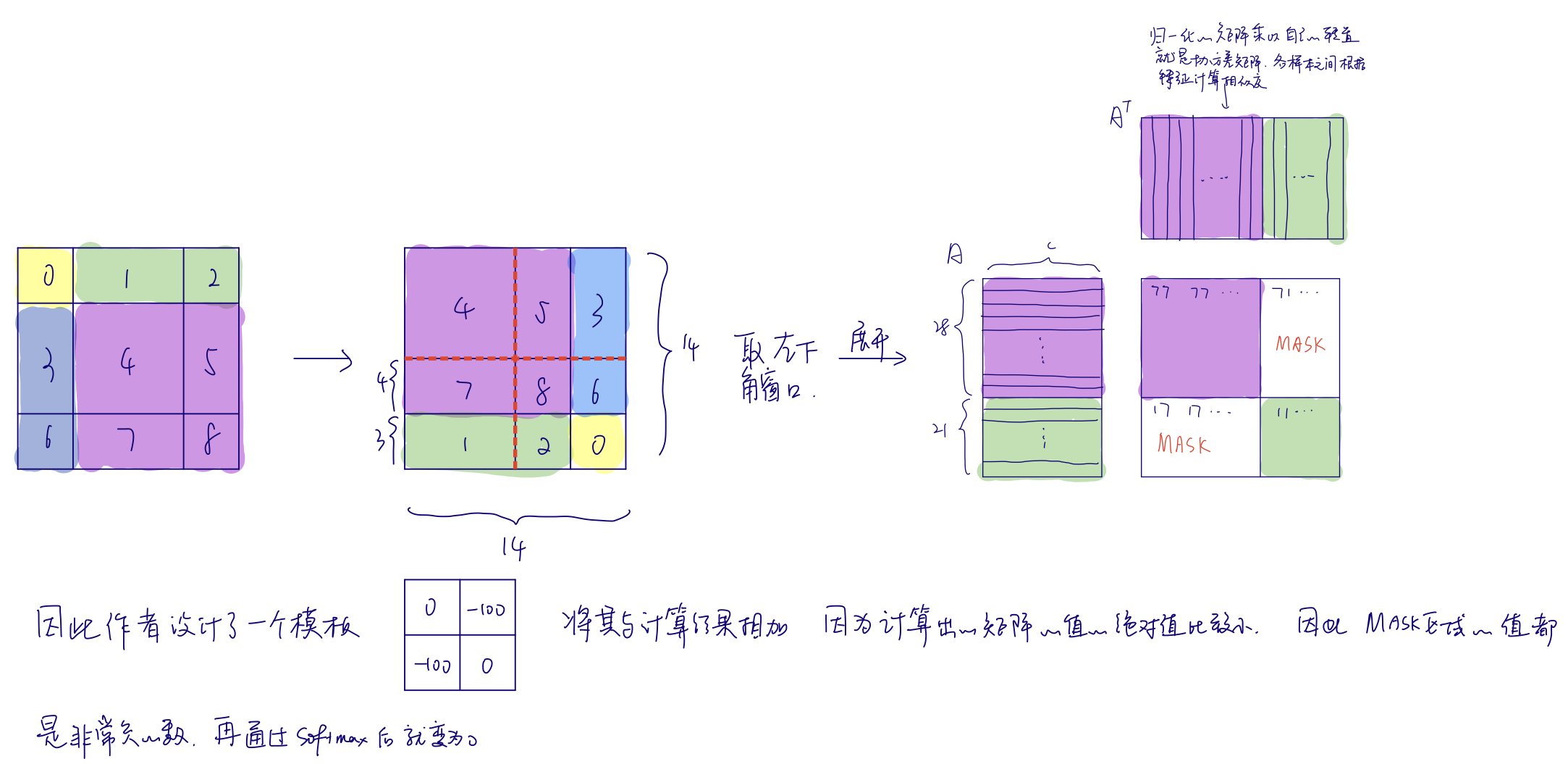
为了提高移动窗口的计算效率,作者使用了掩码,以及使用的是相对位置编码而非绝对位置编码。
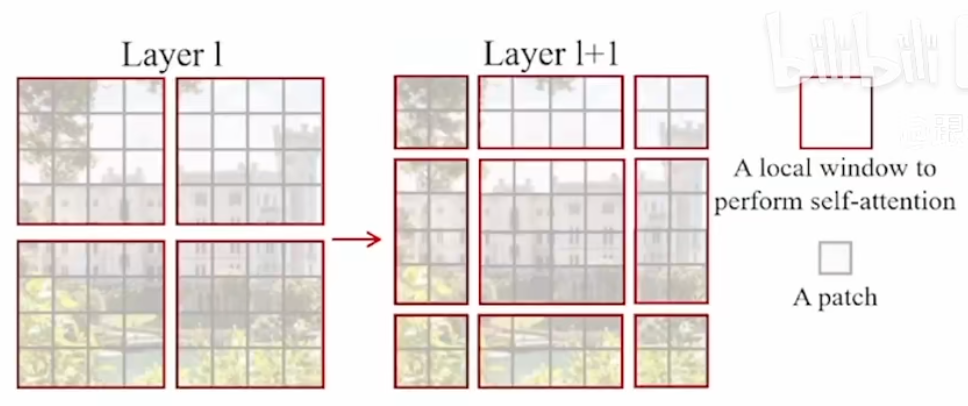
对于上图而言,虽然已经做到了窗口之间的相互通信,但经过一次移动后从四个窗口变为了九个窗口,且窗口大小不一,这样就没法把这些窗口压为一个batch直接去做自注意力了(窗口大小不一样,除了batch维没法合并)。一种解决方式是给非最大尺寸的窗口做padding,但是这样的计算量就会大大增加。因此作者提出了一种循环移位(cyclic shift)的方式:
这样窗口的数量固定了(图中为4),计算复杂度也就固定了。但是这样的话,有的窗口中的元素原本不在一起,本不应该做自注意力,这里作者提出了比较巧妙的掩码方式,参照下面的手绘图:
如果是选择右上角窗口,则展开后的样子是条纹状的。作者给出的四个窗口的掩码模版如下: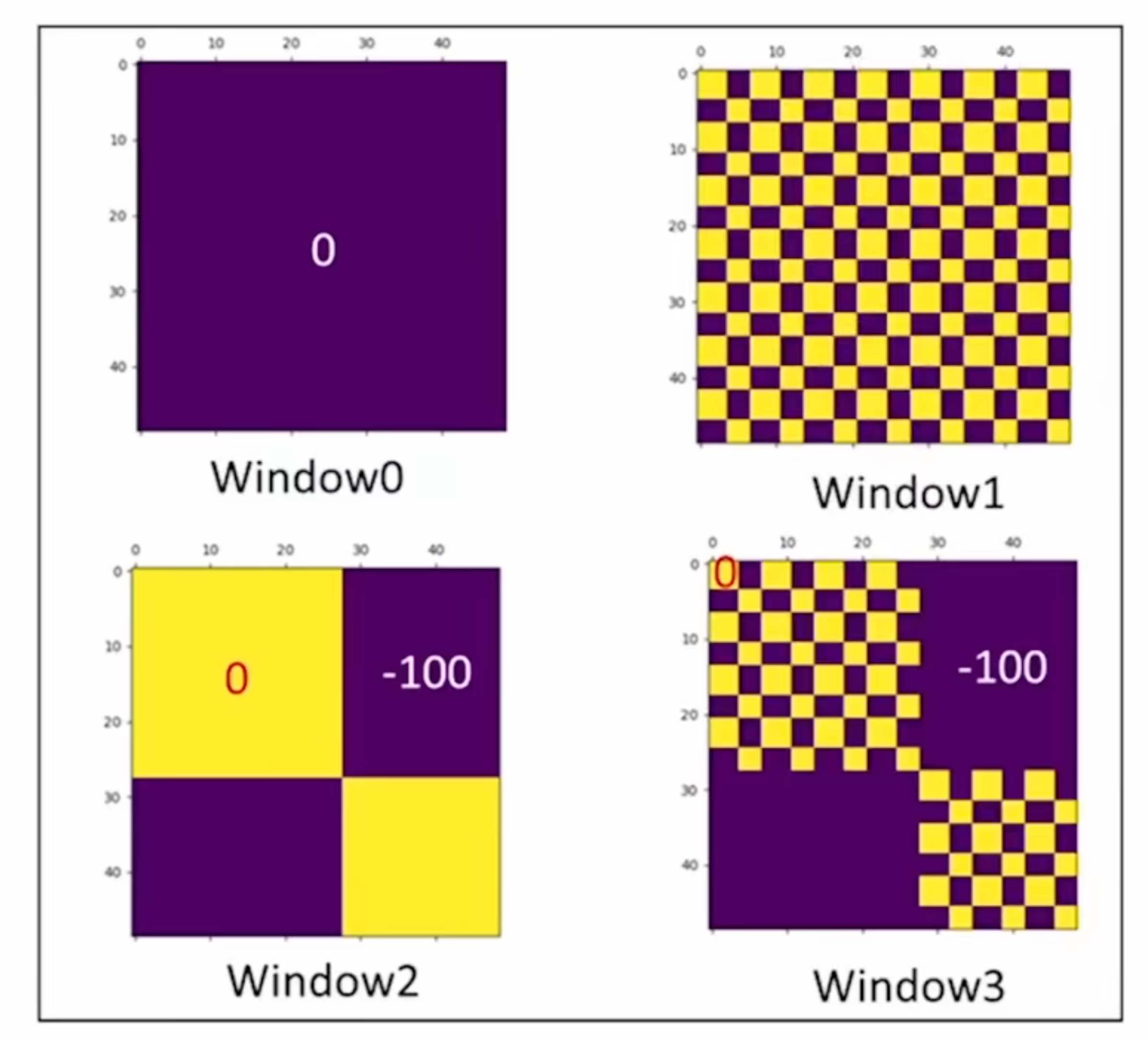
更正一下,这里用-100作为掩码值是因为自注意力值较小,这是由于LN层的作用以及比的约束例如weight decay(一般模型中间的输入输出都比较小以防止过拟合)。
计算完之后,还需要进行逆向的循环移位来还原回去(还需要保持原来图片的相对位置,不能破坏原来图像的语义信息)。
这一部分的最后,作者介绍了一下Swin Transformer的几个变体,对比了Swin Transformer全家桶与ResNet全家桶的复杂度。变量主要为向量通道维C以及每个Stage有多少个Transformer Block。
实验
作者分别使用ImageNet-1K和ImageNet-22K两个数据集做预训练,测试均在ImageNet-1K上进行(在22K数据集上预训练好的模型需要做fine tune)。
总结
~~~



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· PowerShell开发游戏 · 打蜜蜂
· 在鹅厂做java开发是什么体验
· WPF到Web的无缝过渡:英雄联盟客户端的OpenSilver迁移实战
2020-02-02 洛谷P1091合唱队形(DP)
2020-02-02 HDU1176免费馅饼(DP)
2020-02-02 HDU1029 简单DP