Codeforces Round #748 (Div. 3) E. Gardener and Tree（树的直径）
A tree is an undirected connected graph in which there are no cycles. This problem is about non-rooted trees. A leaf of a tree is a vertex that is connected to at most one vertex.
The gardener Vitaly grew a tree from 𝑛n vertices. He decided to trim the tree. To do this, he performs a number of operations. In one operation, he removes all leaves of the tree.
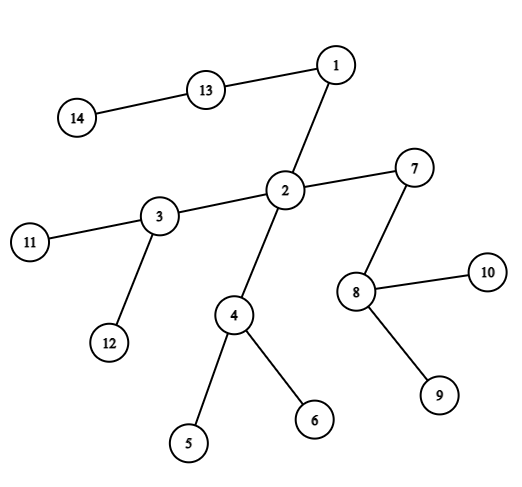Example of a tree.
For example, consider the tree shown in the figure above. The figure below shows the result of applying exactly one operation to the tree.
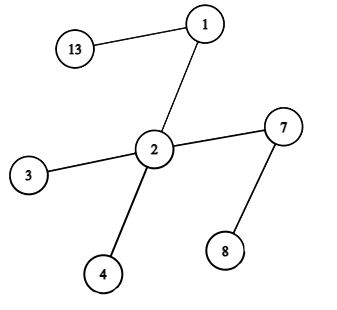The result of applying the operation "remove all leaves" to the tree.
Note the special cases of the operation:
- applying an operation to an empty tree (of 00 vertices) does not change it;
- applying an operation to a tree of one vertex removes this vertex (this vertex is treated as a leaf);
- applying an operation to a tree of two vertices removes both vertices (both vertices are treated as leaves).
Vitaly applied 𝑘k operations sequentially to the tree. How many vertices remain?
Input
The first line contains one integer 𝑡t (1≤𝑡≤1041≤t≤104) — the number of test cases. Then 𝑡t test cases follow.
Each test case is preceded by an empty line.
Each test case consists of several lines. The first line of the test case contains two integers 𝑛n and 𝑘k (1≤𝑛≤4⋅1051≤n≤4⋅105, 1≤𝑘≤2⋅1051≤k≤2⋅105) — the number of vertices in the tree and the number of operations, respectively. Then 𝑛−1n−1 lines follow, each of them contains two integers 𝑢u and 𝑣v (1≤𝑢,𝑣≤𝑛1≤u,v≤n, 𝑢≠𝑣u≠v) which describe a pair of vertices connected by an edge. It is guaranteed that the given graph is a tree and has no loops or multiple edges.
It is guaranteed that the sum of 𝑛n from all test cases does not exceed 4⋅1054⋅105.
Output
For each test case output on a separate line a single integer — the number of vertices that remain in the tree after applying 𝑘k operations.
Example
input
Copy
6
14 1
1 2
2 3
2 4
4 5
4 6
2 7
7 8
8 9
8 10
3 11
3 12
1 13
13 14
2 200000
1 2
3 2
1 2
2 3
5 1
5 1
3 2
2 1
5 4
6 2
5 1
2 5
5 6
4 2
3 4
7 1
4 3
5 1
1 3
6 1
1 7
2 1
output
Copy
7
0
0
3
1
2
大意就是给一棵无根树，每次删掉叶子结点（度为0的点），删除t轮问最后剩下几个点。
赛后裙友说可以拓扑，然而比赛的时候只会树的直径233。
一个不是很显然的做法是，首先找到树的直径，然后找到直径上中间的点（如果直径上有偶数个点的话最中间为两个点）。然后从中间的点为根进行树dp，求出来每个点到其子树的最远的叶子结点的树上距离。如果这个值大于等于k，说明这个点最后能留下来。正确性不好证明，欢迎大佬提供证明思路。
#include <bits/stdc++.h>
#define N 400005
#define ll long long
using namespace std;
int n, k, head[N], ver[2 * N], Next[2 * N], tot = 0;
void add(int x, int y) {
ver[++tot] = y, Next[tot] = head[x], head[x] = tot;
}
int d1[N], d2[N], d3[N], p, q, mx1, mx2;
void dfs1(int x, int pre, int dep) {
d1[x] = dep;
if(dep > mx1) {
mx1 = dep;
p = x;
}
for(int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if(y == pre) continue;
dfs1(y, x, dep + 1);
}
}
int pre[N];
int ans = 0;
int resi;
void dfs2(int x, int ppre, int dep) {
d2[x] = dep;
if(dep > mx2) {
mx2 = dep;
q = x;
}
for(int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if(y == ppre) continue;
pre[y] = x;
dfs2(y, x, dep + 1);
}
}
int far[N];
void dfs3(int x, int pre, int dep) {
d3[x] = dep;
bool flag = 0;
for(int i = head[x]; i; i = Next[i]) {
int y = ver[i];
if(y == pre || d3[y]) continue;
flag = 1;
dfs3(y, x, dep + 1);
far[x] = max(far[x], far[y] + 1);
}
}
int main(){
int t;
cin >> t;
while(t--) {
tot = 0;
ans = 0;
memset(head, 0, sizeof(head));
mx1 = mx2 = 0;
cin >> n >> k;
for(int i = 1; i <= n; i++) {
d1[i] = d2[i] = d3[i] = 0;
pre[i] = 0;
far[i] = 0;
}
for(int i = 1; i <= n - 1; i++) {
int x, y;
cin >> x >> y;
add(x, y);
add(y, x);
}
dfs1(1, 0, 0);
dfs2(p, 0, 0);
int len = d2[q] + 1;//直径的节点数
int root = 0, root1 = 0, root2 = 0, now = q;
if(len & 1) {
if(k >= len / 2 + 1) {
puts("0");
continue;
} else {
//找到len / 2 + 1作为根
int cnt = 1;
resi = len / 2;
while(pre[now]) {
if(cnt == len / 2 + 1) {
root = now;
break;
}
cnt++;
now = pre[now];
}
dfs3(root, 0, 1);
}
} else {
if(k >= len / 2) {
puts("0");
continue;
} else {
//找到len / 2作为根
int cnt = 1;
resi = len / 2 - 1;
while(pre[now]) {
if(cnt == len / 2) {
root1 = now;
}
if(cnt == len / 2 + 1) {
root2 = now;
}
cnt++;
now = pre[now];
}
dfs3(root1, 0, 1);
dfs3(root2, 0, 1);
}
}
//dep初始为1 能挺到
for(int i = 1; i <= n; i++) {
if(far[i] >= k) ans++;
}
cout << ans << endl;
}
return 0;
}
