Educational Codeforces Round 87 (Rated for Div. 2) C1. Simple Polygon Embedding （几何）

The statement of this problem is the same as the statement of problem C2. The only difference is that, in problem C1, nn is always even, and in C2, nn is always odd.

You are given a regular polygon with 2⋅n2⋅n vertices (it's convex and has equal sides and equal angles) and all its sides have length 11 . Let's name it as 2n2n -gon.

Your task is to find the square of the minimum size such that you can embed 2n2n -gon in the square. Embedding 2n2n -gon in the square means that you need to place 2n2n -gon in the square in such way that each point which lies inside or on a border of 2n2n -gon should also lie inside or on a border of the square.

You can rotate 2n2n -gon and/or the square.

Input

The first line contains a single integer TT (1≤T≤2001≤T≤200 ) — the number of test cases.

Next TT lines contain descriptions of test cases — one per line. Each line contains single even integer nn (2≤n≤2002≤n≤200 ). Don't forget you need to embed 2n2n -gon, not an nn -gon.

Output

Print TT real numbers — one per test case. For each test case, print the minimum length of a side of the square 2n2n -gon can be embedded in. Your answer will be considered correct if its absolute or relative error doesn't exceed 10−610−6 .

Example

Input

Copy

3
2
4
200

Output

Copy

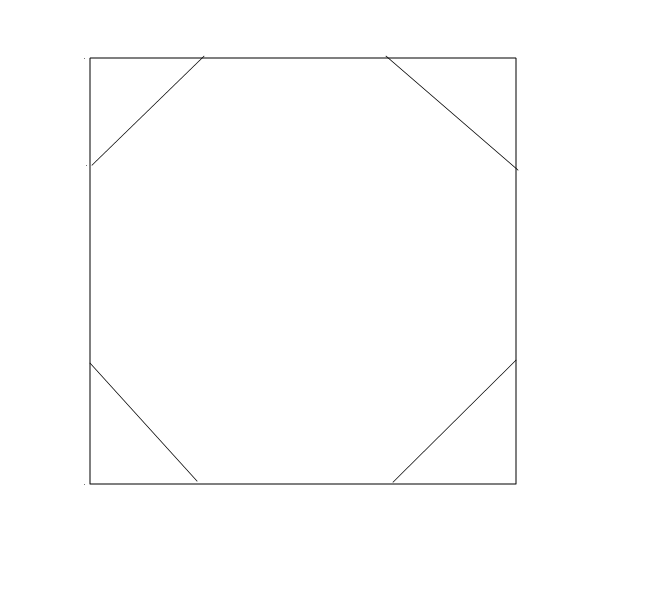
1.000000000
2.414213562
127.321336469
C1好想一点。因为n是偶数，则2*n一定是4的倍数。比如正八边形，答案要找的正方形就是类似下图这样：

正方形的每条边与多边形的其中几条边平行，而多边形的边长为1，其几何中心到每条边的距离也就能计算出了。

#include <bits/stdc++.h>
#define PI 3.1415926535898
using namespace std;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n;
        cin>>n;
        double ang=360.0/(2*n);
        ang/=2.0;
        double ans=0.0;
        ans=2*(0.5/tan(ang/180.0*PI));
        printf("%.9lf\n",ans);
     } 
}