洛谷P1364 医院设置（树形DP/二次扫描与换根法）
题目描述
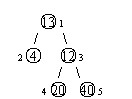
设有一棵二叉树，如图：
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 111。如上图中，若医院建在1 处，则距离和 =4+12+2×20+2×40=136=4+12+2\times20+2\times40=136=4+12+2×20+2×40=136；若医院建在 333 处，则距离和 =4×2+13+20+40=81=4\times2+13+20+40=81=4×2+13+20+40=81。
输入格式
第一行一个整数 nnn，表示树的结点数。
接下来的 nnn 行每行描述了一个结点的状况，包含三个整数 w,u,vw, u, vw,u,v，其中 www 为居民人口数，uuu 为左链接（为 000 表示无链接），vvv 为右链接（为 000 表示无链接）。
输出格式
一个整数，表示最小距离和。
输入输出样例
输入 #1
5 13 2 3 4 0 0 12 4 5 20 0 0 40 0 0
输出 #1
81
首先注意到这个题的数据范围很小，n只有1e2，因此枚举每个节点进行DFS可以通过，复杂度为O(n^2)。
考虑更高效的方法，受到题解区以及蓝书的启发，对于这种没有明显树根的题，可以采用二次扫描换根的方法，先DFS预处理，然后枚举每个点进行答案的更新。
具体来说，DFS的时候要预处理这样一个数组：size[i]代表当以1这个节点为树根时（换根），以i节点为根的子树的节点数。注意，这里的节点数实际上是子树的节点的权值和！和普通的树的重心不一样。同时，DFS时还能求出以1为树根时的距离和，存到f[1]里。
然后从1开始进行转移,设x的下一个节点是y，相较于x作为树根的路径和f[x]，可以看到f[y]的值的变化情况：
1.减少了size[y]*1，因为以y为根的子树的所有节点原来要走到x，现在可以少走一条边，总的就是减少了size[y].
2.增加了(size[1]-size[y])*1，因为除去以y为根的子树的节点，还剩下size[1]-size[y]个节点（乘上权值），而这些节点需要多走一步。
转移方程就可以写出来了f[y]=f[x]+(size[1]-size[y])*1-size[y]*1; 满足无后效性，而且能知道dp的“阶段”就是以1为树根的树的当前深度。在更新的时候对答案取min更新即可。
#include <bits/stdc++.h> #define N 105 using namespace std; int n,m,head[N],ver[2*N],Next[2*N],tot=0; int num[N],f[N],size[N],ans=0;//f[i]表示以i为根的总距离，size[i]表示以u为根的子树的大小 包括自己（对子树所有节点权值求和）。 void add(int x,int y) { ver[++tot]=y,Next[tot]=head[x],head[x]=tot; } void dfs(int x,int d,int pre) { int i; size[x]=num[x]; for(i=head[x];i;i=Next[i]) { int y=ver[i]; if(y==pre)continue; dfs(y,d+1,x); size[x]+=size[y]; } f[1]+=num[x]*(d-1);//逐层累加 注意是当前节点乘以深度减一累加上去 } void dp(int x,int pre) { int i; for(i=head[x];i;i=Next[i]) { int y=ver[i]; if(y==pre)continue; f[y]=f[x]+(size[1]-size[y])*1-size[y]*1; //转移 dp(y,x); } ans=min(ans,f[x]); } int main() { cin>>n; int i; for(i=1;i<=n;i++) { int w,u,v; scanf("%d%d%d",&w,&u,&v); num[i]=w;//节点的权值 if(u)add(i,u),add(u,i);//得存双向边 if(v)add(i,v),add(v,i); } dfs(1,1,0); ans=f[1]; dp(1,0); cout<<ans; return 0; }
