Codeforces Round #629 (Div. 3)/1328 E.Tree Queries(LCA)
You are given a rooted tree consisting of nn vertices numbered from 11 to nn . The root of the tree is a vertex number 11 .
A tree is a connected undirected graph with n−1n−1 edges.
You are given mm queries. The ii -th query consists of the set of kiki distinct vertices vi[1],vi[2],…,vi[ki]vi[1],vi[2],…,vi[ki] . Your task is to say if there is a path from the root to some vertex uu such that each of the given kk vertices is either belongs to this path or has the distance 11 to some vertex of this path.
The first line of the input contains two integers nn and mm (2≤n≤2⋅1052≤n≤2⋅105 , 1≤m≤2⋅1051≤m≤2⋅105 ) — the number of vertices in the tree and the number of queries.
Each of the next n−1n−1 lines describes an edge of the tree. Edge ii is denoted by two integers uiui and vivi , the labels of vertices it connects (1≤ui,vi≤n,ui≠vi(1≤ui,vi≤n,ui≠vi ).
It is guaranteed that the given edges form a tree.
The next mm lines describe queries. The ii -th line describes the ii -th query and starts with the integer kiki (1≤ki≤n1≤ki≤n ) — the number of vertices in the current query. Then kiki integers follow: vi[1],vi[2],…,vi[ki]vi[1],vi[2],…,vi[ki] (1≤vi[j]≤n1≤vi[j]≤n ), where vi[j]vi[j] is the jj -th vertex of the ii -th query.
It is guaranteed that all vertices in a single query are distinct.
It is guaranteed that the sum of kiki does not exceed 2⋅1052⋅105 (∑i=1mki≤2⋅105∑i=1mki≤2⋅105 ).
For each query, print the answer — "YES", if there is a path from the root to some vertex uu such that each of the given kk vertices is either belongs to this path or has the distance 11 to some vertex of this path and "NO" otherwise.
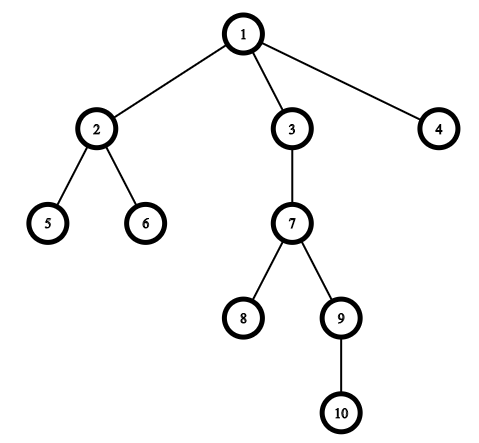
10 6 1 2 1 3 1 4 2 5 2 6 3 7 7 8 7 9 9 10 4 3 8 9 10 3 2 4 6 3 2 1 5 3 4 8 2 2 6 10 3 5 4 7
YES YES YES YES NO NO
The picture corresponding to the example:
Consider the queries.
The first query is [3,8,9,10][3,8,9,10] . The answer is "YES" as you can choose the path from the root 11 to the vertex u=10u=10 . Then vertices [3,9,10][3,9,10] belong to the path from 11 to 1010 and the vertex 88 has distance 11 to the vertex 77 which also belongs to this path.
The second query is [2,4,6][2,4,6] . The answer is "YES" as you can choose the path to the vertex u=2u=2 . Then the vertex 44 has distance 11 to the vertex 11 which belongs to this path and the vertex 66 has distance 11 to the vertex 22 which belongs to this path.
The third query is [2,1,5][2,1,5] . The answer is "YES" as you can choose the path to the vertex u=5u=5 and all vertices of the query belong to this path.
The fourth query is [4,8,2][4,8,2] . The answer is "YES" as you can choose the path to the vertex u=9u=9 so vertices 22 and 44 both have distance 11 to the vertex 11 which belongs to this path and the vertex 88 has distance 11 to the vertex 77 which belongs to this path.
The fifth and the sixth queries both have answer "NO" because you cannot choose suitable vertex uu .
以后还是该看一看E题的==
大意就是给定一棵有根树,然后给出m次询问,每次询问给出k个顶点,问能否找到一条从树根开始的路径,使得这k个顶点要么在路径上,要么到路径的距离为1.
YY的算法竟然过了...对于每次询问,首先找到这k个节点的深度最大的一个节点,然后把剩下的每个节点resi分别与这个节点deep求LCA,如果LCA就是resi的话说明resi就在树根到deep的路径上,是满足的;如果LCA不是resi的话看一下resi的深度减去LCA的深度是否等于1,如果是的话也是满足的。最后看一下如果k个节点都满足(最深的节点和自己的LCA就是自己)那么输出”YES“就可以了。
#include <bits/stdc++.h> #define N 500005 using namespace std; int n,m,s,t,tot=0,head[N],ver[2*N],Next[2*N],f[N][22],d[N],lg[500001]; int query[N]; void add(int x,int y) { ver[++tot]=y,Next[tot]=head[x],head[x]=tot; } void prework() { queue<int>q; q.push(1); d[1]=1; while(q.size()) { int x=q.front(); q.pop(); int i; for(i=head[x];i;i=Next[i]) { int y=ver[i]; if(d[y])continue; d[y]=d[x]+1; f[y][0]=x;//y节点的2^0倍祖先是x int j; for(j=1;j<=lg[d[x]];j++) { f[y][j]=f[f[y][j-1]][j-1]; } q.push(y); } } } int lca(int x,int y) { if(d[x]<d[y])swap(x,y);//使得x深度较小 int i; while(d[x] > d[y]) { x = f[x][lg[d[x]-d[y]] - 1]; } if(x==y)return x; for(i=lg[d[x]] - 1;i>=0;i--) { if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i]; } return f[x][0]; } int main() { cin>>n>>m; int i,j; memset(d,0,sizeof(d)); for(i=1;i<=n-1;i++) { int x,y; cin>>x>>y; add(x,y); add(y,x); } for(int i = 1; i <= n; ++i) lg[i] = lg[i-1] + (1 << lg[i-1] == i); prework(); for(i=1;i<=m;i++) { int k; scanf("%d",&k); int max_d=0,deep,cnt=0; for(j=1;j<=k;j++) { scanf("%d",&query[j]); if(d[query[j]]>max_d) { max_d=d[query[j]];//找到最深的节点 deep=query[j]; } } for(j=1;j<=k;j++) { int temp=lca(query[j],deep); if(d[query[j]]-d[temp]<=1)cnt++; } if(cnt==k)cout<<"YES"<<endl; else cout<<"NO"<<endl; } return 0; }




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!