Codeforces Round #629 (Div. 3) D. Carousel(思维/贪心?)
The round carousel consists of nn figures of animals. Figures are numbered from 11 to nn in order of the carousel moving. Thus, after the nn -th figure the figure with the number 11 follows. Each figure has its own type — the type of the animal corresponding to this figure (the horse, the tiger and so on). The type of animal of the ii -th figure equals titi .
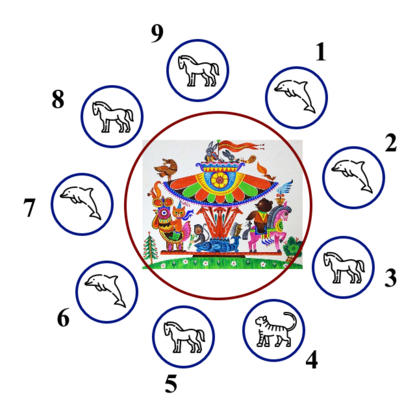 The example of the carousel for n=9n=9 and t=[5,5,1,15,1,5,5,1,1]t=[5,5,1,15,1,5,5,1,1] .
The example of the carousel for n=9n=9 and t=[5,5,1,15,1,5,5,1,1]t=[5,5,1,15,1,5,5,1,1] . You want to color each figure in one of the colors. You think that it's boring if the carousel contains two different figures (with the distinct types of animals) going one right after another and colored in the same color.
Your task is to color the figures in such a way that the number of distinct colors used is the minimum possible and there are no figures of the different types going one right after another and colored in the same color. If you use exactly kk distinct colors, then the colors of figures should be denoted with integers from 11 to kk .
The input contains one or more test cases.
The first line contains one integer qq (1≤q≤1041≤q≤104 ) — the number of test cases in the test. Then qq test cases follow. One test case is given on two lines.
The first line of the test case contains one integer nn (3≤n≤2⋅1053≤n≤2⋅105 ) — the number of figures in the carousel. Figures are numbered from 11 to nn in order of carousel moving. Assume that after the nn -th figure the figure 11 goes.
The second line of the test case contains nn integers t1,t2,…,tnt1,t2,…,tn (1≤ti≤2⋅1051≤ti≤2⋅105 ), where titi is the type of the animal of the ii -th figure.
The sum of nn over all test cases does not exceed 2⋅1052⋅105 .
Print qq answers, for each test case print two lines.
In the first line print one integer kk — the minimum possible number of distinct colors of figures.
In the second line print nn integers c1,c2,…,cnc1,c2,…,cn (1≤ci≤k1≤ci≤k ), where cici is the color of the ii -th figure. If there are several answers, you can print any.
4 5 1 2 1 2 2 6 1 2 2 1 2 2 5 1 2 1 2 3 3 10 10 10
2 1 2 1 2 2 2 2 1 2 1 2 1 3 2 3 2 3 1 1 1 1 1
给动物涂色,唯一的限制是相邻的不同种动物不能为同一种颜色(注意这是一个环),求最少需要的颜色以及涂色方案。
首先可以看出来只用一种颜色的话肯定必须要所有动物都是同一种。其次考虑只用两种颜色,一开始我想的是直接1 2 1 2 ...这样涂,但是如果总数为奇数且1和n非同种动物的话处理起来其实也比较麻烦....后来参考别人的博客,发现可以在同类相邻动物涂成一种颜色的前提下1 2 1 2这样涂,这样的话如果1和n是同种动物或1和n不同类且涂的颜色也不同时肯定是合法的;对于不合法的情况,首先找到任意一处连续的动物,从这段中间开始把后面全换成相反的颜色(这样能保证颜色不增加且合法,很巧妙),如果没有连续段的话就只能把最后一个数涂成3了。
#include <bits/stdc++.h> using namespace std; int num[200005],color[200005]; int main() { int t; cin>>t; while(t--) { int n; cin>>n; int i; int k=1; bool same=1;//判断是否全为一个数 int conti=0;//判断是否有连续区域,有的话设置为下标 scanf("%d",&num[1]); for(i=2;i<=n;i++) { scanf("%d",&num[i]); if(num[i]!=num[i-1])same=0; if(num[i]==num[i-1])conti=i; } if(same) { cout<<1<<endl; for(i=1;i<=n;i++)printf("1 "); cout<<endl; } else { color[1]=1; for(i=2;i<=n;i++) { if(num[i]==num[i-1])color[i]=color[i-1]; else color[i]=3-color[i-1]; } if(num[1]==num[n]||num[1]!=num[n]&&color[1]!=color[n]) { cout<<2<<endl; for(i=1;i<=n;i++)printf("%d ",color[i]); cout<<endl; } else { if(conti) { cout<<2<<endl; for(i=1;i<=n;i++) { if(i<conti) printf("%d ",color[i]); else printf("%d ",3-color[i]); } cout<<endl; } else { color[n]=3; cout<<3<<endl; for(i=1;i<=n;i++)printf("%d ",color[i]); cout<<endl; } } } } }
CF上最少xx这种有的时候根据样例直接考虑一下0 1 2 3这些比较小的数,极有可能是思维题。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!