Codeforces 149D. Coloring Brackets（区间DP+记忆化搜索）

Once Petya read a problem about a bracket sequence. He gave it much thought but didn't find a solution. Today you will face it.

You are given string s. It represents a correct bracket sequence. A correct bracket sequence is the sequence of opening ("(") and closing (")") brackets, such that it is possible to obtain a correct mathematical expression from it, inserting numbers and operators between the brackets. For example, such sequences as "(())()" and "()" are correct bracket sequences and such sequences as ")()" and "(()" are not.

In a correct bracket sequence each bracket corresponds to the matching bracket (an opening bracket corresponds to the matching closing bracket and vice versa). For example, in a bracket sequence shown of the figure below, the third bracket corresponds to the matching sixth one and the fifth bracket corresponds to the fourth one.

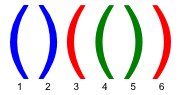
You are allowed to color some brackets in the bracket sequence so as all three conditions are fulfilled:

• Each bracket is either not colored any color, or is colored red, or is colored blue.
• For any pair of matching brackets exactly one of them is colored. In other words, for any bracket the following is true: either it or the matching bracket that corresponds to it is colored.
• No two neighboring colored brackets have the same color.

Find the number of different ways to color the bracket sequence. The ways should meet the above-given conditions. Two ways of coloring are considered different if they differ in the color of at least one bracket. As the result can be quite large, print it modulo 1000000007 (10⁹ + 7).

Input

The first line contains the single string s (2 ≤ |s| ≤ 700) which represents a correct bracket sequence.

Output

Print the only number — the number of ways to color the bracket sequence that meet the above given conditions modulo 1000000007 (10⁹ + 7).

Examples

Input

Copy

(())

Output

Copy

12

Input

Copy

(()())

Output

Copy

40

Input

Copy

()

Output

Copy

4
又是一道不看题解打死也想不到的好题...题意很简单，给定一个合法的括号序列要求给一些括号染色，问染色后最多有多少种不同的括号序列。染色规则有三条：1.可以染红/蓝或者不染色。2.每一对匹配的括号有一个必须染色，另一个必须不染色。3.相邻的括号不能同色（但可以都不染色）。
给了我区间DP的标签一开始也毫无思路。首先就是应该想到要开四维数组，这样既能记录区间的左右端点位置也能记录左右端点染什么色。然后根据题意，需要我们知道哪个括号和哪个括号配对，这需要用到栈来记录。其次就是记忆化搜索，为什么要用记忆化搜索而不是常规的区间DP更新呢？大佬曰：
本题要求配对的括号有且只有一个染色，但按一般的方式难以保证配对的括号在同一区间内，即不能保证转移中用到的序列都是合法的，处理比较麻烦。而采用记忆化搜索的方式，所有操作都是在原来的合法序列上增加/删除一对括号，或是将合法序列分割成两个合法序列/将两个合法序列合并，得到的仍然是合法序列，处理起来就方便得多；而且还不需要考虑不合法的状态，时间上也得到优化。我的理解是因为给的括号序列是有序的，且每个括号一一配对，搜索的话不会破坏括号序列的合法性。然后分三类情况进行转移。
参考博客：https://blog.csdn.net/hhz6830975/article/details/79436315?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
https://blog.csdn.net/weixin_30404405/article/details/95101209?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

#include <bits/stdc++.h>
#define MOD 1000000007
using namespace std;
char s[705];
long long dp[705][705][3][3]={0};//前两维表示l~r区间，后两维分别表示左括号和右括号的颜色 0无色，1红色，2蓝色 
int match[705];
void dfs(int l,int r)//注意 因为输入括号序列一定是合法的，所以一定不会出现左端点是)而右端点是(之类的情况 
{
    int i,j,p,q;
    if(r==l+1)//长度为2的区间 由于记忆化搜索 所以这里长度为2的区间一定是匹配的 
    {
        dp[l][r][0][1]=dp[l][r][1][0]=dp[l][r][0][2]=dp[l][r][2][0]=1;
        return;
    }
    else if(match[l]==r)
    {
        dfs(l+1,r-1);//先搜索再更新dp数组 有点类似...线段树的上传？ 
        for(i=0;i<=2;i++)
        {
            for(j=0;j<=2;j++)
            {
                if(j!=1) dp[l][r][0][1]=(dp[l][r][0][1]+dp[l+1][r-1][i][j])%MOD;//这里的j！=1是为了保证不会有相邻位置的颜色一样 其他同理 
                if(j!=2) dp[l][r][0][2]=(dp[l][r][0][2]+dp[l+1][r-1][i][j])%MOD;
                if(i!=1) dp[l][r][1][0]=(dp[l][r][1][0]+dp[l+1][r-1][i][j])%MOD;
                if(i!=2) dp[l][r][2][0]=(dp[l][r][2][0]+dp[l+1][r-1][i][j])%MOD;
              } 
        }
    }
    else//不匹配的话 一定是(...)(...) eg：()()()因为搜索时不会出现整个区间不匹配的情况比如))( 而长度为2的区间在之前的情况里 
    {
        dfs(l,match[l]);
        dfs(match[l]+1,r); 
        for(i=0;i<=2;i++)
        {
            for(j=0;j<=2;j++)
            {
                for(p=0;p<=2;p++)
                {
                    for(q=0;q<=2;q++)
                    {
                        if((p==1&&q==1)||(p==2&&q==2))continue;//不能仅为i==p 因为相邻都为0是可以的 
                        dp[l][r][i][j]=(dp[l][r][i][j]+(dp[l][match[l]][i][p]%MOD*dp[match[l]+1][r][q][j]%MOD)%MOD)%MOD;//类似排列组合 把方案数相乘 因为dp数组已经具体到颜色了 所以直接相乘就好不会有矛盾 //注意这里并不是找决策点，而是累加数目 
                    }//记得边模边乘 
                }
            }
        }
     } 
}
int main()
{
    cin>>s;
    memset(dp,0,sizeof(dp));
    int i,j;
    stack<int>stk; 
    for(i=0;i<strlen(s);i++)//每一个左右括号都偶是唯一匹配的 用传统的栈确定左右括号匹配的编号 
    {
        if(s[i]=='(')stk.push(i);
        else
        {
            int temp=stk.top();
            match[temp]=i;
            match[i]=temp;
            stk.pop();
        }
    } 
    dfs(0,strlen(s)-1);
    long long ans=0;
    for(i=0;i<=2;i++)
    {
        for(j=0;j<=2;j++)
        {
            ans=(ans+dp[0][strlen(s)-1][i][j])%MOD;//l~r区间的所有可能情况累加 
        }
    }
    cout<<ans;
    return 0;
}