初探深度学习
深度学习
特征提取、物体检测、语义标注、实体标注、描述生成、多媒体问答、多媒体叙事
深度学习的”不能“
-
算法输出不稳定,容易被”攻击“
比如在一个图片中改变一个像素值,就可能导致识别天差地别。
-
模型复杂度高,难以纠错和调试
(李世石和alphogo)
-
模型层级复合程度高,参数不透明
-
端到端训练方式对数据依赖性强,模型增量性差
当样本数据量小的时候,深度学习无法体现强大的拟合能力
深度学习没有迁移能力,把许多相关联的东西混合在一起无法识别。
-
专注直观感知类问题,对开放性推理能力无能为力
-
人类知识无法有效引入监督,及其偏见难以避免
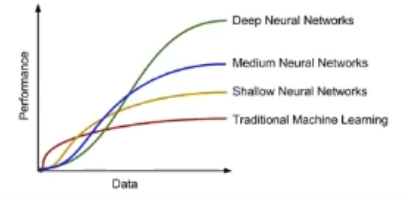
神经元
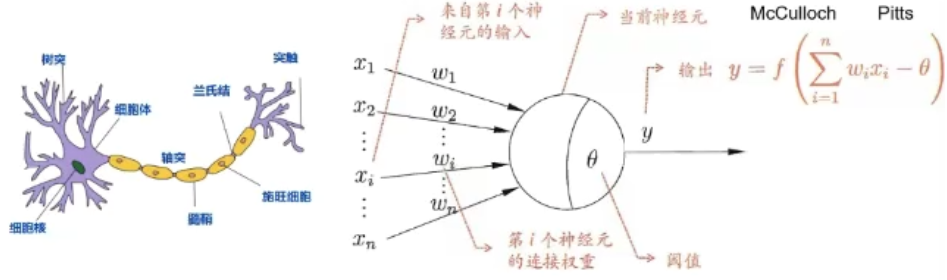
| 生物神经元 | M-P神经元 |
|---|---|
| 多输入单输出 | 多输入信号进行累加\(\sum \limits_i x_i\) |
| 空间整合 | 同上 |
| 兴奋性/抑制性输入 | 权值\(w_i\)正负模拟兴奋\抑制,大小模拟强度 |
| 阈值特性 | 输入和超过阈值θ |
激活函数
激活函数f,神经元继续传递信息,产生新连接的概率(超过阈值被激活但不一定会传递)
没有激活函数相当于矩阵相乘(1. 多层和一层一样 2.只能拟合线性函数)
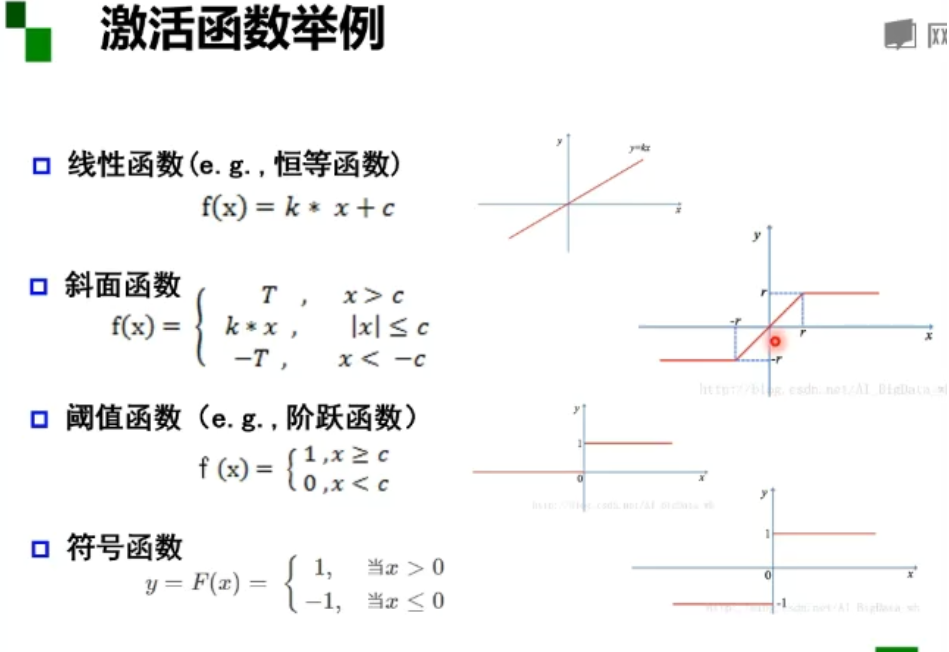
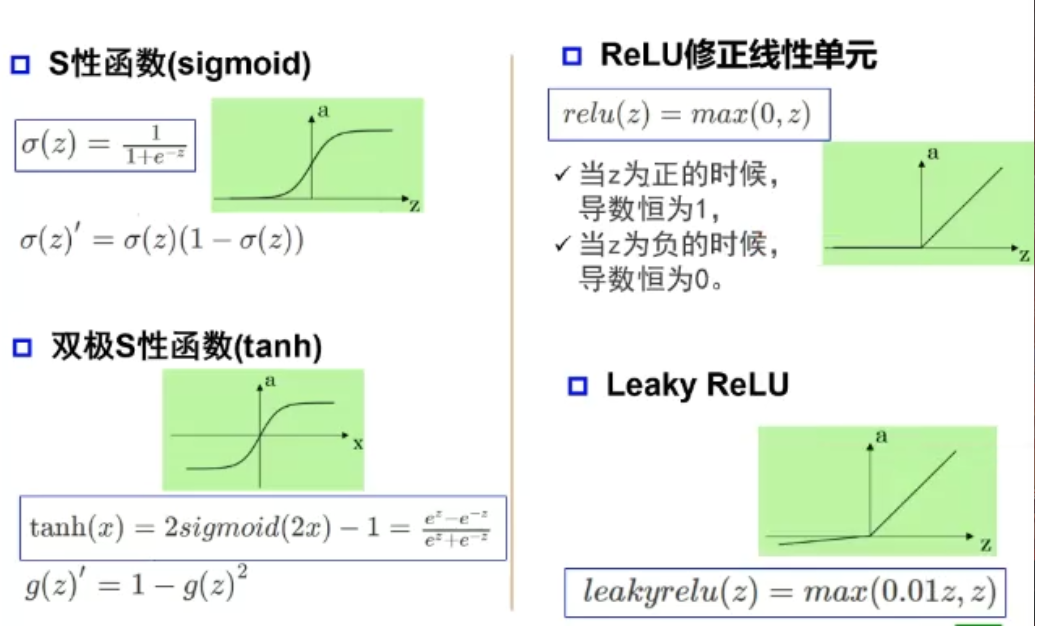
M-P神经元的权重是预先设置好的,无法学习
单层感知器是首个可以学习的人工神经网络
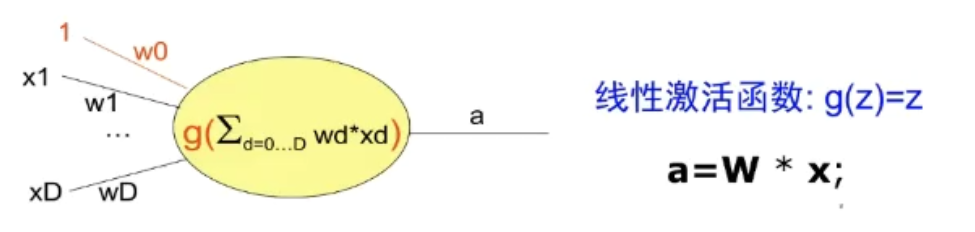
单层感知器
非线性激活函数 0 和 1 与或非
多层感知器
三层感知器实现同或门
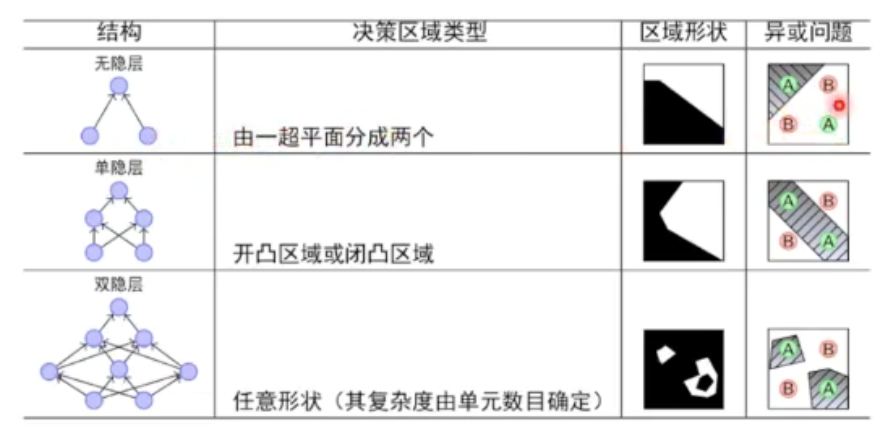
万有逼近定理
如果一个隐层包含足够多的神经元,三层前馈神经网络(输入-隐层-输出)能以任意精度逼近任意预定的连续函数
当隐层足够宽时,双隐层感知器(输入-隐层1-隐层2-输出)可以逼近任意非连续函数,解决任何复杂的分类问题。
神经网络每一层的作用
每一层数学公式\(\vec y=a(W · \vec x + b)\)
完成输入->输出空间变换
| 作用 | 公式参数 |
|---|---|
| 升/降维 | W·x |
| 放大/缩小 | W·x |
| 旋转 | W·x |
| 平移 | +b |
| 弯曲 | a(·) |
神经网络学习如何利用矩阵的线性变换加激活函数的非线性变换,将原始输入空间投影到线性可分的空间去分类/回归。
增加节点数:增加维度,即增加线性转换能力
增加层数:增加激活函数的次数即增加非线性转换次数
在神经元总数相当的情况下,增加网络深度可以比增加宽度带来更强的网络表示能力,产生更多的线性区域。
深度和宽度对函数复杂度的贡献是不同的,深度的共享是指数增长的,而宽度的贡献是线性的。
误差反向传播
多层神经网络可以看成一个复合的非线性多元函数(逐层传递)
希望损失\(\sum (F(x^i),y^i)\)最小
梯度是什么?
多元函数f(x,y)在每个点有多个方向,每个方向都可以计算导数,称为方向导数。
梯度是一个向量:
- 方向是最大方向导数的方向
- 模为方向导数的最大值
无约束优化:梯度下降
参数沿负梯度方向更新可以使函数值下降。
残差:损失函数在某个结点的偏导
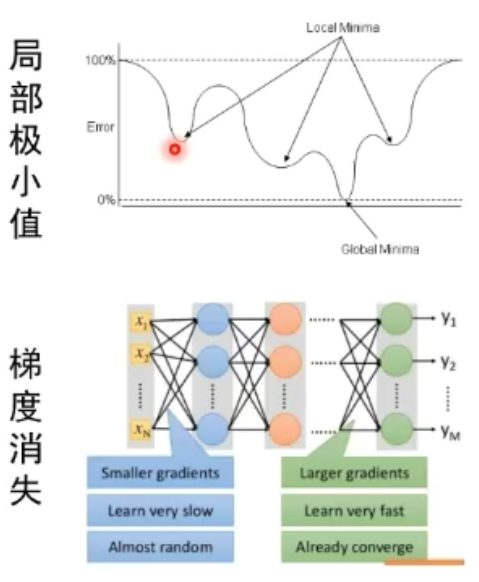
深层神经网络的问题:梯度消失
激活函数的梯度容易落到饱和区,逐层相乘后使损失无法继续传播。
为什么加入多个隐层的效果不如一个隐层?
在前向输入中最后一层接受的输入要经过没有更新的前几层的输入,使得最后接收的是混乱的输入。
增加深度会造成梯度消失,误差无法传播,同时多层网络容易陷入局部极值,难以训练。
所以三层神经网络是主流。(层数控制要少)
深度学习
逐层预训练
之前方法的缺点
每次训练三层的网络,然后把中间得到的表示累加到最后的网络中,然后逐层累加。
受限玻尔兹曼机和自编码器
自编码器
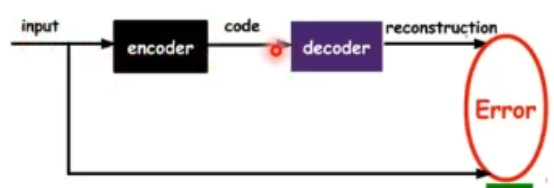
自编码器假设 输出与输入相同,是一种尽可能复现输入信号的神经网络
将input输入一个encoder编码器,就会得到一个code;加一个decoder解码器输出信息。
通过调整encoder和decoder的参数,使得重构误差最小
没有额外监督信息,无标签数据,误差的来源是直接重构后的信号与原输入相比得到。
自编码器一般是一个多层神经网络(最简单:三层)
训练目标是使输出层与输入层误差最小;
中间隐层代表输入的特征,可以最大程度上代表原输入信号
自编码器的学习目标是最小化重构错误!
自编码器是一种网络结构,可配合其他结构搭建深度网络(卷积,池化)
受限玻尔兹曼机RBM
受限玻尔兹曼机是两层神经网络,包含可见层v(输入层)和隐藏层h,不同层之间全连接,层内无连接->二分图。
与感知器不同,受限玻尔兹曼机没有显示重构过程:
输入v,通过p(h|v)得到隐藏层h;输入h,通过p(v|h)得到v
目的是让隐藏层得到的可见层v'与原来的可见层v分布一致,从而使隐藏层作为可见层输入的
特征
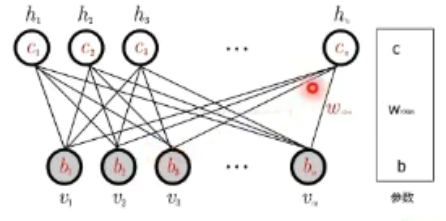
两个方向权值w共享,偏置不同
模型参数:w,c,b
条件概率建模:
联合概率->条件概率
假设是标准玻尔兹曼分布:所有节点是二进制变量(0,1)
模型求解:
优化目标:网络表示的概率分布与输入样本分布尽可能的接近
可见层v的似然:
梯度下降->基于Gibbs采样的对比散度:
状态组合数目太多,难以直接求和->采样来近似计算
深度信念网络(DBN)
一个DBN模型由若干个RBM堆叠而成,最后加一个监督层。
| 比较 | 自编码器 | 受限玻尔兹曼机 |
|---|---|---|
| 结构上 | 编码和解码函数不同:W1,W2 | 共享权重矩阵W,两个偏置向量 |
| 原理上 | 非线性变换学习特征,是确定的,特征值可以为任何实数 | 基于概率分布定义,高层表示为底层特征的条件概率,输出只有两种状态(未激活/激活),用二进制(0/1)b表示 |
| 训练优化 | 通过损失函数L最小化重构输入数据,直接用BP优化求解 | 基于最大似然,能量函数偏导无法直接计算,采用采样方法进行估计 |
| 生成/判别模型 | 对联合概率密度建模,是生成式模型 | 直接对条件概率建模,是判别式模型 |


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步