Bundle Adjustment
Bundle Adjustment
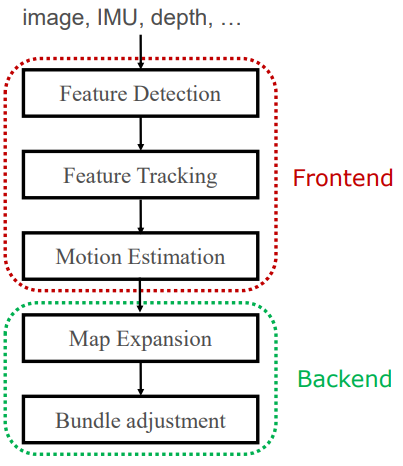
BA是SFM和SLAM中非常重要的环节。

以SLAM为例,看一下BA的作用。
SLAM从二维图像的运动中推测相机的三维运动。通常用特征点表征图像的运动,用BA来恢复每个特征点在三维的位置以及每一帧图像的三维运动。
基础理论
相机参数\(C_1,...,C_{N_c}\),三维点\(X_1,...X_{N_p}\),\(\pi(C_i,X_j)\)是把每个三维点投影到图像上,\(x_{ij}\)是图像上对应的特征点。
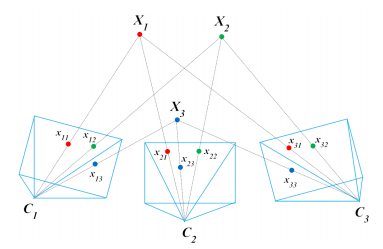
恢复的相机运动和三维点,把三维点通过相机的运动参数投影到图像上与图像上提取的特征点的距离——重投影误差。
把每一个点都投影到图像上与对应的特征点保持一致的话,是最优的。
难点:投影方程是非线性的——\(\pi(C_i,X_j)\)
这个问题就称为非线性的最小二乘,那么非线性的最小二乘怎么求解呢?
如果方程是线性的,那么就是线性的最小二乘,解起来比较简单。
如果方程是非线性的
其中\(\hat{x}\)是当前的解,可以随便给初值。假设给的初值比最优解差一个\(\delta_x\)。将\(x^*\)代入能量函数中
把能量函数在最优处的方程做一个一阶的线性展开,在\(\hat{x}\)的状态下做展开
这里\(J\)是雅各比矩阵:
从而能量函数可以写成线性的形式:
假设最优值 = 初值+\(\delta_x\),上式解出\(\delta_x\)后带入式子,得到新的变量\(\hat{x}\),重复展开,解下一次迭代的\(\delta_x\),不断的进行逼近最优解。
概念:
-
Hessian matrix
\(A^TA\) 和 \(J^TJ\)
-
normal equation
\(A^TAx=-A^Tb\) 和 \(J^TJ\delta_x =-J^T\epsilon\)
BA的难点(和其他的非线性最小二乘的区别):

BA的重投影方程很特殊,每一个重投影方程只 会关联到一个camera和一个point,所以Hessian matrix非常稀疏。

最大的区别就在于,显式地利用了Hessian matrix的稀疏性,使得优化的效率大幅度提升。
一个简单的例子:
- 3个摄像机
- 4个点
- 每一个点在所有的摄像机里都可见
其雅各比矩阵J的形式为:

做一些简单的线性代数的运算:
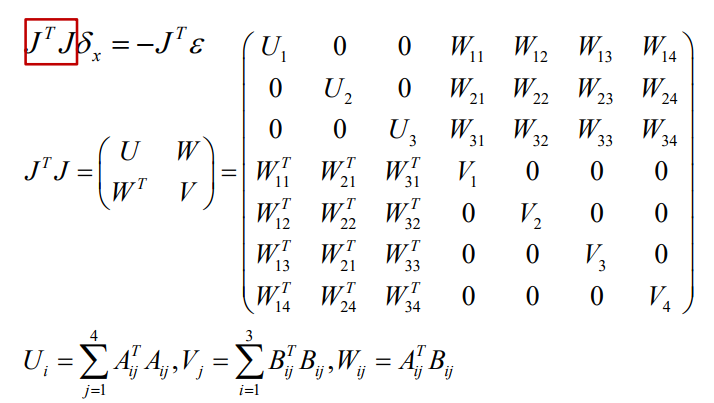
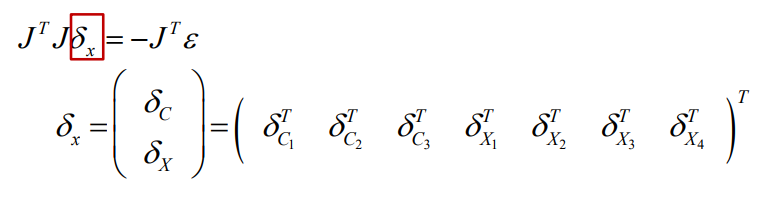
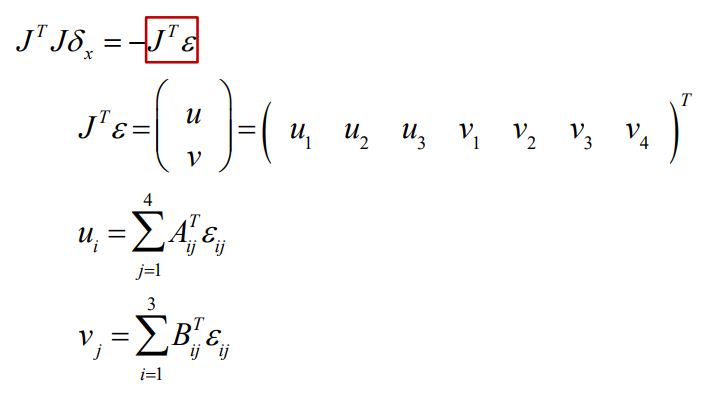
在实际的情况下,不是所有的点都在所有的摄像机里都可见,因此\(J\)变得更加稀疏。
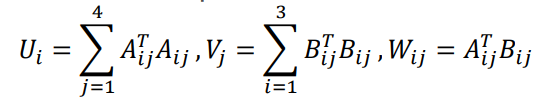
如果第j个点在第i个摄像机里不可见,则\(A_{ij} = B_{ij} = 0\)
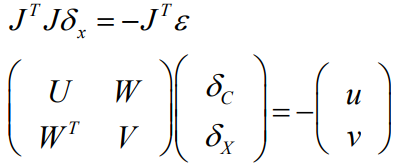
对方程进行高斯消元,左右同时乘高斯消元的稀疏矩阵,能让右上角的分量变成0。

通常来说,三维点个数远大于相机的个数,消元后,只需要\(S\delta_c = -(u-WV^{-1}v)\)即可求解摄像机 \(\delta_C\),所以问题被简化了。
把解出的\(\delta_C\)带回,用第二个式子即可求解点\(\delta_X\)。
最麻烦的是求解\(S = U - WV^{-1}W^{-T}\)
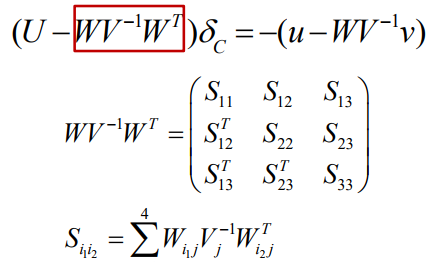
\(S_{i_1i_2}\)是两个相机之间的分量。把两个相机之间所有可见的点加起来。
在实际的情况下,不是所有的点都在所有的摄像机里都可见,因此
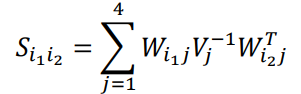
如果第\(i_1\)个相机与第\(i_2\)个相机没有公共点, 则\(S_{i_1i_2} = 0\)
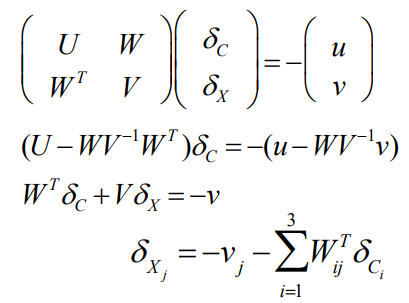
每个点都可以被单独的求解
如果第\(j\)个点在第\(i\)个相机中观察不到,则\(W_{ij} = 0\)
总结:
-
构建normal equation

-
构建Schur complement

-
解决相机问题
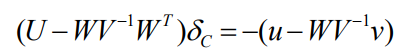
- Sparse Cholesky factorization
- Preconditioned Conjugate Gradient(PCG)
核函数
在前面的BA问题中,将最小化误差项的二范数平方和作为目标函数,这种做法存在一个严重的问题:
如果出于误匹配等问题,某个误差项给的数据是错误的,即把一条原本不应该加到图中的边给加进去了,然而优化算法并不能辨别出这个错误数据,它会把所有的数据都当作误差来处理。在算法看来,这相当于我们突然观测到了一次不可能产生的数据,在图优化中会有一条误差很大的边,梯度也很大,意味着调整与它相关的变量会使目标函数下降很多。
所以算法将试图优先调整这条边所连接的节点的估计值,使它们顺应这条边的无理要求,由于这条边的误差真的很大,往往会抹平其他正确的边的影响,使得优化算法专注于调整一个错误的值。
原因是,误差很大时,二范数增长的太快。于是就有了核函数的存在。核函数保证每条边的误差不会太大导致掩盖其他的边。
具体方式是,把原先误差的二范数度量替换成一个增长没那么快的函数,同时保证自己的光滑性质(不然无法求导)。
因为它们使得整个优化结果更为稳健,所以又叫它们鲁棒核函数。
常用的Huber核:
当误差e大于某个阈值\(\delta\)后,函数增长由二次形式变成了一次形式,相当于限制了梯度的最大值。同时Huber核函数又是光滑的,可以很方便的求导。
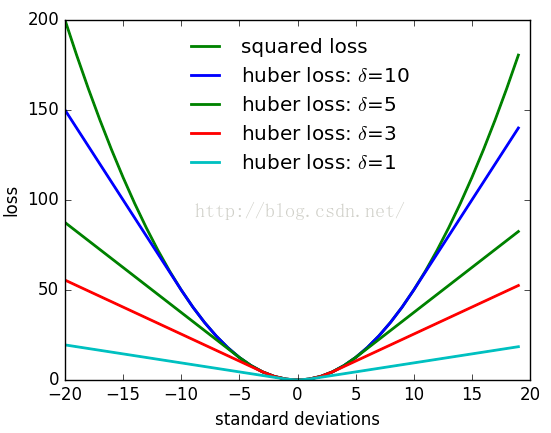
测试:
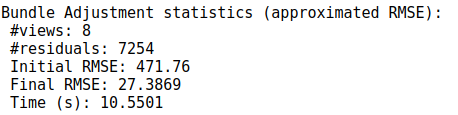
同样使用8张图片进行SFM的BA优化,每张图使用ORB特征提取2000个关键点,以下为最终测试结果。
Huber(4):
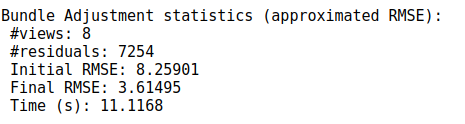
Huber(1):
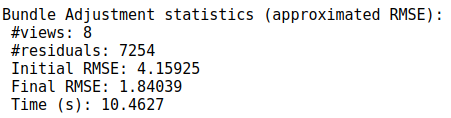
没有核函数: