HSfM Hybrid Structure-from-Motion《学习笔记》

HSfM: Hybrid Structure-from-Motion

Abstract

为了估计初始的相机位姿，SFM方法可以被概括为增量式或全局式。

虽然增量系统在鲁棒性和准确性方面都有所进步，在效率上仍是其主要的挑战。

为了解决这个问题，全局重建系统通过对极几何图中同时估计所有相机的位姿，但它对外点很敏感。在这个工作里，我们提出了一个混合式sfm方法在统一的框架下解决效率，准确性和鲁棒性的问题。

进一步来说，我们提出一种社区化的自适应的平均方法，首先以全局方式估计相机旋转，然后基于这些估计的摄像机旋转，以增量式的方法去计算相机中心。

大量的实验表明，在计算效率方面，我们的混合方法的执行效果与许多最新的全局SfM方法相似或更好，同时与其他两种最新的状态相比，实现了相似的重构精度和鲁棒性渐进的SfM方法。

Introduction

SFM技术是指通过一系列图片估计三维场景结构和相机位姿。它通常包含三个模块，特征提取和匹配，初始相机位姿估计和BA。根据初始相机姿势的估算方式不同，sfm可以被笼统的分为两类：增量式和全局式。

对于增量式方法，一种方法是选择一些种子图像进行初始重建，然后重复添加新图像。另一种方法是首先将图像聚集成原子模型，然后重建每个原子模型，然后逐步合并它们。

可以说，增量方式是3D重建最流行的策略。然而，这种方法对初始种子模型重建和模型生成方式很敏感。

另外，重建误差随着迭代的进行而累积。对于大规模的场景重建，重建的结构可能会发生场景漂移。

此外，反复执行耗时的捆绑调整BA，这大大降低了系统的稳定性和效率。

为了解决这些不足，全局sfm方法在近些年变得更加流行。

对于全局式方法，初始相机的位姿同时从对极几何图像（EG）估计，图的顶点对应图像，边链接匹配的图像对，BA只执行一次，这在系统效率和可扩展性方面带来了更大的潜力。

全局摄像机位姿估计的通用pipeline包括两个步骤：旋转平均和位移平均。

对于旋转平均，它的准确性主要依赖于两个因素：EG的结构和成对对极几何的准确性。目前许多文献仅使对极边缘的残差最小化。作为结果，当摄像机分布不佳时，例如Internet数据这些方法有时候效果并不好。

对于位移平均，由于对极几何仅编码成对平移的方向（缺少尺度），对于计算相机位置是很困难的。此外，位移估计对特征匹配的外点更加敏感。相比之下，增量式sfm受益于RANSAC方法，可以消除不良的几何形状。

因此，我们期望使用增量式和全局式两者方法的优点。

Contribution

1. 我们提出了一种新的混合SfM方法，以在统一框架中解决效率，鲁棒性和准确性问题。
2. 提出了一种基于社区的旋转平均方法，该方法同时考虑了EG的结构和成对几何的准确性。
3. 基于估计的摄像机旋转量，以增量方式估计摄像机中心。对于每次添加的摄像机，摄像机旋转和固有参数均保持不变，而摄像机中心和场景结构则通过修改后的束调整进行调整。

在我们的hybrid SFM，全局平均旋转降低了场景漂移的风险以及增量中心估计可提高对嘈杂数据的鲁棒性。在已知摄像机旋转的情况下，仅需两个场景点即可完成摄像机中心注册。因此RANSAC方法使我们的方法对异常值十分鲁棒。并且在每个摄像机添加的步骤中可以校准更多摄像机。另外，由于在添加的每个摄像机中场景结构和摄像机中心都得到了改进，因此我们的混合工作中的BA比传统摄像机快的多。

在实验中，我们评估了混合SfM系统在连续和无序图像数据。就重构摄像机的数量而言，我们的方法优于许多最新的全局SfM方法，这表明我们的方法对外点更鲁棒。

在重建效率方面，我们的方法的性能与全局SfM方法相似或更好，但其速度比Bundler的并行版本快13倍，比Theia的并行版本快5倍。

Related Work

增量式SFM

一种重建场景的方法是从二或三张种子视图开始，然后逐步将新视图添加到系统中以初始化最终BA。这样的方法对种子选择标准很敏感，并且累积的错误可能会导致场景漂移。 为了降低累积错误，VSFM和COLMAP都建议在图像添加过程中重新划分轨迹。

另一种方法是先创建原子3D模型，然后合并不同的模型。这种分层方法对原子模型的选择和模型的增长方案很敏感。

对于大型图像集合，由于重复激活BA，所有增量方法都会遇到场景漂移和繁重的计算负荷的情况。

全局式SFM

全局式SFM方法同时估计所有相机的位姿，只使用BA一次。相机位姿估计过程主要包括两个部分：旋转平均和位移平均。

旋转平均：

旋转平均可以同时从成对的相对旋转估计所有摄像机旋转，这在许多文献中都得到了很好的研究。

• A. Chatterjee and V. M. Govindu. Efficient and robust large- scale rotation averaging. In ICCV, pages 521–528. IEEE, 2013.
• V. M. Govindu. Lie-algebraic averaging for globally consis- tent motion estimation. In CVPR, pages 1–8. IEEE, 2004.
• R. Hartley, J. Trumpf, Y. Dai, and H. Li. Rotation averaging. International Journal of Computer Vision (IJCV), 103:267– 305, 2013.
• D. Martinec and T. Pajdla. Robust rotation and translation estimation in multiview reconstruction. In CVPR, pages 1– 8. IEEE, 2007.
• K. Wilson, D. Bindel, and N. Snavely. When is rotations averaging hard ? In ECCV, pages 255–270. Springer, 2016.

Martinec建议根据Frobenius范数解决此问题，而Govindu建议将旋转平均问题转换为李代数平均。

在此基础上，结合鲁棒的L1优化可获得更好的结果。

最近，威尔逊发现了两个影响旋转估计精度的因素，一个是EG结构，另一个是对极几何精度，并且建议将它们均匀分布时首先聚集在一起。但是，他们没有描述基于此理论如何有效地对图像进行分组和合并。 受此理论分析的启发，我们提出了一种基于社区的轮换平均方法，该方法可自动确定何时以及如何进行聚类，然后进行贪婪的合并步骤。

位移平均：

许多线性方法提出了通过矩阵分解来求解摄像机位置的方法。 尽管有效，但这些方法对极线几何外点值敏感。 因此，许多全局式sfm方法首先仔细的过滤了错误的边缘。Zach提出通过循环一致性检查来过滤边缘，Wilson提出了一种类似于哈希的方法，称为1DSfM。然而这种方法需要大量的成对关联\((O(n^2))\)，比起滤波，某些方法通过局部BA或多视点轨迹一致性来细化对极关系。

其他方法可以同时解决场景点和相机中心。 这样，不仅解决了共线运动问题，而且将所有摄像机融合到相连的平行刚度图中。

另外，有些方法融合了辅助成像信息以获得相机中心。尽管它们高效且可扩展，但它们严重依赖于辅助信息。

Overview of Hybrid SFM

考虑到增量方法通常是由于通过BA进行了反复优化，因此更加鲁棒和准确，但是如果图像数据集很大，其计算量就很大，而全局方法则适合于估计所有旋转，但在摄像机中心估计时由于外点的存在容易出现错误，我们在此利用增量方案和全局方案的优势来提出一个混合SfM。

正如上图中所显示的，我们的系统的输入是对极几何图像（EG），其中包括每个对极边上的成对匹配，以及从本质矩阵分解估计的相应成对几何。

例如，本质矩阵的边缘\(edge(i,j)\)对相对旋转\(R_{ij}\)和相对位移方向\(t_{ij}\)（注意这里只有方向，没有尺度），并受以下公式的约束。

\[\begin{eqnarray} R_{ij} &=& R_jR_i^T\\ \lambda_{ij}t_{ij} &=& R_j(C_i-C_j) \end{eqnarray} \]

其中\(C_i\)和\(R_i\)对应于相机中心和图像\(i\)的旋转。

全局摄像机旋转和相对旋转之间的方程式可以首先转换为李代数空间，然后使用L1优化来求解，但是，全局旋转平均的精度对EG的结构和成对几何的精度均敏感。

因此在图中，我们的混合SfM的第一个模块中，我们提出了一种基于社区的旋转平均方法来考虑这两个因素。

对于相机中心估计，因为比例因子\(\lambda_{ij}\)未知，所以很难直接估计摄像头中心。

论文《O. Ozyesil and A. Singer. Robust camera location estimation by convex programming. In CVPR, pages 2674–2683. IEEE, 2015.》 证明基本矩阵只能确定平行刚性图中的摄像机位置。

另外，位移估计对错误的特征匹配很敏感，因此在图中的第二个模块中，我们使用了一种增量方式，它可以从RANSAC方法中受益，以排除错误的特征匹配，从而估计摄像机的中心。当无法再添加摄像机时，将执行最终的BA，以完善所有摄像机的固有参数，摄像机的姿势和场景结构。

Global Rotation Estimation

对于顺序图像，连接通常均匀分布。

但是对于无序图像，例如来自Internet的大量图像，摄像机的分布通常是不均匀的，例如 感兴趣的地方通常会受到更多关注。结果是，如果场景中有许多感兴趣的建筑物，则建筑物之间的整体连接会变得稀疏，而每座建筑物的连接都更加密集。

为了解决摄像机分布不均的问题，我们提出了一种受复杂网络分析技术启发的自动分组方法。 然后，对每个社区执行旋转平均，然后执行对齐步骤以将它们融合为一个统一的坐标系。

社区发现

社区发现已被广泛用于复杂网络分析，旨在将图分为内部密集连接和外部稀疏连接的组。

令\(A_{ij}\)为对极几何图形（EG）相邻矩阵的元素。

如果摄像机i和摄像机j之间存在边，则\(A_{ij} = 1\)，否则\(A_{ij} = -1\)。

EG中的节点i的度数是与其连接的摄像机的数量，表示为\(d_i = \sum\limits_jA_{ij}\)。让\(m = \frac{1}{2}\sum\limits_{ij}A_{ij}\)，作为EG中边的总数。

如果EG被随机化而没有社区结构，那么相机i和相机j之间存在边的概率为\(\frac{d_id_j}{2m}\)，要测量EG与随机图之间的社区内连接分数的差异，我们使用《A. Clauset, M. E. Newman, and C. Moore. Finding com- munity structure in very large networks. Physical Review E, 70(6 Pt 2):264–277, 2005.》中提出的模块化指标Q。

假设摄像机i属于社区\(S_p\)，摄像机j属于社区\(S_q\)，那么Q可以被定义为：

\[Q= \frac{1}{2m}\sum\limits_{ij}(A_{ij}-\frac{d_id_j}{2m})\delta(S_p,S_q) \]

如果\(S_p = S_q\)，则\(\delta(S_p,S_q) = 1\)，否则\(\delta(S_p,S_q)= 0\)。

为了增强具有更多匹配项的良好边缘的影响，我们使用相邻矩阵的权重和边缘权重\(A_{ij}\)被设定为\(\sqrt{N_{ij}}\)。

\(N_{ij}\)是相机i和相机j之间的特征匹配内线数（feature match inliers）。

RANSAC算法的基本假设是样本中包含正确数据(inliers，可以被模型描述的数据)，也包含异常数据(outliers，偏离正常范围很远、无法适应数学模型的数据)，即数据集中含有噪声。

为了划分EG，我们假设每个节点首先属于一个单独的社区，然后迭代地加入各个单独的社区，这些社区的合并导致Q值的最大增长。模块化在整个树状图的生成过程中具有单个峰\(Q_{max}\)，这表明最重要的社区结构。

在实践中，我们发现\(Q_{max}> 0.4\)表示EG具有显着的社区结构。因此，当峰值大于0.4时，我们将得出分区结果。

否则，当\(Q_{max} <0.4\)时，所有摄像机都被视为一个社区。

旋转平均

对于每个社区，《A. Chatterjee and V. M. Govindu. Efficient and robust large- scale rotation averaging. In ICCV, pages 521–528. IEEE, 2013.》中提出的全局旋转平均方法用于旋转平均。结果是，每个社区的估计旋转都在不同的坐标系下。 当我们有两个或更多个社区时，应进行对齐以将它们置于统一的坐标系中。

任意一对社区之间的变换（transformation）都是SO（3）中的旋转矩阵，但是在原始对极几何图中，两个社区之间通常有很多边。因此，我们提出了一种投票方案，以找到每对社区的最佳变换，对于两个社区之间的每个边缘，我们都有一个可能的旋转变换候选，然后，基于该候选旋转，计算这对社区之间其他边缘的残差。

最好的变换是具有最多inliers的变换，其中inliers定义为残角小于15度的边。（这里没明白）

在获得连接社区之间的所有转换后，原始对极图被简化为加权社区图，其中节点对应于社区，并且边沿将社区与连接联系起来，每个边上的权重定义为对应的最佳变换的inliers的比率。

我们将参考坐标系设置为度数最大的节点，并为此对齐方式构建该社区图的最大生成树（MST）。 基于MST，其他社区的旋转与参考社区保持一致。

下图展示了我们在Gendarmenmarkt数据集上基于社区的旋转平均结果，其中每条曲线表示全球相机旋转误差的累积分布函数（CDF）。

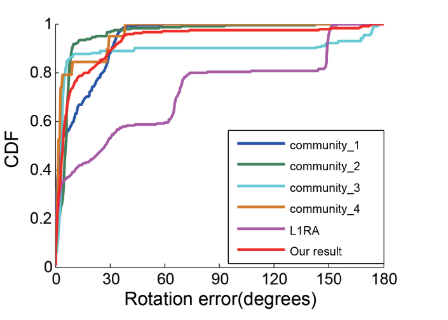
根据L1RA的结果，该结果对应于所有摄像机都被视为唯一社区的情况，我们可以看到其旋转估计是错误的。但是，将其划分为四个社区后，每个社区的估计轮换变得更加准确。我们的最终结果以红色显示，这大大提高了相机的旋转精度。

Incremental Centers Estimation

一旦实现了每个摄像机的旋转，出于稳定性考虑，我们将以递增（Incremental）的方式估算摄像机的中心。随着估计过程的进行，场景结构也被重建。

在接下来的内容中，我们介绍了三个约束条件，以便首先选择一对好的摄像机进行初始重建。然后，基于估计的场景结构和跨图像的轨迹之间的对应关系，通过修改后的BA来迭代估计和优化摄像机中心。

初始相机选择和重建

为了获得良好的初始重建效果，一对摄像机应满足三个约束：更多的特征匹配，更宽的基线和准确的摄像机姿势。

EG中的所有边缘都可以视为我们最初选择相机对的候选对象。 因此，我们通过用这三个约束标记每个边缘来增强EG。

首先，每个边上的特征匹配的内部数量记录了由5点算法验证过的EG中的值。

然后，在已知旋转的情况下，摄像机i和摄像机j之间的成对归一化特征匹配\(（pi，pj）\)的角度可通过以下公式计算：

\[acos(R_i^T,p_i,R_j^T,p_j) \]

对于EG中的每个边缘，我们计算与其特征匹配相对应的所有角度，并记录中间值以指示基线的长度。

由于不知道地面真实镜头的位姿，因此我们无法找到具有最佳相机位置的图像对。然而每个社区中的平均旋转可以看作是为每个摄像机找到最佳的摄像机旋转，从而将其连接的边缘的中间残差最小化，这意味着摄像机连接的边缘越多，估计的旋转可能越准确。

设\(n_i\)是EG中相机i的邻居数，相机i和相机j之间的一条边的相机位姿准确性表示为：

\[\sqrt{(n_i^2+n_j^2)/2} \]

基于每个边缘上的这三个指标，我们提出了一种级联方案(cascaded scheme)来选择初始摄像机对。我们认为摄像机的位姿精度首先是为了获得准确的初始重建。

但是，即使使用精确的相机位姿，如果基线很小，则重建仍然会受到影响。因此，针对场景结构问题，我们选择具有第二优先权的基线因子。

最后，我们考虑匹配内线的数量。

在实践中，首先将位姿精度指标以降序排序，我们仅选择前\(\alpha_1\)个边（在我们的工作中，\(\alpha_1\)设置为60％）。 然后，在初始摄像机选择中舍弃中间角度小于10度的边缘，以避免纯旋转问题。最后，对于所有其余边缘，我们选择图像匹配数量最大的边缘。

对于选定的初始对相机i和相机j，我们重新计算其相对旋转\(R_{ij} = R_jR_i^T\)，其中\(R_i\)和\(R_j\)是旋转平均的结果。

然后，通过固定这个新的相对旋转，通过求解线性系统\(p_j^T[t_{ij}]_{\times}R_{ij}p_i = 0\)来定义相应的相对平移\(t_{ij}\)。这个式子需要两个点来求解。

基于RANSAC方法，\(t_{ij}\)被细化，然后通过从图像点到其心新的极线的距离重新评估此图像对之间的特征匹配。验证之后，特征匹配的内部区域由修改后的BA进行三角剖分和改善（ triangulated and refined），该BA仅改善相机中心和当前重建的场景结构。

相机注册

基于已知的相机旋转，相机的中心可以仅仅通过两个场景点估计出来，原因是对于具有已知旋转及其两个场景点的摄像机，来自场景点的两条投影射线都穿过摄像机中心。

例如：相机i和场景里的可见点\(X_j = \{X_{jx},X_{jy},x_{jz}\}\)及其对应的图像坐标\(x_{ij}\)，投影方程可以转换为

\[X_j - C_i = \lambda R_i^TK_i^{-1}x_{ij} \]

令\(h_i = \{h_{ix},h_{iy},h_{iz}\} = R_i^TK_i^{-1}x_{ij}\)，相机中心\(C_i = \{C_{ix},C_{iy},C_{iz}\}\)，然后我们得到以下两个独立方程：

\[(X_{jx} - C_{ix})h_{iz} = (X_{jz}-C_{iz})h_{ix}\\ (X_{jy} - C_{iy})h_{iz} = (X_{jz} - C_{iz})h_{iy} \]

由于相机中心的自由度为3，我们至少需要两个点。对于每个观察到两个以上场景点的摄像机，我们使用RANSAC技术找到最佳的摄像机中心，该中心的可见场景点像素的数量最多，其投影误差小于\(\gamma_1\)像素。

然后，进一步检查两个约束条件：内线数应大于\(\beta_1\)，相应的内线比应大于\(\beta_2\)。

如果两个条件都满足，我们认为摄像机中心估计成功。（在我们的工作里，\(\beta_1 = 16,\beta_2 = 60\%\)）

有些时候可见点的数量很大（例如多于30个），估计的摄像机中心仍然是错误的，因为某些估计的摄像机旋转可能不够准确。在这种情况下，我们使用P3P的方法找到一个合适的相机位姿。同样，如果inliers的数量和比率仍然满足上述两个约束，我们将更新相应的相机旋转和中心。

请注意，由于摄像机旋转是通过场景点估算的，因此它仍处于原始旋转坐标系中。

三角测量

在将一些新摄像机添加到SfM系统后，所有具有2个以上已校准摄像机的轨道均被三角测量。 在这里，我们使用基于RANSAC的三角测量方法。 对于每次迭代，我们随机选择两个可见的视图，然后检查两个投影射线之间的角度。如果该角度大于3度，则认为当前条件良好，并使用DLT方法进行三角剖分。然后，在获得场景点三角测量后，将同时检查其一致的测量次数和相应的视图cheirality 。

cheirality是多视图几何中代表着3D点的正景深约束

假设存在一个3D点\(X_w\)，一个相机\(C\)，如果\(X_w\) 能被\(C\)观测到，也就是说该点的景深相对于这个相机是正的(如果相机z轴定义为和相机朝向相同)，那就说明这个点满足cheirality constraint

cheirality constraint一般可以用来判断匹配点对是否正确，并经常用于从本质矩阵\(E\)的四组分解中筛选出正确的一组\(R,t\)

相关论文

请注意，轨道中所有校准摄像机的cheirality应为正，如果相应的重投影误差小于\(\gamma_1\)像素，则轨道中的测量值被认为与当前场景点估计一致。

对于每个轨道，我们找到具有最多一致测量值的最佳场景点。

优化相机中心和场景结构

为了减少累积错误的影响，我们在每个摄像机添加和三角测量过程之后进行BA。

为了解决潜在的异常值，我们的BA中将Huber函数用作损失函数。

为了确保在相机添加过程中固定相机旋转坐标系，我们仅通过保持固有参数和相机旋转不变来微调相机中心并重建场景结构。 因此，修改后的BA公式为：

\[\mathop{minimize}\limits_{C_i,X_j} \sum\limits_{i=1}^N \sum\limits_{j=1}^M \delta_{ij}||x_{ij} - \gamma(K_i,R_i,C_i,X_i)||_{huber} \]

• 如果相机i可以观察到点j，则\(\delta_{ij} = 1\)，否则\(\delta_{ij} = 0\)
• \(K_i,R_i,C_i\)分别表示相机的内参矩阵和相机i的中心
• \(\gamma(K_i,R_i,C_i,X_i)\)是投影函数
• \(x_{ij}\)表示测量的2D图像点位置。

与VSFM和COLMAP相似，我们对轨道重新三角化以减少累积的误差，因为在BA后摄像机中心变得更加准确。

使用通过重新三角测量计算的新场景结构，我们执行另一个BA以获得更准确的相机位姿。 在此BA之后，再次执行重新三角测量步骤，并对具有大投影误差的轨道进行滤波。

实验

实验ceres solver进行BA调整，将用于内部判断的错误阈值\(\gamma_1\)设置为16个像素。

顺序图像数据评估

许多全局式sfm方法会使用三约束同时估算初始相机位姿，因此它们对漂移误差具有鲁棒性，但是通常会留下一些未经校准的图像。

增量SfM方法对异常值具有鲁棒性，并且不依赖于图像三元组，但是无法避免累积的错误。

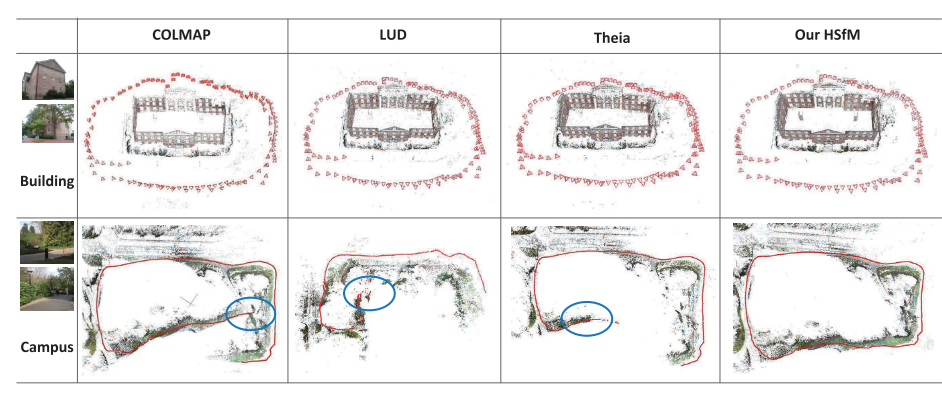
从建筑的结果来看，里面比较干净。通过对极几何，我们可以看到，所有比较方法都可以成功地重建场景。

但是，对于数据集Campus来说，有很多树，并且相机轨迹是一个循环。 该数据集的成对几何估计被污染，并且由于匹配的树，很容易出现许多异常轨迹。 从上图第二行的结果中，我们可以看到COLMAP和Theia有明显的漂移误差，使得无法获得闭环。 在

另外，由于摄像机的轨迹近似为线性运动，并且成对的几何体稀疏，因此基于平移的方法LUD在该数据集上失败了。

相比之下，我们的结果实现了闭环并且对共线摄像机运动有效。

无序图像数据评估

为了演示我们的混合SfM

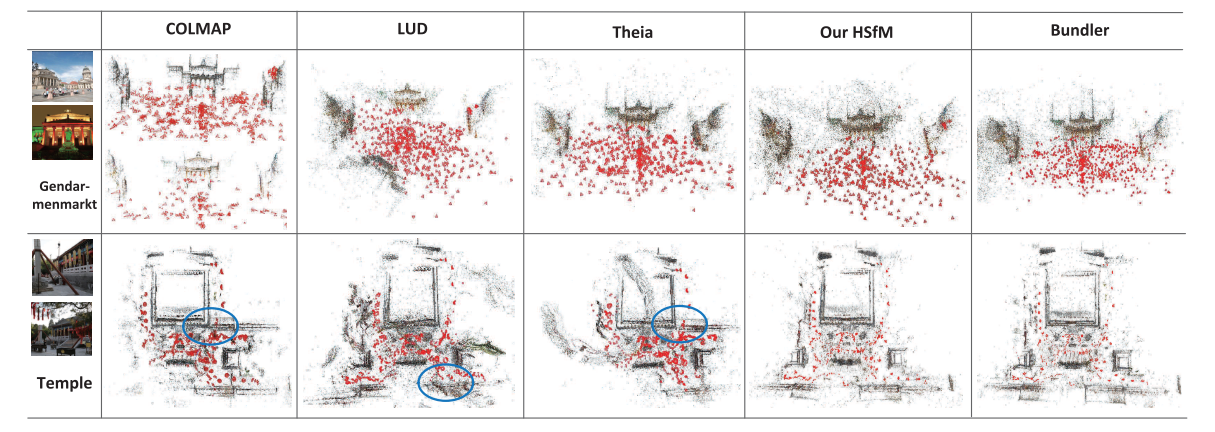
我们使用数据集包含十二组中规模数据，两个大型数据：Piccadilly和Trafalgar，以及具有对称架构的具有挑战性的数据集Gendarmenmarkt。 我们还在数据集Temple上进行测试，该数据集包含许多对称结构和场景中的树木。

我们将我们的方法与四个最先进的全球方法进行比较。

我们可以看到，在大多数情况下，我们的混合SfM方法可重构最多数量的相机，这表明我们的方法对异常值更为鲁棒。 对于校准精度，我们的方法可达到与这些最新方法相似或更好的精度。并且我们可以看到我们的方法比最新的增量方法要快得多，并且其效果与全局方法相似或更好。

考虑到准确性和时间成本，我们可以得出结论，虽然我们的混合SfM继承了增量方式的鲁棒性，但它也具有全局方式的速度优势。