《A Compact Algorithm for Rectification of Stereo Pairs》学习笔记

参考自：https://blog.csdn.net/weixin_39675633/article/details/103931635

A Compact Algorithm for Rectification of Stereo Pairs

Introduction

给定一对双目图像，校正确定每个图像平面的变换，以使成对的共轭对极线变为共线并平行于一个像轴。

校正后的图像可以视为是通过旋转原始相机获得的新双目设备得到的。

校正使得计算双目匹配变得更加容易，因为匹配搜索被约束到了一维空间而不是二维空间。

假设：双目设备已经标定（相机的外参（外部参数包括位置和方向）是已知的）。

当从稠密的双目中重建3D对象的形状时，在实践中必须进行校准（标定）。然而在计算机视觉文献中几乎没有可用的方法。

本文提出了一个新的算法可用于校正已标定相机，该相机（一般通用相机）不受几何约束。

CameraModel

针孔相机通过光学中心C和图像平面R进行建模。一个3D点W投影到图像平面\(M \in R\)，它是光心C和W连线与图像平面的交点。

包含C且与R正交的线称为光轴，与R的交点称为焦点（principal point），C与R之间的距离称为焦距（focal length）

\(w = [x\quad y\quad z]^T\)是世界坐标系中W的坐标，\(m = [\mu \quad v]^T\)是图像平面中M的像素坐标。这种从3D坐标到2D坐标的映射称为透视投影。

可以用其齐次坐标的坐标线性变换表示。

令\(\tilde{m} = [\mu\quad v \quad 1]^T\) 和 \(\tilde{w} = [x \quad y\quad z]^ T\)分别是M，W的齐次坐标，然后透视变换由\(\tilde{P}\)给出：

\[\lambda \tilde{m} = \tilde{P} \tilde{w} \]

其中\(\lambda\)是尺度因子。因此相机可通过透视投影矩阵（PPM）\(\tilde{P}\)来表示，\(\tilde{P}\)可以由QR分解成为：

\[\tilde{P} = A[R|t] \]

A仅仅依赖内部参数（内参矩阵）由下面的形式

\[A = \left[ \begin{matrix} \alpha_u & \gamma & u_0\\ 0 & \alpha_v & v_0\\ 0 & 0 & 1 \end{matrix} \right] \]

其中\(\alpha_u = -fk_u\)，\(\alpha_v = -fk_v\)分别是水平和垂直方向上的像素焦距长度（f 是焦距长度，单位为毫米，\(k_\mu,l_v\)是沿\(\mu,v\)轴每毫米有效的像素数）

\((\mu_0, v_0)\)是主点像素坐标，它是光轴与像平面的交点，\(\gamma\)是\(\mu-v\)非正交的因子。

将PPM重新写作:

\[\tilde{P} = \left[ \begin{matrix} q_1^T & q_{14}\\ q_2^T & q_{24}\\ q_3^T & q_{34}\\ \end{matrix} \right] = [Q|q] \]

在笛卡尔坐标系（直角坐标系）中，可写为

\[\begin{cases} \mu = \frac{q_1^Tw + q_{14}}{q_3^Tw + q_{34}}\\ v = \frac{q_2^Tw + q_{24}}{q_3^Tw + q_{34}} \end{cases} \]

平行于像平面与过光心\(C\)的平面叫做焦平面，\(C\)的c坐标在世界坐标系W可表示为

\[c = -Q^{-1}q \]

推导如下：

设相机坐标系的圆点在世界坐标系中的表示为c，由透视投影可得\((0,0,0)^T = [Q|q]\tilde{c}\)

从而\(Q\tilde{c}+q = 0 \longrightarrow c = -Q^{-1}q\)

因此\(\tilde{P}\)可重写为：

\[\tilde{P} = [Q|-Qc] = A[R|-Rc] \]

与像点M相关的光线是M C，也即3-D点的集合{\(w:\tilde{m} = \tilde{P}\tilde{w}\)}，参数化形式为：

\[w = c + \lambda Q^{-1}\tilde{m} \]

推导如下：

\(\lambda \tilde{m} = \tilde{P}\tilde{w} = [Q|-Qc]\tilde{w} = Q\tilde{w} - Qc \longrightarrow w = c + \lambda Q^{-1}\tilde{m}\)

考虑有两个针孔相机组成的双目设备

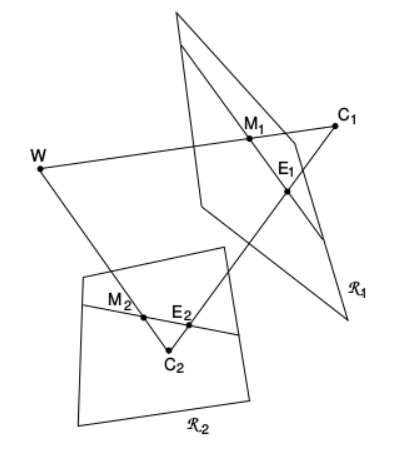
\(C_1, C_2\)分别是左目和右目相机的光心。将3D点W投影到两个图像平面上，构成共轭点对\(M_1,M_2\)，

给定左图像平面中的点\(M_1\)，将其在右图像中的共轭点约束到\(M_1\)对极线上。

因为\(M_1\)可能是它所在光线上的任何一点的投影。对极线是\(M_1\)的光线经过\(C_2\)的投影线。

一个像平面中的所有对极线都通过称为“极点”的公共点\((E_1,E_2)\)，这是另一台相机的光学中心的投影。

当\(C_1\)是右相机的焦平面上，右极点在无穷远，在右图像中极线形成一束平行线。一种简单的情况是，两个极点都在无穷远处，基线在两个焦平面上，像平面平行于基线时就会出现该情况，极线在两个图像中形成一束平行线。可以变换任何一对图像，以使对极线在每个图像中平行且水平。 此过程称为校正。

校正相机矩阵

假设立体设备已经标定，透视投影矩阵\(\tilde{P}_{o1}\)和\(\tilde{P}_{o2}\)已知。校正的思想是定义两个新的投影矩阵\(\tilde{P}_{n1}\)和\(\tilde{P}_{n2}\)，通过绕着各自的光轴旋转，直到焦平面共面，从而包含基线。这就保证了极点在无穷远，因此极线平行。

要具有水平极线，基线必须平行于两个相机的新的X轴，另外为了有一个正确的校正，共轭点必须有相同的垂直坐标（即校正后匹配点的新y轴坐标相等），这是通过新相机具有相同的内部参数来实现的。注意，校正后焦距相同，像平面也共面。

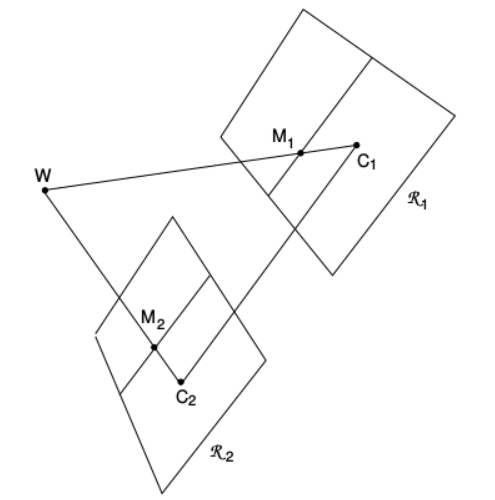
总结：新透视矩阵的位置（即光心）与校正之前的相机的光心相同，然后新的方向与校正之前不同，它是由校正前的相机经过合适的旋转得到的。两个相机的内参矩阵是相同的。因此，两个新的透视投影矩阵仅在其光学中心不同，可以将它们视为沿其参考系统的X轴平移的单个相机。

重写新的透视投影矩阵：

\[\tilde{P}_{n1} = A[R|-Rc_1]\qquad \tilde{P}_{n2} = A[R|-Rc_2] \]

上面两个透视投影矩阵中的A是相同的，可以被任意选择。

光学中心\(c_1\)和\(c_2\)由旧的光学中心给出，通过式\(c = -Q^{-1}q\)计算。

矩阵R是相机的姿态，通过行向量可表示为

\[R = \left[ \begin{matrix} r_1^T\\r_2^T\\r_3^T \end{matrix} \right] \]

\(r_1^T,r_2^T,r_3^T\)分别为相机参考系的X,Y,Z轴在世界坐标系中的表示。

有以下结论：

1. 新的X轴平行于基线：\(r_1 = (c_1 - c_2) / ||c_1 - c_2||\)
2. 新的Y轴正交于X轴和k：\(r_2 = k \times r_1\)
3. 新的Z轴正交于XY平面：\(r_3 = r_1 \times r_2\)

k是一个任意单位向量，将新Y轴的位置固定在与X正交的平面中,我们将其等于旧左矩阵（校正前矩阵）的Z轴单位向量（即\(R_{o1}\)的第三行的向量，它是左相机Z轴在世界坐标系下的表示）

但是，当光轴平行于基线时，即纯向前运动时，该算法将失败。

为了校正左图像，需要计算\(\tilde{P}_{o1} = [Q_{o1}|q_{o1}]\)到\(\tilde{P}_{n1} = [Q_{n1}|q_{n1}]\)映射变换。寻求的变换是由\(3 \times 3\)矩阵\(T_1 = Q_{n1}Q_{o1}^{-1}\)给出的共线性变换。

对于任意一个3D点w有

\[\begin{cases} \tilde{m}_{o1} = \tilde{P}_{o1}\tilde{w}\\ \tilde{m}_{n1} = \tilde{P}_{n1}\tilde{w}\\ \end{cases} \]

光线的表达式如下：

\[\begin{cases} w = c_1 + \lambda_0Q_{o1}^{-1}\tilde{m}_{o1}\\ w = c_1 + \lambda_nQ_{n1}^{-1}\tilde{m}_{n1}\\ \end{cases} \]

从而

\[\tilde{m}_{n1} = \lambda Q_{n1}Q_{i1}^{-1}\tilde{m}_{o1} \]

其中\(\lambda\)是任意的尺度因子（等价于在齐次下相等）。

注意，校正后的图像的像素（整数坐标位置）通常对应于原始图像平面上的非整数位置。 因此，通过双线性插值计算校正图像的灰度值。