Structure from motion 代码实现
部分知识点参考自:https://blog.csdn.net/wphkadn/article/details/85805105
代码部分参考自:https://blog.csdn.net/AIchipmunk/article/details/51232861
solvepnpransac部分参考自:https://blog.csdn.net/lircsszz/article/details/80078730
运动恢复结构代码实现
灵活运用所学基础知识,尝试使用代码实现简单的Structure from motion
全局变量
为了方便调试和使用方便,我将大部分变量设置为了全局变量。
vector<Mat> images; //-- 存放所有图片
vector<vector<KeyPoint>> allKeypoints; //-- 存放所有图片的关键点
vector<Mat> allDescriptors; //-- 存放所有图片的描述子
vector<vector<DMatch>> allMatches; //-- 存放特征点的匹配关系
vector<vector<cv::Vec3b>> allColors; //-- 存放特征点的颜色信息
vector<vector<int>> correspond_pts_idx; //-- 匹配点空间索引
vector<Mat> rotations; //-- 存放所有的旋转矩阵
vector<Mat> translations; //-- 存放所有的平移向量
int img_idx; //-- 存放当前操作的图片索引
Mat K = (Mat_<double>(3,3) << //-- 相机内参矩阵
1520.0, 0.0, 302.2,
0.0, 1520.0, 246.87,
0.0, 0.0, 1.0);
读取图像
由于SFM一次性需要读入很多图像,所以单独使用一个txt文件来存储图像位置。

使用ReadImg函数来读取图片的位置,并存放在图像数组images中
const string path = "/home/linzzz/projects/SlamProjects/image/sfm/";
void ReadImg()
{
//-- 标定所用图像文件的路径
ifstream inImgPath(path + "img.txt");
string temp;
if (!inImgPath.is_open())
{
cout << "没有找到文件" << endl;
}
//-- 读取文件中保存的图片文件路径,并存放在Image数组中
while (getline(inImgPath, temp))
{
images.push_back(imread(temp));
}
}
在这里可以使用imshow函数来判断是否存放成功。
for(auto img : images)
{
imshow("image", img);
waitKey();
}

特征提取
读取完图像之后,需要对图像进行特征提取。
在这里我选择了使用ORB算法来进行特征提取(因为SIFT死活安装不上。。)
allKeypoints.clear(); //-- 每次提取时需要将之前的关键点清空
allDescriptors.clear(); //-- 清空描述子
Ptr<FeatureDetector> detector = ORB::create(1000); //-- 1000是为了提取更多的特征点
Ptr<DescriptorExtractor> descriptor = ORB::create(1000);
//--遍历所有图片
for(auto img : imgs)
{
//-- 如果图片为空,则返回
if(img.empty()) return;
vector<KeyPoint> keypoints; //-- 定义该图片的关键点
Mat descriptors; //-- 定义该图片的描述子
detector->detect(img, keypoints); //-- 特征检测
descriptor->compute(img, keypoints, descriptors); //-- 计算描述子
allKeypoints.push_back(keypoints);
allDescriptors.push_back(descriptors);
vector<Vec3b> color(keypoints.size()); //-- 定义该图片关键点的颜色信息(Vec3b)
//--遍历所有关键点
for(int i = 0; i < keypoints.size(); i++)
{
Point2f &p = keypoints[i].pt; //-- 取出每一个关键点
if(p.x <= img.rows && p.y <= img.cols) //-- 对于每个在图片内部的关键点
{
color[i] = img.at<Vec3b>(p.x, p.y); //-- 存入该点的颜色信息
}
}
allColors.push_back(color);
}
值得一提的是,在以前使用ORB::create时总是使用默认参数,但是ORB::create的参数列表有很多,在这里需要选择合适的参数。
CV_WRAP static Ptr<ORB> create(int nfeatures=500, float scaleFactor=1.2f, int nlevels=8, int edgeThreshold=31,
int firstLevel=0, int WTA_K=2, int scoreType=ORB::HARRIS_SCORE, int patchSize=31, int fastThreshold=20);
| 参数名 | 类型 | 含义 | 描述 | 默认值 |
|---|---|---|---|---|
| nfeatures | int | 要查找的最大关键点数 | 500 | |
| scaleFactor | float | 金字塔抽取率 | 必须大于1。ORB使用图像金字塔来查找特征,因此必须提供金字塔中每个图层与金字塔所具有的级别数之间的比例因子。scaleFactor = 2表示经典金字塔,其中每个下一级别的像素比前一级低4倍。大比例因子将减少发现的特征数量。 | 1.2 |
| nlevels | int | 金字塔等级的数量 | 最小级别的线性大小等于input_image_linear_size / pow(scaleFactor,nlevels)。 | 8 |
| edgeThreshold | int | 未检测到特征的边框的大小 | 由于关键点具有特定的像素大小,因此必须从搜索中排除图像的边缘。edgeThreshold的大小应等于或大于patchSize参数。 | 31 |
| firstLevel | int | 确定应将哪个级别视为金字塔中的第一个级别 | 在当前实现中,它应该为0。 通常,具有统一等级的金字塔等级被认为是第一等级。 | 0 |
| WTA_K | int | 用于产生定向的Brief描述符的每个元素的随机像素数 | 可能的值为2、3和4,其中2为默认值。 例如,值3表示一次选择三个随机像素以比较它们的亮度。 返回最亮像素的索引。 由于存在3个像素,因此返回的索引将为0、1或2。 | 2 |
| scoreType | int | 角点类型 | HARRIS_SCORE或FAST_SCORE。 默认的HARRIS_SCORE表示使用Harris角算法对要素进行排名。 分数仅用于保留最佳功能。 FAST_SCORE产生的稳定关键点要少一些,但是计算起来要快一些。 | ORB::HARRIS_SCORE |
| patchSize | int | Brief描述符的patch大小 | 在较小的金字塔层上,特征覆盖的感知图像区域将更大。 | 31 |
| fastThreshold | int | 快速阈值大小 | 20 |
可见, ORB::create()函数支持的参数很多。前两个参数(nfeatures和 scaleFactor)可能是最常用的参数。其他参数一般保持默认值既能获得比较良好的结果。
特征匹配
计算完关键点之后,需要计算每两张图片之间的匹配关系(1-2, 2-3 …. n-1 - n)
思路为:先计算两张的匹配关系,然后通过循环不断重复这个过程。
//-- 先计算两张的匹配关系
void MatchFeatures(Mat &descriptor_1, Mat &descriptor_2, vector<DMatch> &matches)
{
//-- 特征匹配,使用暴力匹配计算Hamming距离
//-- 可选参数
// `BruteForce` (it uses L2 )
// `BruteForce-L1`
// `BruteForce-Hamming`
// `BruteForce-Hamming(2)`
// `FlannBased`
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
vector<DMatch> match; //-- 定义储存匹配信息的match
matcher->match(descriptor_1, descriptor_2, match); //-- 特征匹配
double min_dist = 10000, max_dist = 0; //-- 匹配点对筛选
//-- 找出所有匹配之间的最小距离和最大距离,即是最相似的和最不相似的两组点之间的距离
for(int i = 0; i < descriptor_1.rows; i++)
{
double dist = match[i].distance;
if(dist < min_dist) min_dist = dist;
if(dist > max_dist) max_dist = dist;
}
//-- 当描述子之间的距离大于两倍的距离时,即认为匹配有误,但有时候最小距离会非常小,设置一个经验值30作为下限。
for(int i = 0; i < descriptor_1.rows; i++){
if(match[i].distance <= max(2 * min_dist, 30.0)){
matches.push_back(match[i]);
}
}
cout << matches.size() << endl; //-- 输出特征匹配的个数
//DrawMatchFeatures(matches);
}
为了检测匹配的正确性,定义一个绘制函数来绘制匹配关系
void DrawMatchFeatures(vector<DMatch> matches)
{
//-- 定义特征匹配完的两张图像
Mat img_1 = images[img_idx];
Mat img_2 = images[img_idx+1];
//-- 定义绘制图像
Mat img_match;
//-- 绘制匹配关系
drawMatches(img_1, allKeypoints[img_idx], img_2, allKeypoints[img_idx+1], matches, img_match);
//-- 设置显示窗口类型
namedWindow("match", WINDOW_NORMAL);
//-- 显示图像
imshow("match", img_match);
waitKey();
}
如果不设置nameWindow的类型,则图片很大时则会全屏显示且显示不全,因此归纳总结一些nameWindow第二个参数的类别。(第一个参数要和imshow的第一个参数对应——窗口名)
| 参数 | 作用 |
|---|---|
| WINDOW_NORMAL | 窗口大小可以改变 |
| WINDOW_AUTOSIZE | 窗口大小不可以改变 |
| WINDOW_FREERATIO | 窗口大小自适应比列 |
| WINDOW_KEEPRATIO | 窗口大小保持比例 |
| WINDOW_GUI_EXPANDED | 显示色彩变成暗色 |
| WINDOW_FULLSCREEN | 窗口全屏显示 |
成功显示匹配关系

然后将两张图片的匹配扩展到多张。
//-- 循环匹配两张图像
void MatchFeatures()
{
allMatches.clear(); //-- 清空之前的匹配关系
//-- 这里循环上限为allDescriptors.size() - 1,因为最后一次匹配 i+1 正好匹配到最后一张。
for(int i = 0; i < allDescriptors.size() - 1; i++)
{
img_idx = i; //-- img_idx描述当前匹配的是第几张图像,方便后续操作
cout << "Matching images " << i + 1 << " - " << i + 2 << endl;
vector<DMatch> matches;
MatchFeatures(allDescriptors[i], allDescriptors[i+1],matches); //-- 匹配当前图像和下一张图像
allMatches.push_back(matches); //-- 存入匹配关系
}
}
计算匹配点
//-- 计算匹配点
//-- 把匹配点转换为vector<Point2f>的形式
void MatchPoints(vector<KeyPoint> &keypoints_1, vector<KeyPoint> &keypoints_2,
vector<DMatch> &matches, vector<Point2f> &p_1, vector<Point2f> &p_2)
{
p_1.clear();
p_2.clear();
for(int i = 0; i < matches.size(); i++)
{
p_1.push_back(keypoints_1[matches[i].queryIdx].pt);
p_2.push_back(keypoints_2[matches[i].trainIdx].pt);
}
}
//-- 计算匹配颜色
void MatchColors(vector<Vec3b> &keycolors_1, vector<Vec3b> &keycolors_2,
vector<DMatch> &matches, vector<Vec3b> &c_1, vector<Vec3b> &c_2)
{
c_1.clear();
c_2.clear();
for(int i = 0; i < matches.size(); i++)
{
c_1.push_back(keycolors_1[matches[i].queryIdx]);
c_2.push_back(keycolors_2[matches[i].trainIdx]);
}
}
这里需要额外说明一下queryIdx和trainIdx的含义:
- queryIdx \(\longrightarrow\)是测试图像的特征点描述符(descriptor)的下标,同时也是描述符对应特征点(keypoint)的下标。
- trainIdx \(\longrightarrow\) 是样本图像的特征点描述符的下标,同样也是相应的特征点的下标。
需要先说明keypoints和matches的关系。
每一张图像都会有一组特征点,两张图像之间的两组匹配点会有一对匹配关系。DMatch作为一个结构体用于存放匹配关系。
DMatch中有queryIdx和trainIdx两个量,从一个简单的for循环来看
for(int i = 0; i < matches.size(); i++)
{
p_1 = keypoints_1[matches[i].queryIdx].pt;
p_2 = keypoints_2[matches[i].trainIdx].pt;
}
假设一共有5对匹配关系,即matches.size() = 5,两幅图像分别有20个关键点,即keypoints_1.size() = keypoints_2.size() = 100
那么会有
| i | queryIdx | trainIdx |
|---|---|---|
| 0 | 0 | 9 |
| 1 | 2 | 2 |
| 2 | 4 | 15 |
| 3 | 5 | 13 |
| 4 | 8 | 7 |
可以看到queryIdx是递增的,但不是每次自增1,因为queryIdx表示的是第一幅图象中关键点中有匹配关系的点的下标。是从0开始向后搜索的,所以是递增的。又因为不是每个关键点都有匹配关系,所以不是每次自增1,而是自增到下一个有匹配关系的关键点的下标。
而trainIdx是乱序的,因为在第一幅图像中的关键点的匹配点在第二幅图像的关键点中不一定是哪一个,有可能是keypoints_2[7],也有可能是keypoints_2[11],所以需要找一个最合适的匹配关系,将其下标作为trainIdx。
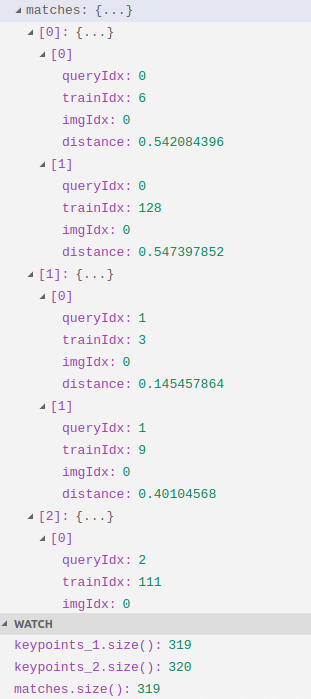
可以看出 queryIdx是按顺序增大的, 相应的trainIdx是不断跳变的
可以从matches[0]看出,这里的queryIdx是指第0张图的第0个特征点匹配到了第1张图的第6个特征点(距离最近),同时第0张图的第0个特征点匹配到了第1张图的第128个特征点(距离第2近)。
于是 queryIdx 是你想要为“它”找到匹配结果的“它”的索引。 trainIdx是 “它”的匹配结果的索引。
计算本质矩阵分解Rt
//-- 传入的p_1和p_2即为上一步计算出的匹配点
void PoseEstimation(Mat &K, Mat &R, Mat &t, vector<Point2f> &p_1, vector<Point2f> &p_2, Mat &mask)
{
// 定义焦距和光心位置
// K = [fx, 0, ux,
// 0, fy, uy,
// 0, 0, 1]
// 其中fx和fy分别为x和y方向上的焦距,在计算时可以取平均作为整体焦距。
// ux和uy为光心的x,y坐标
double focal_lenth = 0.5 * (K.at<double>(0) + K.at<double>(4));
Point2f principal_point(K.at<double>(2), K.at<double>(5));
Mat E = findEssentialMat(p_1, p_2, K, RANSAC, 0.999, 1.0, mask); //-- 可以传入整个内参矩阵,也可以分别传入焦距和光心位置。
//Mat E = findEssentialMat(p1, p2, focal_length, principle_point, RANSAC, 0.999, 1.0, mask);
if(E.empty()) //-- 如果计算出的本质矩阵为空,输出错误信息并退出
{
cout << "!!!!!!!!!Err:EssentialMat Error!!!!!!!!!!" << endl;
exit(0);
}
double feasible_count = countNonZero(mask); //-- 得到非零元素,即数组中的有效点
if(feasible_count <= 15 || (feasible_count / p_1.size()) < 0.5) //-- 对于RANSAC而言,outlier数量大于50%时,结果是不可靠的。
{
cout << "!!!!!!!!!Err:outlier Points are greater than 50\%!!!!!!!!!!" << endl;
exit(0);
}
recoverPose(E, p_1, p_2, R, t, focal_lenth, principal_point); //-- 分解本质矩阵,获得相对变换
}
简单解释一下传入内参矩阵的findEssentialMat各参数说明:
CV_EXPORTS_W Mat findEssentialMat( InputArray points1, InputArray points2,
InputArray cameraMatrix, int method = RANSAC,
double prob = 0.999, double threshold = 1.0,
OutputArray mask = noArray() );
| 参数 | 类别 | 含义 | 描述 | 默认值 |
|---|---|---|---|---|
| cameraMatrix | InputArray | 相机内参矩阵 | 此功能假设points1和points2是具有相同摄像机矩阵的摄像机的特征点 | 无 |
| method | int | 计算本质矩阵的方法 | RANSAC 或 LMedS | RANSAC |
| prob | double | 估计矩阵正确的概率 | 仅用于RANSAC或LMedS方法的参数 | 0.999 |
| threshold | double | 点到极线最大距离 | 距离(以像素为单位)。超出此点时,该点被视为异常值,不用于计算最终的基本矩阵。 根据点定位精度,图像分辨率和图像噪声的不同,可将其设置为1-3。 | 1.0 |
| mask | OutputArray | 输出N个元素数组 | 数组中每个元素对于异常值设置为0,对其他点设置为1。 | noArray() |
三角测量
在上一步之后,我们得到了R和t,接下来我们将使用三角测量来恢复图像的深度。
首先来看一下opencv内置的三角变换函数triangulatePoints
CV_EXPORTS_W void triangulatePoints( InputArray projMatr1, InputArray projMatr2,
InputArray projPoints1, InputArray projPoints2,
OutputArray points4D );
通过观察参数,可以发现需要输入四个矩阵,两张图像的投影矩阵proj1和proj2和两个图像的匹配点p1和p2。
这里p1和p2在之前已经进行过计算(MatchPoints)
主要来思考如何计算投影矩阵proj
一共有两种思路:
- 使用opencv的函数stereoRectify()进行计算。
- 手动计算——外参与内参的乘积。
我们使用的是第二种方法,手动进行计算。
void Reconstruct(Mat &K, Mat &R_1, Mat &t_1, Mat &R_2, Mat&t_2, vector<Point2f> &p_1, vector<Point2f> &p_2, vector<Point3d> &p)
{
Mat proj1(3, 4, CV_32FC1); //-- 定义投影矩阵
Mat proj2(3, 4, CV_32FC1);
R_1.convertTo(proj1(Range(0, 3),Range(0,3)), CV_32FC1); //-- 外参数R1 t1 R2 t2
t_1.convertTo(proj1.col(3), CV_32FC1); //-- convertTo是把第一个矩阵的值复制给第二个,即proj1 = R1
R_2.convertTo(proj2(Range(0, 3),Range(0,3)), CV_32FC1);
t_2.convertTo(proj2.col(3), CV_32FC1);
//经过上述计算后,proj1 = [R|t]的形式
Mat fK; //-- 内参数K
K.convertTo(fK, CV_32FC1);
proj1 = fK * proj1; //-- 内参 x 外参 计算投影矩阵
proj2 = fK * proj2;
Mat pts_4d;
triangulatePoints(proj1, proj2, p_1, p_2, pts_4d); //-- 三角测量,得到四维向量点pts_4d,后续需要归一化
p.clear();
p.reserve(pts_4d.cols);
for (int i = 0; i < pts_4d.cols; i++) {
Mat x = pts_4d.col(i);
x /= x.at<float>(3, 0); // 归一化
Point3d p_3(
x.at<float>(0, 0),
x.at<float>(1, 0),
x.at<float>(2, 0)
);
p.push_back(p_3); //-- 将归一化之后的点存入p
}
}
经过以上步骤之后,p.z即为该点像素的深度值。
初始化
首先进行假设:用于多目重建的图像是有序的,即相邻图像的拍摄位置也是相邻的。
两个相机之间的变换矩阵可以通过findEssentialMat以及recoverPose函数来实现,设第一个相机的坐标系为世界坐标系,现在加入第三幅图像(相机),如何确定第三个相机(后面称为相机三)到到世界坐标系的变换矩阵呢?
如果沿用双目重建的方法,即在第三幅图像和第一幅图像之间提取特征点,然后反复调用findEssentialMat和recoverPose。但是随着图像数量的增加,新加入的图像与第一幅图像的差异可能越来越大,特征点的提取变得异常困难,这时就不能再沿用双目重建的方法了。取一个比较极限的例子,分别在物体的正面和背面拍摄的两张图片,几乎已经找不到特征点了。
换一个新的思路,用新加入的图像和相邻图像进行特征匹配,如第三幅与第二幅匹配,第四幅与第三幅匹配。但是这时就不能继续使用findEssentialMat和recoverPose来求取相机的变换矩阵了,因为这两个函数求取的是相对变换,比如相机三到相机二的变换,而我们需要的是相机三到相机一的变换。
有一个经典的误区:知道相机二到相机一的变换,又知道相机到三到相机二的变换,不就能求出相机三到相机一的变换吗?
实际上是不可以的,因为通过这种方式,你只能求出相机三到相机一的旋转变换(旋转矩阵R)(旋转矩阵实际上是累乘的关系),但他们之间的位移向量T,是无法求出的。这是因为上面两个函数求出的位移向量,都是单位向量,丢失了相机之间位移的比例关系。
那么如何解决这个问题呢?还记得slam14讲中讲到过3d-2d恢复的PnP问题吗?
- 给定:一张已知特征点3D位置的图像,一张二维图像。
- 已知:特征点在世界坐标系(指的是相机最初位置的那个坐标系)下的三维坐标,特征点映射到图像上的二维坐标,三维坐标系中的特征点与二维图像上的匹配关系。
- 未知:相机坐标系在世界坐标系下的位姿,特征点在相机坐标系下的深度。
我们通过对前两张图像进行三维恢复,得到了空间中的三维坐标,此为3d,再加入的第三幅图像,与第二幅图象进行特征匹配,得到一些匹配点,这些匹配点中,肯定有一部分也是图像二与图像一之间的匹配点,此为2d。
这些匹配点的在第三幅图像的像素坐标和在空间中的三维坐标都已知。就可以使用PnP进行求解相机三到相机一的变换矩阵。
在这里,使用的是opencv的solvePnP和solvePnPRansac函数,该函数根据空间中的点与图像中的点的对应关系,求解相机在空间中的位置。两者实现的效果相同,但后者使用了随机一致性采样,使其对噪声更鲁棒。
前两张图像恢复
void Init(Mat K, vector<Point3d> &pts_3d, vector<vector<int>> &correspond_pts_idx, vector<Vec3b> &colors)
{
vector<Point2f> p_1, p_2;
vector<Vec3b> c2;
Mat R, t, mask;
rotations.push_back(Mat::eye(3, 3, CV_64FC1)); //-- 将默认的第一个旋转矩阵(单位阵)存入
translations.push_back(Mat::zeros(3, 1, CV_64FC1)); //-- 将默认的第一个平移向量(0,0,0)存入
MatchPoints(allKeypoints[0], allKeypoints[1], allMatches[0], p_1, p_2); //-- 得到前两张图像的匹配点坐标
MatchColors(allColors[0], allColors[1], allMatches[0], colors, c2); //-- 得到前两张图像的匹配点颜色
PoseEstimation(K, p_1, p_2, mask); //-- 前两张图像计算R,t
CheckPoints(p_1, mask); //-- 筛选有效的匹配点
CheckPoints(p_2, mask);
CheckColors(colors, mask);
Reconstruct(K, rotations[0], translations[0], R, //-- 对前两张图三角测量,计算空间位置坐标
t, p_1, p_2, pts_3d);
rotations.push_back(R); //-- 存入图2针对图1变换的R,t,由PoseEstimation计算得到
translations.push_back(t);
//-- correspond_pts_idx[i][j]代表第i幅图像第j个特征点所对应的空间点在点云中的索引,若索引小于零,说明该特征点在空间当中没有对应点。通过此结构,由特征匹配中的queryIdx和trainIdx就可以查询某个特征点在空间中的位置。
correspond_pts_idx.clear();
correspond_pts_idx.resize(allKeypoints.size()); //-- 大小初始化为与allKeypoints一致
for(int i = 0; i < allKeypoints.size(); i++)
{
correspond_pts_idx[i].resize(allKeypoints[i].size(), -1); //-- 初始化每幅图的特征点对应索引矩阵,默认值为-1
}
int idx = 0; //-- 填写头两幅图像的结构索引
vector<DMatch> &matches = allMatches[0];
for(int i = 0; i < matches.size(); i++)
{
if (mask.at<uchar>(i) == 0) continue; //-- 当前关键点为异常值,则跳过
//-- 如果两个点对应的idx 相等 表明它们是同一特征点 idx 就是pts_3d中对应的空间点坐标索引
correspond_pts_idx[0][matches[i].queryIdx] = idx;
correspond_pts_idx[1][matches[i].trainIdx] = idx;
++idx;
}
其中,CheckPoints函数和CheckColors函数将有效点筛选出来。
还记得之前计算本质矩阵时得到的mask数组吗?里面存放了大量的0和1,当数据为0时说明该点异常,需要舍弃。则通过筛选函数将异常点去除。
void CheckPoints(vector<Point2f> &p1, Mat &mask)
{
vector<Point2f> p1_cpy = p1;
p1.clear();
for(int i = 0; i < mask.rows; i++)
{
if(mask.at<uchar>(i) > 0)
{
p1.push_back(p1_cpy[i]);
}
}
}
void CheckColors(vector<Vec3b> &c1, Mat &mask)
{
vector<Vec3b> c1_cpy = c1;
c1.clear();
for(int i = 0; i < mask.rows; i++)
{
c1.push_back(c1_cpy[i]);
}
}
计算后续图像的3d2d点
void Get3d2dPoints(vector<Point3d> &pts_3d, vector<int> &pts_indices,
vector<Point3f> &obj_points, vector<Point2f> &img_points)
{
obj_points.clear(); //-- 清空三维点数组
img_points.clear(); //-- 清空二维点数组
vector<DMatch> matches = allMatches[img_idx]; //-- 得到已经配对好的最后一张图像和新添加的图像的匹配关系
for(int i = 0; i < matches.size(); i++)
{
int query_idx = matches[i].queryIdx;
int train_idx = matches[i].trainIdx;
int pts_idx = pts_indices[query_idx]; //-- 得到匹配点的索引
if (pts_idx < 0){continue;} //-- 表明之前的所有图像跟这个点没有匹配关系
obj_points.push_back(pts_3d[pts_idx]); //-- 存入新添加图像与已经配对好的图像共有的关键点的3d坐标
img_points.push_back(allKeypoints[img_idx + 1][train_idx].pt); //-- 添加新添加图像与已经配对好的图像共有的关键点的像素坐标
}
}
这里为什么只存储新添加图像与之前图像都共有的匹配点呢?因为之前图像都有的匹配点,说明第一张图像也有,那么这些点就可以用来PnP进行恢复,从而计算新添加图像针对第一张图像的Rt。如果是最后两张图像的匹配点对,与前面的没有对应,那么就无法正常恢复。
PnP
solvePnPRansac(object_points, image_points, K, noArray(), r, t, false);
Rodrigues(r,R); //-- PnP得到的是旋转向量,需要用Rodrigues方法变成旋转矩阵
很简单的一行,opencv自动帮我们计算新添加图像针对第一幅图像的相机变换矩阵。
这里需要仔细深究一下这个函数。
CV_EXPORTS_W bool solvePnPRansac( InputArray objectPoints, InputArray imagePoints,
InputArray cameraMatrix, InputArray distCoeffs,
OutputArray rvec, OutputArray tvec,
bool useExtrinsicGuess = false, int iterationsCount = 100,
float reprojectionError = 8.0, double confidence = 0.99,
OutputArray inliers = noArray(), int flags = SOLVEPNP_ITERATIVE );
| 参数 | 类别 | 含义 | 描述 | 默认值 |
|---|---|---|---|---|
| distCoeffs | InputArray | 畸变系数 | 无 | |
| rvec | OutputArray | 输出的旋转向量 | 使坐标点从世界坐标系旋转到相机坐标系 (注意,这里得到的是向量而不是矩阵) |
无 |
| tvec | OutputArray | 输出的平移向量 | 使坐标点从世界坐标系平移到相机坐标系 | 无 |
| useExtrinsicGuess | bool | 初始值类型 | 用于 SOLVEPNP_ITERATIVE的参数。 如果为true,初始值可以使用猜测的初始值。 如果为false,使用解析求解的结果作为初始值。 |
false |
| iterationsCount | int | 迭代次数 | 这只是初始值,根据估计外点的概率,可以进一步缩小迭代次数;(此值函数内部是会不断改变的),所以一开始可以赋一个大的值。 | 100 |
| reprojectionError | float | 距离阈值 | Ransac筛选内点和外点的距离阈值,这个根据估计内点的概率和每个点的均方差(假设误差按照高斯分布)可以计算出此阈值。 | 8.0 |
| inliers | OutputArray | 返回内点的序列 | 矩阵形式 | noArray() |
| flags | int | 最小子集的计算模型 | 下面表格细讲 | SOLVEPNP_ITERATIVE |
对于参数flag,有以下几种选择
| 名称 | 含义 | 出处 |
|---|---|---|
| SOLVEPNP_ITERATIVE | 适合点在同一平面上的情况 | |
| SOLVEPNP_P3P | 只适用于3点 | Complete Solution Classification for the Perspective-Three-Point Problem |
| SOLVEPNP_EPNP | 点需要在不同平面 | EPnP: Efficient Perspective-n-Point Camera Pose Estimation |
| SOLVEPNP_DLS | 至少四点不在同一平面 | A Direct Least-Squares (DLS) Method for PnP |
总结一下:
-
对于8个点的情况:EPnP表现良好,DLS表现良好。
-
对于4个点的情况:P3P表现良好,EPnp表现良好,然而P3P实际输入点数为4个,那么最后一个点用于检核。
Epnp在4点的时候表现时好时坏,和控制点的选取状况相关。倘若增加为5个点,则精度有着明显提升
4点的ITERATOR方法取得了很好的效果,甚至比P3P还要好,因为P3P只用三个点参与计算
也就是说,在控制点对数量较少的情况下(4点),只有P3P可以给出正确结果
增加一对控制点(变为5对)之后,Epnp的鲁棒性迅速提升,可以得到正确结果,DLS也同样取得了正确结果。
增加到5对控制点后P3P失效,因为只让用4个点,不多不少。
同样的,5点的ITERATOR方法结果正确。
结论:使用多于4点的EPnP最为稳妥.
空间点融合
经过上面的步骤,我们就可以得到新添加图像的变换矩阵和匹配点的空间坐标。
将其与之前已经计算好的图像空间坐标序列进行融合。
void PointsFusion(vector<int> &pts_indices, vector<int> &next_pts_indices,
vector<Point3d> &pts_3d, vector<Point3d> &next_pts_3d,
vector<Vec3b> &colors, vector<Vec3b> &next_colors)
{
vector<DMatch> matches = allMatches[img_idx];
for(int i = 0; i < matches.size(); i++)
{
int query_idx = matches[i].queryIdx;
int train_idx = matches[i].trainIdx;
int pts_idx = pts_indices[query_idx]; //-- 查找新配对图像点是否存在于空间点索引序列中
if(pts_idx >= 0) //-- 若该点在空间中已经存在,则这对匹配点对应的空间点应该是同一个,索引要相同
{
next_pts_indices[train_idx] = pts_idx;
continue;
}
pts_3d.push_back(next_pts_3d[i]); //-- 该点不存在,说明是新加入图像和上一张图像的匹配点,将其加入到空间点对中
colors.push_back(next_colors[i]);
pts_indices[query_idx] = pts_3d.size() - 1; //-- 设置该匹配点的索引
next_pts_indices[train_idx] = pts_3d.size() - 1;
}
}
这一步的pts_indices和next_pts_indices容易把人搞晕,需要着重强调一下。
从全局来看,我们首先定义了存放所有三维匹配点的数组vector
correspond_pts_idx[i][j]代表第i幅图像第j个特征点所对应的空间点在点云中的索引,若索引小于零,说明该特征点在空间当中没有对应点。通过此结构,由特征匹配中的queryIdx和trainIdx就可以查询某个特征点在空间中的位置。
// -- Init -- //
correspond_pts_idx.clear();
correspond_pts_idx.resize(allKeypoints.size()); //-- 大小初始化为与allKeypoints一致
for(int i = 0; i < allKeypoints.size(); i++)
{
correspond_pts_idx[i].resize(allKeypoints[i].size(), -1); //-- 初始化每幅图的特征点对应索引矩阵,默认值为-1
}
//-- 填写头两幅图像的结构索引
int idx = 0;
vector<DMatch> &matches = allMatches[0];
for(int i = 0; i < matches.size(); i++)
{
if (mask.at<uchar>(i) == 0) continue; //-- 当前关键点为异常值,则跳过
//-- 如果两个点对应的idx 相等 表明它们是同一特征点 idx 就是pts_3d中对应的空间点坐标索引
correspond_pts_idx[0][matches[i].queryIdx] = idx;
correspond_pts_idx[1][matches[i].trainIdx] = idx;
++idx;
}
// -- PointsFusion -- //
// 这里的pts_indices 就是 correspond_pts_idx[k], next_pts_indices就是correspond_pts_idx[k] + 1
for(int i = 0; i < matches.size(); i++)
{
int query_idx = matches[i].queryIdx;
int train_idx = matches[i].trainIdx;
int pts_idx = pts_indices[query_idx]; //-- 查找新配对图像点是否存在于空间点索引序列中
if(pts_idx >= 0) //-- 若该点在空间中已经存在,则这对匹配点对应的空间点应该是同一个,索引要相同
{
next_pts_indices[train_idx] = pts_idx;
continue;
}
pts_3d.push_back(next_pts_3d[i]); //-- 该点不存在,说明是新加入图像和上一张图像的匹配点,将其加入到空间点对中
colors.push_back(next_colors[i]);
pts_indices[query_idx] = pts_3d.size() - 1; //-- 设置该匹配点的索引
next_pts_indices[train_idx] = pts_3d.size() - 1;
}
首先在初始化中,我们把correspond_pts_idx初始化,大小与关键点匹配数(也即图像个数)相等。
对于每一张图像的索引,都初始化大小为该图像匹配点的个数大小。
经过初始化之后,得到了一个二维的”稀疏“矩阵(“稀疏”即为大部分值都为-1)
其中m[0][1] = 0,m[1][0]=0,即第一张图像的keypoints_1[1] 与 keypoints_2[0]相匹配。match[0].queryIdx = 1, matche[0].trainIdx = 0。
之和进行点云融合pts_idx即为第二张图像的queryIdx,如果在原矩阵中值不为-1,则说明该索引作为trianIdx曾经与第一张图像相匹配,是一对匹配点,那么从而新加入的第三张图像与前两张图像有共同的匹配点。则next_pts_indices[train_idx] = pts_idx;
其中x是与之前没有共同匹配点的点对,后面会讲。而m[2][3] = 0,这就说明keypoints_3[3]与keypoints_1[1]与keypoints_2[0]这三个点构成匹配关系。
那么如果第二幅图与第三幅图的匹配点对在第一幅图中不匹配呢?
- 把该点存入整体的三维点序列中
- 类似于Init的初始化前两维一样,初始化第二维和第三维,但idx是从pts_3d.size() - 1开始(因为已经添加了新的点,在索引里为了保持连续性要将个数-1)
理论上,每个大于0的数字,至少出现两次,但是在实际操作中,会有一定的问题。
经过测试,会出现一个数字只出现一次的可能性,那是因为什么呢?
在初始化时,queryIdx对应的trainIdx不会只与这一个queryIdx对应,有可能还会与其他的queryIdx对应,即第二幅图中的一个点能与第一幅图中一个或多个进行匹配。那么第二次匹配时,就会把第一次的结果覆盖掉,导致某个数字只出现了一次。
可以对Init进行修改(其实没有必要)
if(correspond_struct_idx[1][matches[i].trainIdx] == -1)
{
//todo
//-- 当第二个矩阵的元素没有匹配过时,才与第一个元素进行匹配,否则不匹配。
}
导出数据
经过以上步骤,我们就获得了所有图片针对第一幅图(世界坐标系)的变换矩阵和空间三维点,就可以进行三维重建稀疏点云了。
void SaveData(string file_name, vector<Point3d>& pts_3d, vector<Vec3b>& colors)
{
int n = (int)rotations.size();
FileStorage fs(file_name, FileStorage::WRITE);
fs << "Camera Count" << n;
fs << "Point Count" << (int)pts_3d.size();
fs << "Rotations" << "[";
for (size_t i = 1; i < n; ++i)
{
fs << rotations[i];
}
fs << "]";
fs << "Motions" << "[";
for (size_t i = 1; i < n; i++)
{
fs << translations[i];
}
fs << "]";
fs << "Points" << "[";
for (size_t i = 0; i < pts_3d.size(); ++i)
{
fs << pts_3d[i];
}
fs << "]";
fs << "Colors" << "[";
for (size_t i = 0; i < colors.size(); ++i)
{
fs << colors[i];
}
fs << "]";
fs.release();
}
整体流程
int main()
{
// ######################################## //
// sfm整体流程 //
// ######################################## //
//-- 内参矩阵(假设已知)
Mat K = (Mat_<double>(3,3) << 1520.0, 0.0, 302.2,
0.0, 1520.0, 246.87,
0.0, 0.0, 1.0);
vector<Vec3b> colors;
vector<Point3d> pts_3d;
//-- 读取图片 --//
ReadImg();
//-- 提取图片特征 --//
ExtractFeatures(images);
//-- 图片特征匹配 --//
MatchFeatures();
//-- 前两幅图像进行初始化 --//
Init(K, pts_3d, correspond_pts_idx, colors);
//-- 从第三幅图开始 --//
for(int i = 1; i < allMatches.size(); i++)
{
//-- 获得当前图像索引(-1) --//
img_idx = i;
//-- 匹配点三维空间坐标 --//
vector<Point3f> object_points;
//-- 匹配点二维空间坐标 --//
vector<Point2f> image_points;
Mat r, R, t;
//-- 得到三维坐标和二维坐标 --//
Get3d2dPoints(pts_3d, correspond_pts_idx[i], object_points, image_points);
//-- PnP!!! --//
solvePnPRansac(object_points, image_points, K, noArray(), r, t, false);
//-- 转换旋转向量至旋转矩阵 --//
Rodrigues(r, R);
rotations.push_back(R);
translations.push_back(t);
vector<Point2f> p1, p2;
vector<Vec3b> c1, c2;
//-- 得到匹配点
MatchPoints(allKeypoints[i], allKeypoints[i+1], allMatches[i], p1, p2);
MatchColors(allColors[i], allColors[i+1], allMatches[i], c1, c2);
vector<Point3d> next_pts_3d;
//-- 对两幅图进行重建,得到R,t 和 三维点坐标
Reconstruct(K, rotations[i], translations[i], R, t, p1, p2, next_pts_3d);
//-- 将得到数据与之前计算的进行融合
PointsFusion(correspond_pts_idx[i], correspond_pts_idx[i+1], pts_3d, next_pts_3d, colors, c1);
}
//-- 存储数据
SaveData(path + "structure.yml", pts_3d, colors);
}
恢复效果
使用以下四张图进行恢复

效果如下:

几个问题
整个程序其实是很基础的一个sfm演示,没有考虑太多的东西进去,只是把sfm应有的流程走了一遍。
在实际实验时发现了几个问题,暂时还没想到解决的办法。
- 当两张图片偏差角度过大时,相机的位置会错误。

当使用以上两张图片进行重建时,提取的特征点很少很少,从而导致了相机位置发生错误。重建失败。
- 第一张和第二张图片分解的R,t与后面的R,t差距较大
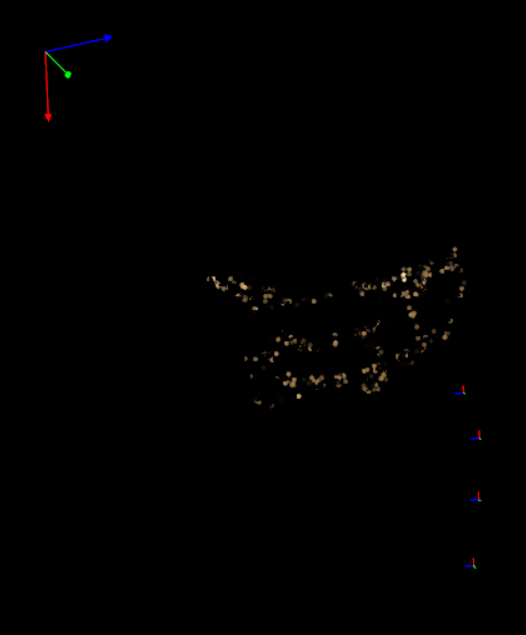
可以看到,左上角的相机为第一张图和第二张图使用基础矩阵恢复出来的R,t。
而其他的摄像机则是使用PnP恢复出的R,t。
可以看到,第一组R,t与后面的R,t差距较大。

原因是第一组R,t是由本质矩阵恢复而来,位移不具有尺度信息。
-
点的深度问题
原因不明。
在侧面看是

而一旦转一个视角

可以看到在z轴(深度)计算上多少还是有点问题的。
手动调一下将所有点的z坐标 / 10

可以看到,z轴基本符合要求。
后续优化
还可以使用BA进行后续优化。有空的时候再进行研究。


