PnP学习笔记（更新ing）

PnP

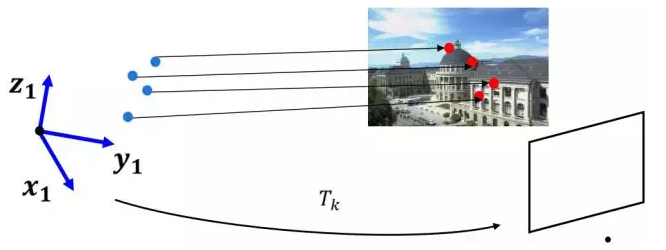
• 给定：一张已知特征点3D位置的图像，一张二维图像。
• 已知：特征点在世界坐标系（指的是相机最初位置的那个坐标系）下的三维坐标，特征点映射到图像上的二维坐标，三维坐标系中的特征点与二维图像上的匹配关系。
• 未知：相机坐标系在世界坐标系下的位姿，特征点在相机坐标系下的深度。
• 最初使用对极几何，初始化出特征点的深度。对于后续的二维图像，当前帧与之前帧进行特征点匹配。匹配到的点若之前已经估计出深度，就知道了世界坐标系下的三维坐标和当前帧二维点的匹配关系，可以用PNP求解当前帧的相机，相对于世界坐标系的位姿变换。

直接线性变换(DLT)

考虑某个空间点P，它的齐次坐标为\(P = (X,Y,Z,1)^T\)。在图像\(I_1\)中，投影找到特征点\(x_1 = (u_1,v_1,1)^T\)（以归一化平面齐次坐标表示）。此时，相机的位姿\(R,t\)是未知的。与单应矩阵的求解类似，我们定义增广矩阵\([R|t]\)为一个\(3 \times 4\)的矩阵，包含了旋转和平移信息。展开形式如下：

\[s \left( \begin{matrix} u_1\\v_1\\1 \end{matrix} \right) = \left( \begin{matrix} t_1 & t_2 & t_3 & t_4\\ t_5 & t_6 & t_7 & t_8\\ t_9 & t_{10} & t_{11} & t_{12}\\ \end{matrix} \right) \left( \begin{matrix} X\\Y\\Z\\1 \end{matrix} \right) \]

用最后一行把s消去，得到两个约束

\[u_1 = \frac{t_1X+t_2Y+t_3Z+t_4}{t_9X+t_{10}Y+t_{11}Z+t_{12}}\\ v_1 = \frac{t_5X+t_6Y+t_7Z+t_8}{t_9X+t_{10}Y+t_{11}Z+t_{12}} \]

定义\(T\)的行向量：

\[t_1 = (t_1,t_2,t_3,t_4)^T\\ t_2 = (t_5,t_6,t_7,t_8)^T\\ t_3 = (t_9,t_{10},t_{11},t_{12})^T \]

于是有

\[t_1^TP - t_3^TPu_1 = 0\\ t_2^TP-t_3Pv_1=0 \]

\(t\)是待求的变量，可以看到，每个特征点提供了两个\(t\)的线性约束。假设一共有\(N\)个特征点，则可以列出如下线性方程组：

\[\left( \begin{matrix} P_1^T & 0 & -u_1P_1^T\\ 0 & P_1^T & -v_1P^T_1\\ \vdots & \vdots & \vdots\\ P_N^T & 0 & -u_NP_N^T\\ 0 & P_N^T & -v_NP_N^T \end{matrix} \right) \left( \begin{matrix} t_1\\t_2\\t_3 \end{matrix} \right)=0 \]

\(t\)一共有12维，因此最少通过6对匹配点即可实现矩阵\(T\)的线性求解，这种方法称为\(DLT\)，当匹配点大于6对时，用\(SVD\)对超定方程求最小二乘数

需要解释的是，这里的\(x_1\)使用了归一化平面坐标，去掉了内参矩阵K的影响——因为内参\(K\)在SLAM中假设为已知，即使内参未知也可以用PnP来估计\(K,R,t\)三个量

P3P

仅利用3对匹配点，对数据要求较少

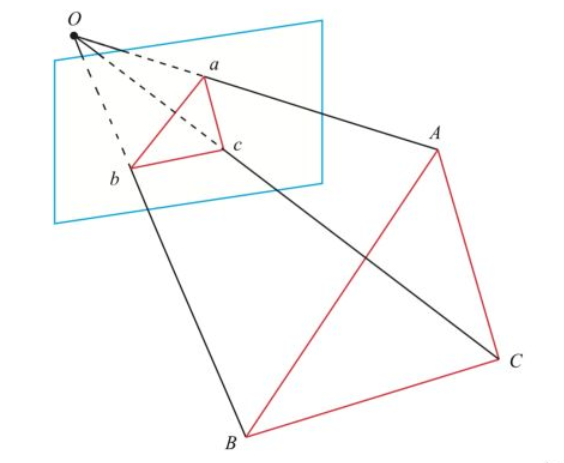
P3P需要利用给定的3个点的几何关系。\(ABC\)为三个世界坐标中的点，\(abc\)为\(ABC\)投影在图像上的点。已知ABC的世界坐标系中的坐标，\(abc\)的相机坐标系坐标。O为相机中心，三角形\(Oac\)和\(OAC\)，\(Oab\)和\(OAB\)，\(Obc\)和\(OBC\)两两相似。

此外，P3P需要使用一对验证点，记验证点对为\(D-d\)

根据余弦定理：

\[OA^2 + OB^2 - 2OA·OB·cos(a,b) = AB^2\\ OB^2 + OC^2 - 2OB·OC·cos(b,c) = BC^2\\ OA^2 + OC^2 - 2OA·OC·cos(a,c) = AC^2 \]

令\(v = \frac{AB^2}{OC^2}\)，\(uv = \frac{BC^2}{OC^2}\)，\(wv = \frac{AC^2}{OC^2}\)，有：

\[x^2 + y^2 - 2xycos(a,b) - v = 0\\ y^2 + 1 - 2ycos(b,c) - uv = 0\\ x^2 + 1 - 2xcos(a,c) - wv = 0 \]

整理得：

\[(1-u)y^2 - ux^2 - cos(b,c)y + 2uxycos(a,b) + 1= 0\\ (1-w)x^2 - wy^2 - cos(a,c)x + 2wxycos(a,b) + 1= 0 \]

其中\(x,y\)未知，也就是\(A,B,C\)在相机坐标系下的坐标\(OA,OB,OC\)的长度未知。

方程最多得到四个解，用于验证点来计算最可能的解，得到\(3D\)坐标。之后可以求解两组\(3D\)坐标系之间的\(R，t\)。

存在的问题：

• 只利用三个点的信息，多于三个点时，难以利用。
• 存在误匹配或噪声，则失效。

Bundle Adjustment

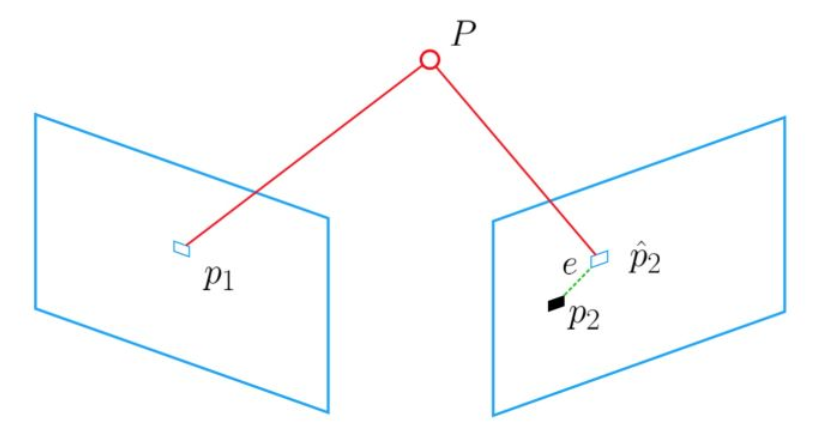
Bundle Adjustment的思想是通过最小化重投影误差，求解位姿。

原本\(P\)的投影点应该是\(P_1\)和\(P_2\) ，但是由于误差的存在，观测到\(P\)在图像2上的投影点是 \(\hat{P_2}\) ，观测值和实际值的误差记为\(e\)。通过调整相机的位姿，来找到\(e\)的最小值，认为使误差最小的位姿就是真实的相机运动。