运动恢复结构(SFM)

运动恢复结构

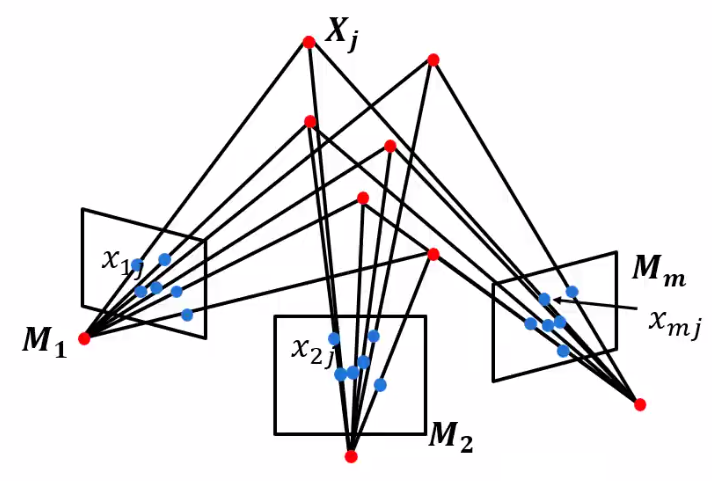
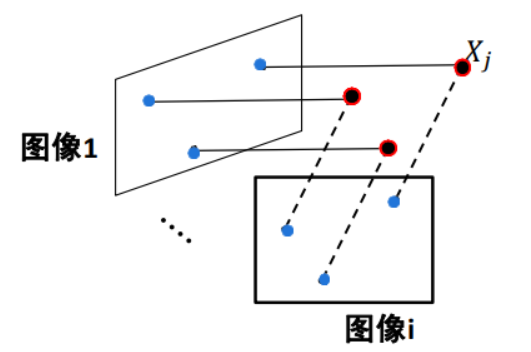
通过三维场景的多张图片，恢复出该场景的三维结构信息以及每张图片对应的摄像机参数。

已知：n个3D点\(X_j\)在m张图像中的对应点的像素坐标\(x_{ij}\)\((i = 1, …, m, j = 1, …, n)\)，且\(x_{ij} = M_iX_j\) \((i = 1,...,m,j=1,...,n)\)

其中，\(M_i\)是第i张图片对应的摄像机的投影矩阵

求解：

• m个摄像机投影矩阵\(M_i\)\((i = 1, … , m)\) \(\longrightarrow\) 运动(motion)
• n个三维点\(X_j(j=1,...,n)\)的坐标 \(\longrightarrow\) 结构(structure)

三种典型的运动恢复结构问题

• 欧式结构恢复（摄像机内参数已知，外参数未知）
• 仿射结构恢复（摄像机为仿射相机，内、外参数均未知）
• 透视结构恢复（摄像机为透视相机，内、外参数均未知）

欧式结构恢复

已知：

• n个三维点\(X_j(j = 1, ..., n)\)在\(m\)张图像中的对应点的像素坐标\(x_{ij}\)

• m张图像对应的摄像机内参数矩阵\(K_i(i=1,...,m)\)

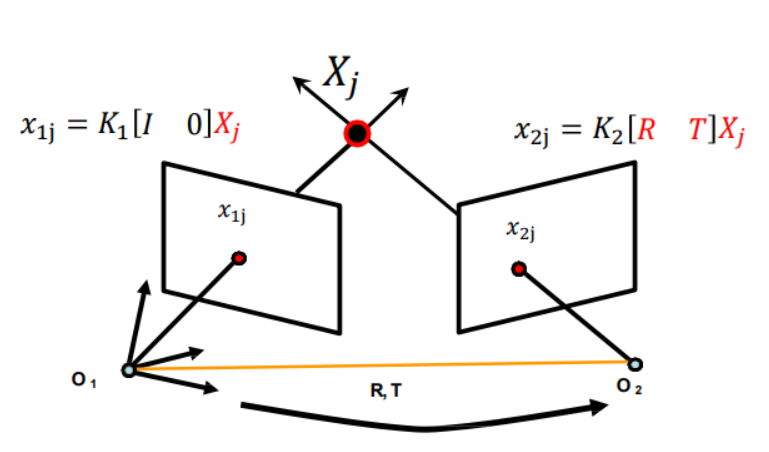
  且 \(x_{ij} = M_iX_j = K_i[R_i\quad T_i]X_j \qquad i = 1,..., m; j = 1, ..., n\)

  其中\(m\)为图像个数，\(n\)为3D点个数，\(M_i,K_i,[R_i\quad T_i]\)为第\(i\)张照片对应的摄像机的投影矩阵、内参数及外参数矩阵

求解

• n个三维点\(X_j(j = 1,...,n)\)的坐标
• m个摄像机外参数\(R_i\)以及\(T_i\)\((i=1,...,m)\)

问题：(2视图)

\[x_{1j} = M_1X_j = K_1[I \quad 0]X_j\\ x_{2j} = M_2X_j = K_2[R \quad T]X_j \]

求解：

1. 求解基础矩阵F

   归一化八点法

   点的对应关系：左图和右图进行sift特征提取，对每一个特征点进行描述，建立两张图的特征点的对应关系。用RANSAC的方法去估计正确的变换矩阵从而剔除错误点。

   1、SIFT 2、匹配 3、RANSAC

   如果正好8对点，则只有唯一解，多于8对点则使用最小二乘求解

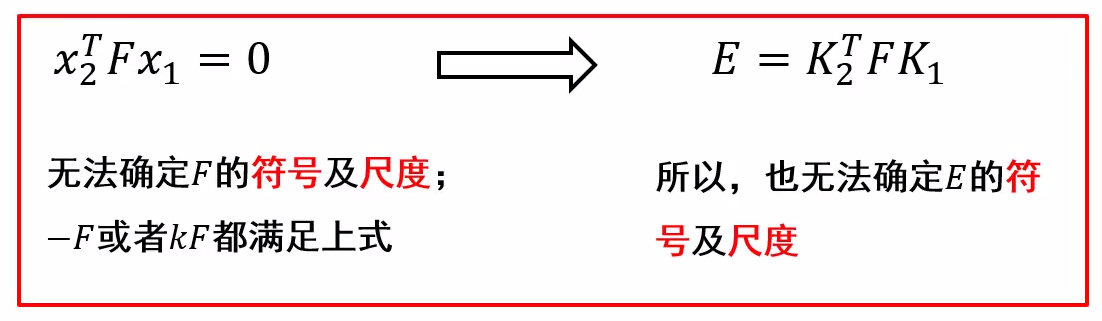
2. 利用F与摄像机内参数求解本质矩阵E

   \(E = K_2^TFK_1\)

3. 分解本质矩阵获得R与T

   \(E \longrightarrow R、T \longrightarrow M_2\)

4. 三角化求解三维点\(X_j\)坐标

   \(X_j^* = \mathop{argmin}\limits_{X_j}(d(x_{1j},M_1X_j) + d(x_{2j},M_2X_j))\)

本质矩阵分解

\[E = [T_{\times}]R \]

找到一个策略把E因式分解成两部分

重要说明：

定义两个矩阵：

\[Z = \left[ \begin{matrix} 0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 0 \end{matrix} \right] \qquad W = \left[ \begin{matrix} 0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1 \end{matrix} \right] \]

重要性质：

在相差一个正负号的情况下

\[Z = diag(1,1,0)W = diag(1,1,0)W^T \]

\([T_{\times}]\)可以写成：\([T_{\times}] = kUZU^T\)，其中\(U\)是单位正交阵，k是常数

不考虑符号、尺度，则

\[\begin{eqnarray} [T_{\times}] &=& UZU^T\\ &=& Udiag(1,1,0)WU^T\\ &=& Udiag(1,1,0)W^TU^T（可能）\\ &=& Udiag(1,1,0)W^TU^T（也可能） \end{eqnarray}\\ \]

所以

\[\begin{eqnarray} E &=& [T_{\times}]R = (Udiag(1,1,0)WU^T)R\\ &=& Udiag(1,1,0)(WU^TR) \end{eqnarray} \]

同时，对E进行奇异值分解

\[E = U diag(1,1,0)V^T \]

与上面的进行比较，发现可以把R表示出来

\[V^T = WU^TR \longrightarrow R = UW^TV^T\quad or\quad R = UWV^T \]

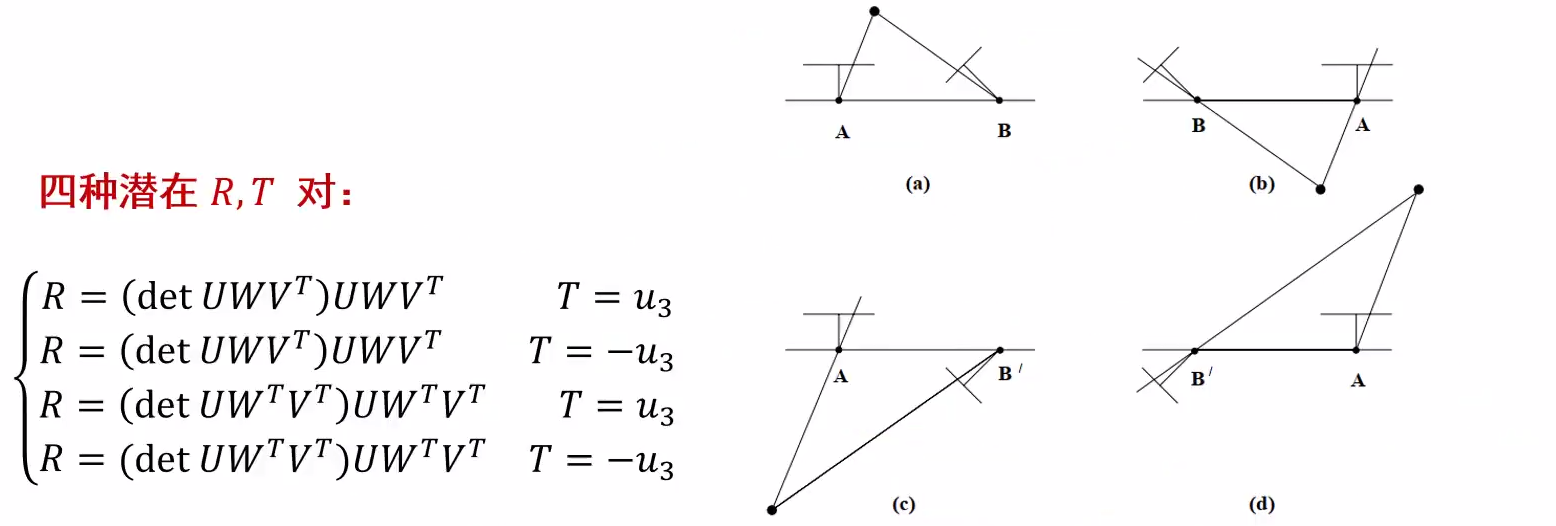
注意：E的这个因式分解只保证了矩阵\(UWV^T\)或\(UW^TV^T\)是正交的。其为旋转矩阵还需确保行列式的值为正：

\[R = (detUWV^T)UWV^T \quad or \quad (detUW^TV^T)UW^TV^T \]

这样R就为正，即为真正的旋转矩阵

而怎么求解T呢？

由前面的\([T_{\times}] = UZU^T\)可以得到\(T \times T = [T_{\times}]T = UZU^TT = 0\)，从而\(T = \pm u_3\)（U的第三列）

这里其实是相当于\(AT = 0\)，即\(T\)为\(A\)最小特征值对应的特征向量，而\(A\)本质上是SVD分解得到的\(UZU^T\)，所以T就是\(U^T\)的最小特征值的特征向量，即为U的第三列

• 选择一个点三角化，正确的一组解能保证该点在两个摄像机的z坐标均为正
• 对多个点进行三角化，选择在两个摄像机系下z坐标均为正的个数最多的那组R、T。（更鲁棒）

做一个总结：

欧式结构恢复出的解没有尺度概念，需要其他先验信息！

• 仅靠图像去重建的三维场景与真实场景相差一个相似变换（旋转、平移、缩放）
• 恢复的场景与真实场景之间仅存在相似变换的重构称为度量重构

仿射结构恢复

问题：已知n个三维点\(X_j\)在m张图像中的对应点的像素坐标\(x_{ij}\)\((i = 1, …, m, j = 1, …, n)\)，且\(x_{ij} = A_iX_j+b_i\) \((i = 1,...,m,j=1,...,n)\)

​ 其中，\(A_i,b_i\)组成了第i张图片对应的仿射摄像机的投影矩阵$M_i = \left[\begin{matrix}A_i & b_i \ 0 & 1\end{matrix}\right] $

求解：

• n个三维点\(X_j(j = 1,...,n)的坐标\)
• m个仿射摄像机的投影矩阵\(A_i\)与\(b_i(i=1,...,m)\)

方法：

• 代数方法
• 因式分解法
  • 数据中心化
  • 因式分解

中心化：减去图像点的质心

i表示第i个摄像机，\(x_{ij}\)表示第i个摄像机的第j个点

\[\hat{x}_{i,j} = x_{ij} - \overline{x}_i\qquad\overline{x}_i = \frac{1}{n}\sum\limits_{k=1}^n x_{ik} \qquad x_{ij} = A_iX_j + b_i \]

于是

\[\begin{eqnarray} \hat{x}_{ij} = x_{ij} - \frac{1}{n}\sum\limits_{k=1}^nx_{ik} &=& A_iX_j + b_i - \frac{1}{n}\sum\limits_{k=1}^nA_iX_k - \frac{1}{n}\sum\limits_{k=1}^nb_i\\ &=&A_i(x_j-\frac{1}{n}\sum\limits_{k=1}^nX_k) = A_i(X_j-\overline{X} = A_i\hat{X}_j) \end{eqnarray} \]

如果3D点的质心 = 世界坐标系的中心，则\(\hat{x}_{ij} = A_i\hat{X}_j = A_iX_j\)

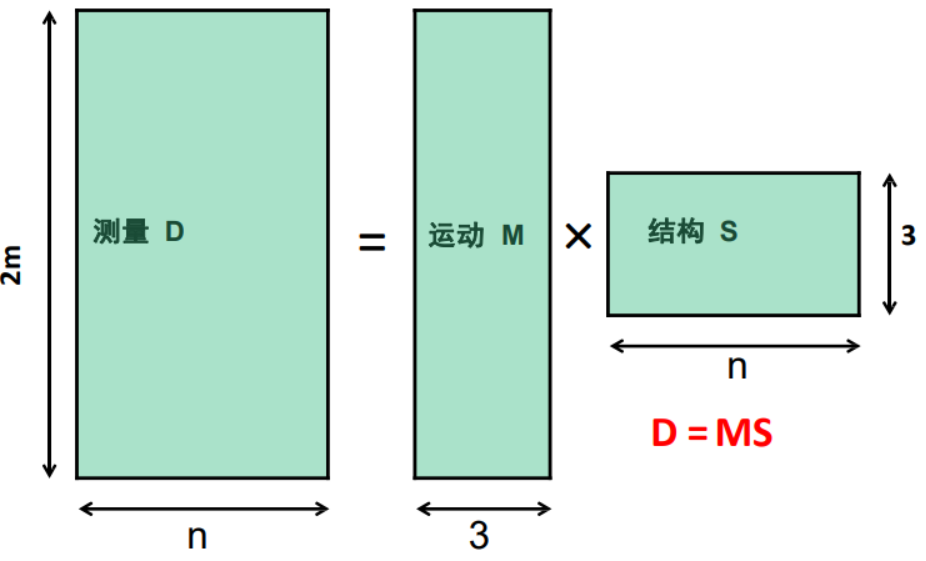
因式分解

把取均值后的\(m \times n\)个测量值写成矩阵的形式：

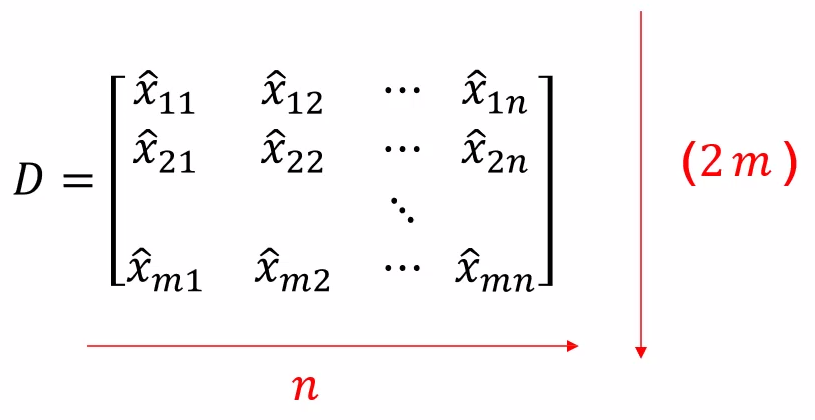
\(\left[\begin{matrix}x_{11} & x_{12} & \dots & x_{1n}\end{matrix}\right]^T\)是第一个相机下的点，每个\(x_{ij}\)是一个\(2 \times 1\)的向量，为\([u\quad v]^T\)，所以\(\hat{x}_{11} = [\overline{u}\quad \overline{v}]^T\)

怎么分解D呢？

通过计算D的奇异值分解

由于\(rank(D) = 3\)，理想情况下这里只有三个非零的奇异值\(\sigma_1,\sigma_2,\sigma_3\)

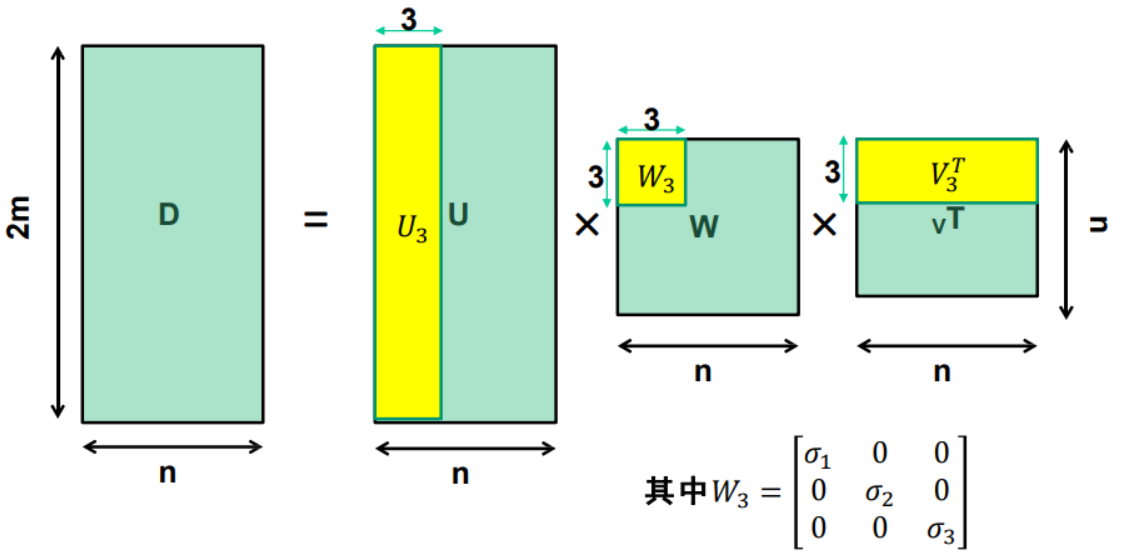
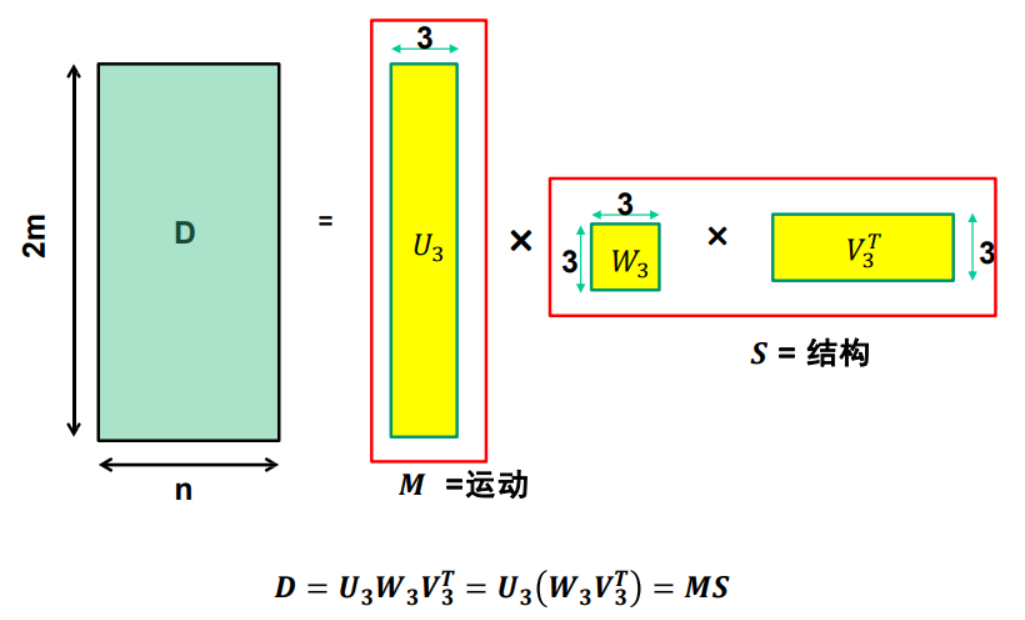
总结：

问题：这样分解可以吗？\(\longrightarrow\)可以。因此，解不是唯一的

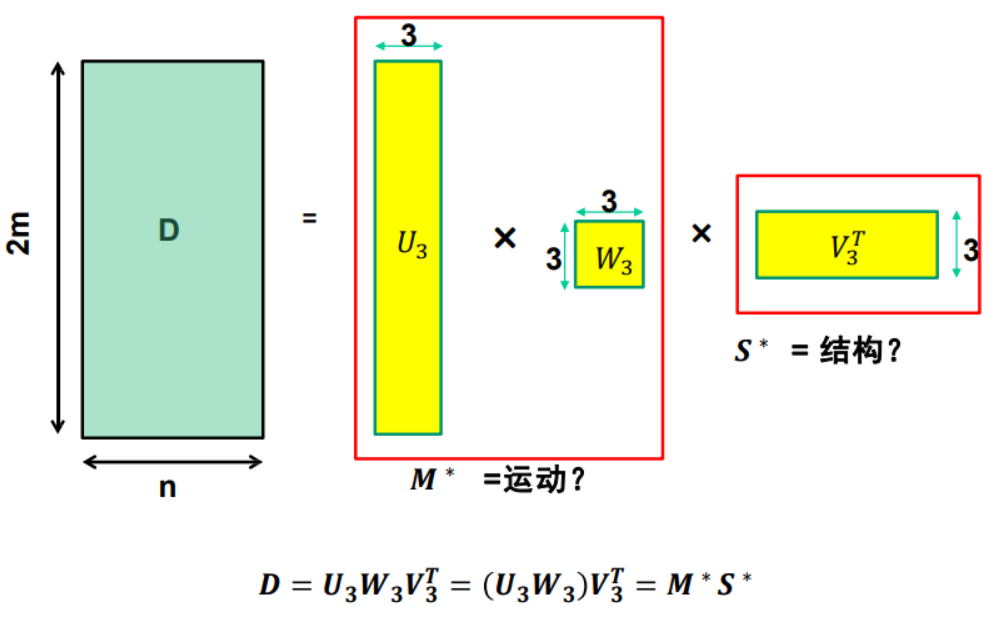
仿射结构恢复歧义：

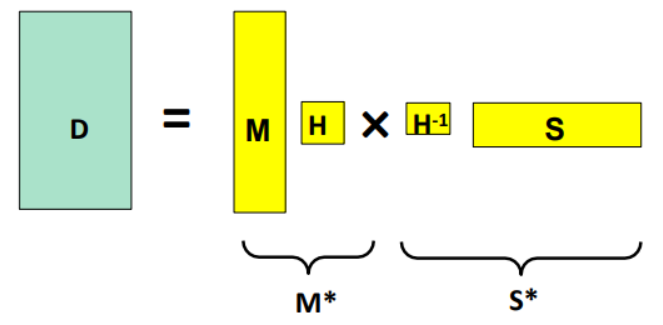
• 分解不唯一。通过以下变换可以得到相同的D：

  \[M^* = MH\\ S^* = H^{-1}S \]

  其中\(H\)是任意可逆的\(3\times 3\)矩阵

• 必须利用其他约束条件来解决歧义

问题：给定m个相机，n个三维点，可以有多少个等式\((2mn)\)，多少个未知量\((3n+8m - 8)\)?

由于求不出真实解，与真实解总相差一个H矩阵\((3 \times 3)\)，这个矩阵有8个自由度，所以真正有解的是\(3n + 8m - 8\)，要把8减去

即需要约束 \(2 m n \ge 3n + 8m - 8\)

透视结构恢复

问题：已知n个三维点\(X_j(j = 1,...,n)\)在m张图像中的对应点的像素坐标\(x_{ij}\)，且\(x_{ij} = M_iX_j,(i = 1,...,m;j = 1,...,n)\)

​ 其中，\(M_i\)为第\(i\)张图片对应的摄像机的投影矩阵

求解：

• n个三维点\(X_j(j=1,...,n)\)的坐标
• m个摄像机投影矩阵\(M_i(i = 1,...,m)\)

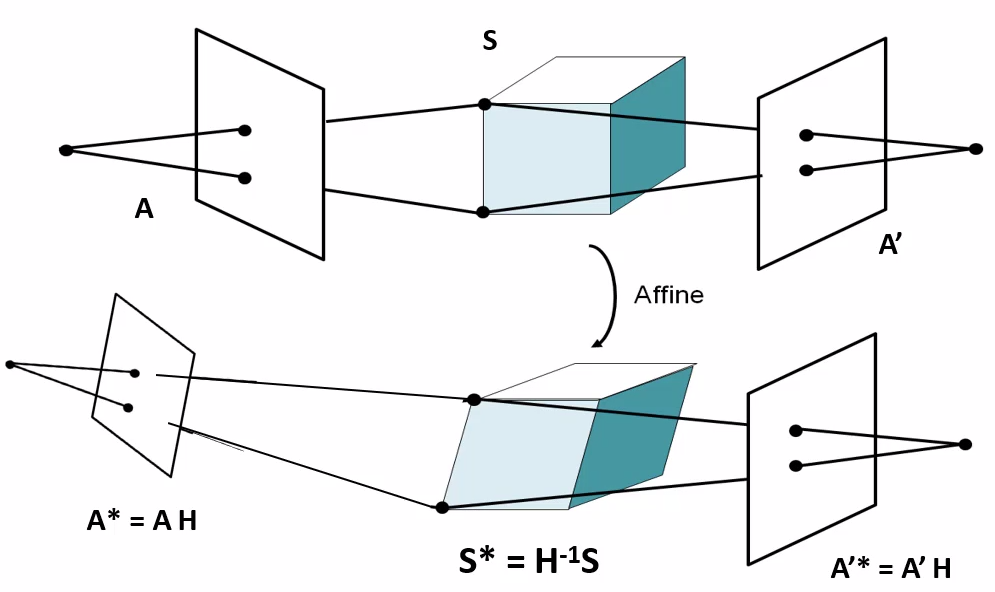
以两视图为例：

\[x_{ij} = M_iX_j \qquad\qquad M_i = K_i[R_i\quad T_i] \]

式子乘一个\(H\)和\(H^{-1}\)得

\[x_{ij} = M_iX_j = (M_iH^{-1})(HX_j) = M^*X^* \]

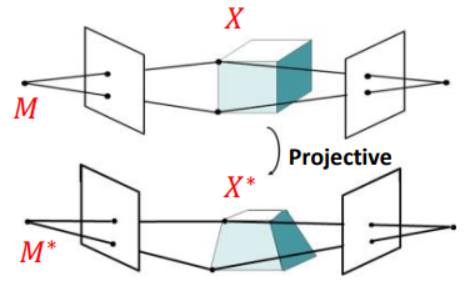
因此\(M、X\) 和 \(M^*、X^*\)都是\(x_{ij}=M_iX_j\)的解(透视结构也有歧义性)

恢复方法：

在相差一个\(4\times 4\)的可逆变换的情况下恢复摄像机运动与场景结构

• 代数方法（通过基础矩阵）
• 因式分解法（通过SVD）
• 捆绑调整

代数方法

1. 求解基础矩阵F

   归一化八点法

2. 利用F估计摄像机矩阵

   \(F \longrightarrow M_1,M_2\)

3. 三角化计算三维点坐标

   \(x_j^* = \mathop{argmin}\limits_{X_j}(d(x_{1j},M_1X_j) + d(x_{2j},M_2X_j))\)

利用F估计摄像机矩阵：

由于透视歧义的存在，我们总是可以找到一个可逆矩阵H，使得：

\[M_1H^{-1} = [I|0] \qquad \qquad M_2H^{-1} = [A|b] \]

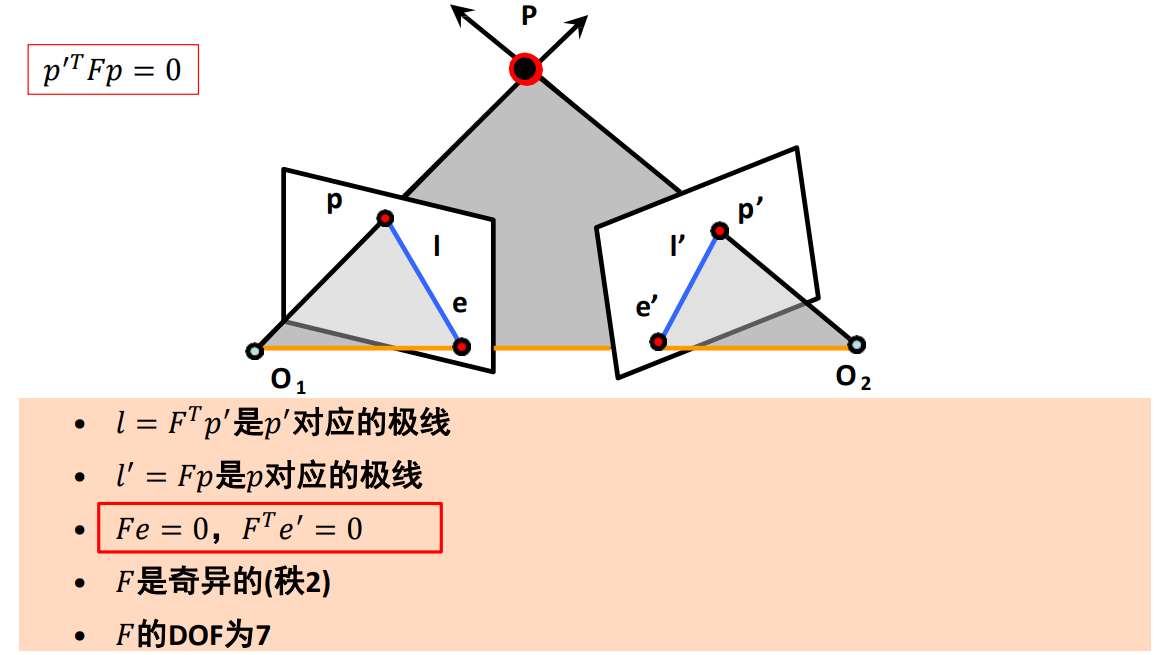
已知：\(x'Fx = 0 \qquad \qquad F = [b_{\times}]A\)

1. 计算b ：

   • 考虑乘积\(F^T b\) \(F^{T}·b = ([b_{\times}]A)^T·b = A^T[b_{\times}]^T·b = -A^T[b_{\times}]·b = 0\) \(F^T b = 0\)

   • b为\(F^T\)矩阵最小奇异值的右奇异向量，且\(||b|| = 1\)

2. 计算A：

   • 定义：\(A' = -[b_{\times}]F\)

   • 验证\([b_{\times}]A' = F\)

     \[[b_{\times}]A' = -[b_{\times}][b_{\times}]F = - (bb^T-|b|^2I)F = -bb^TF + |b|^2F = 0 + 1·F = F \]

   • 因此，\(A = A' = -[b_{\times}]F\)

摄像机矩阵

\[\widetilde{M}_1 = [I \quad 0] \qquad\qquad \widetilde{M}_2 = [-[b_{\times}]F \quad b] \]

那么，这里的b是什么呢？在极几何约束中，有\(F^Te = 0\)这条性质，所以b是一个极点！

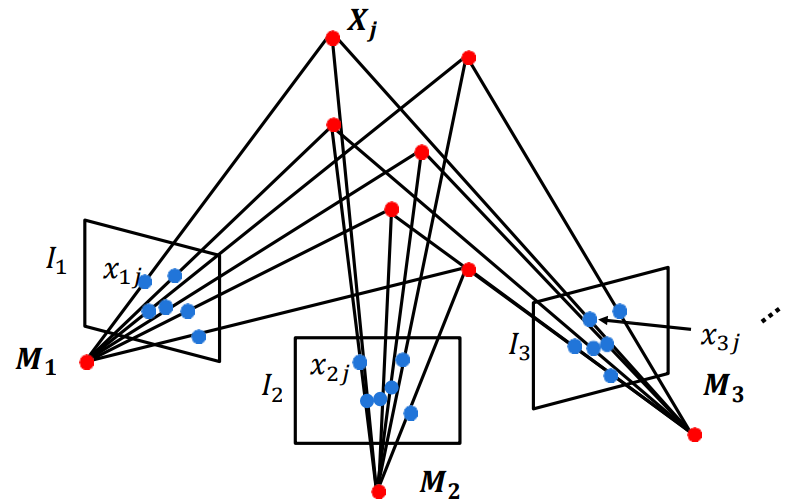
N视图情况：

分别对每一个图像对\(I_k\)和\(I_h\)计算运动与结构

\[I_k，I_h \longrightarrow \widetilde{M}_k，\widetilde{M}_h，\widetilde{X}_{[k,h]} \]

问题：

但是通过两两的方法（从第三个转到第二个再转到第一个）会有累计误差！

捆绑调整（BA)

代数法与分解法的局限性：

• 因式分解法假定所有的点都是可见的，所有下述场合不可用：

  • 存在遮挡
  • 建立对应点关系失败

• 代数法应用于2视图重建

  • 容易出现误差累计

恢复结构和运动的非线性方法

最小化重投影误差：\(E(M,X) = \frac{1}{mn} \sum\limits_{i=1}^m \sum\limits_{j=1}^nD(X_{ij}, M_iX_j)^2\)

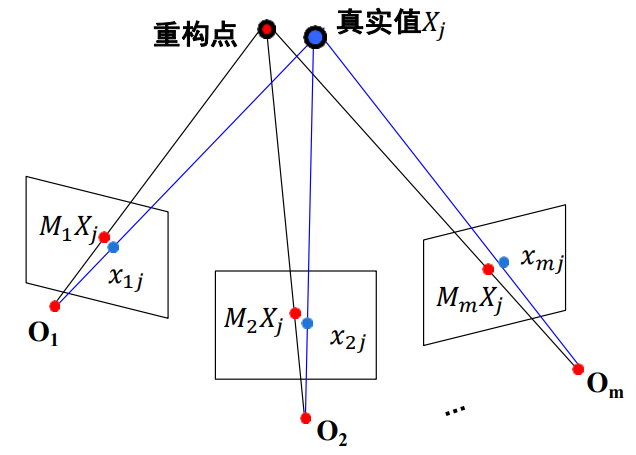
非线性最小化问题：

牛顿法 与 L-M方法 求解

优势：

• 同时处理大量视图
• 处理丢失的数据

局限性：

• 大量参数的最小化问题
• 需要良好的初始条件

实际操作：

• 常用于SFM的最后一步，分解或代数方法可作为优化问题的初始解