Harris角点

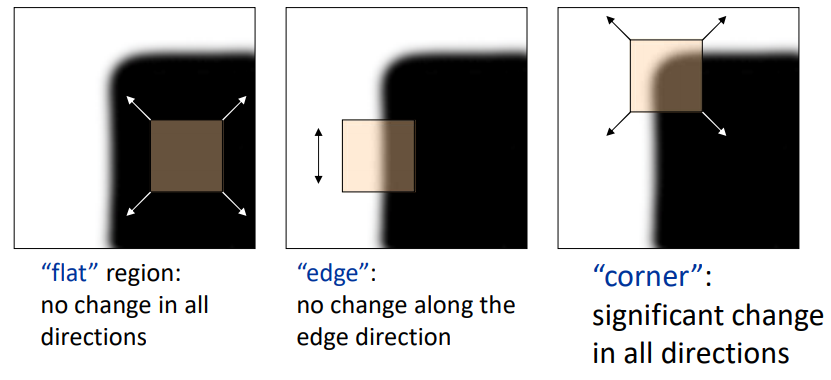
角点：

通常意义上来说，**角点就是极值点，即在某方面属性特别突出的点，是在某些属性上强度最大或者最小的孤立点、线段的终点。更简单来说，有两个方向有变化的点叫做角点。

关于角点的具体描述如下：

一阶导数(即灰度的梯度)的局部最大所对应的像素点；
两条及两条以上边缘的交点；
图像中梯度值和梯度方向的变化速率都很高的点；
角点处的一阶导数最大，二阶导数为零，指示物体边缘变化不连续的方向。

如何识别角点？

使用一个固定窗口（取某个像素的一个邻域窗口）在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，窗口中的像素灰度变化程度，如果存在任意方向上的滑动，都有着较大灰度变化，那么我们可以认为该窗口中存在角点。

数学描述：

公式：

\[E(u,v) = \sum\limits_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2 \]

参数解释：

$[u,v]$是窗口$W$的偏移量
$(x,y)$是窗口$W$所对应的像素坐标位置，窗口有多大，就有多少个位置
$I(x,y)$是像素坐标位置$(x,y)$的图像灰度值
$I(x+u,y+v)$是像素坐标位置$(x+u,y+v)$的图像灰度值
$w(x,y)$是窗口函数，评估每个点的差异值对总能量的贡献

通过分析$(u,v)$和$E(u,v)$的关系分析当前点是否为角点。

如何让$(u,v)$和$E(u,v)$建立直接的联系呢？$\longrightarrow$泰勒展开式

\[E(u,v) \approx E(0,0) + [u,v] \left[ \begin{matrix} E_u(0,0)\\ E_v(0,0) \end{matrix} \right] +\frac{1}{2}[u,v] \left[ \begin{matrix} E_{uu}(0,0) & E_{uv}(0,0)\\ E_{uv}(0,0) & E_{vv}(0,0) \end{matrix} \right] \left[ \begin{matrix} u\\v \end{matrix} \right] \]

\[E_u(u,v) = \sum\limits_{x,y}2w(x,y)[I(x+u, y+v)-I(x,y)]I_x(x+u,y+v)\\ E_{uu}(u,v) = \sum\limits_{x,y}2w(x,y)I_x(x+u,y+v)I_x(x+u,y+v)+\sum\limits_{x,y}2w(x,y)[I(x+u,y+v)-I(x,y)]I_{xx}(x+u,y+v)\\ E_{uv}(u,v) = \sum\limits_{x,y}2w(x,y)I_y(x+u,y+v)I_x(x+u,y+v)+\sum\limits_{x,y}2w(x,y)[I(x+u,y+v)-I(x,y)]I_{xy}(x+u,y+v) \]

\[E(0,0) = 0 \qquad E_u(0,0) = 0 \qquad E_v(0,0) = 0\\ E_{uu}(0,0) = \sum\limits_{x,y}2w(x,y)I_x(x,y)I_x(x,y)\\ E_{uv}(0,0) = \sum\limits_{x,y}2w(x,y)I_y(x,y)I_x(x,y)\\ E_{vv}(0,0) = \sum\limits_{x,y}2w(x,y)I_y(x,y)I_y(x,y) \]

因此：

\[E(u,v) \approx [u,v]M \left[ \begin{matrix} u\\v \end{matrix} \right]\\ M = \sum\limits_{x,y}w(x,y)\left[ \begin{matrix} I_x^2 & I_xI_y\\ I_xI_y & I_y^2 \end{matrix} \right] \]

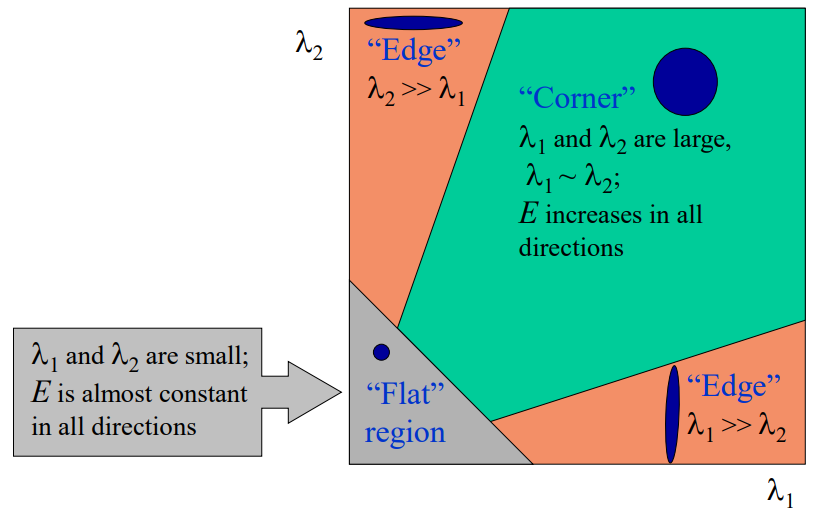
最终可得$M$是$2 \times 2$的矩阵，M矩阵决定了$u,v$对$E(u,v)$的影响，因此分析$M$即可分析$E(u,v)$的特性

假设$I_xI_y$互不影响，即移动是水平垂直的（无旋转）

\[M = \sum\limits_{x,y}w(x,y)\left[ \begin{matrix} I_x^2 & I_xI_y\\ I_xI_y & I_y^2 \end{matrix} \right] = \left[ \begin{matrix} \lambda_1 & 0\\ 0 & \lambda_2 \end{matrix} \right] \]

$$ M = \sum\limits_{x,y}w(x,y)\left[ \begin{matrix} I_x^2 & 0\\ 0 & 0 \end{matrix} \right] \\ E(u,v) = u^2 I_x^2 $$ 所以如果点是边缘点或普通点，则$E(u,v)$最多只与$u$或$v$有关，只有点是角点，$E(u,v)$才与$u,v$都有关

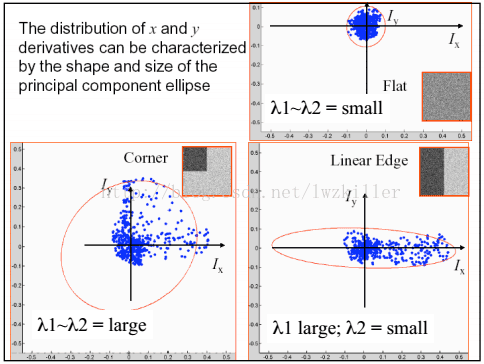
将角点问题转换成求M矩阵的特征值的问题：如果特征值都不等于0，则一定是角点！

$E(u,v) \longrightarrow taylor \longrightarrow M \longrightarrow \lambda_1,\lambda_2$

代入式子后，图像可表示为一个正椭圆$E(u,v) = \frac{u^2}{\frac{1}{\lambda_1}} + \frac{v^2}{\frac{1}{\lambda_2}}$

如果是一个带有旋转的椭圆

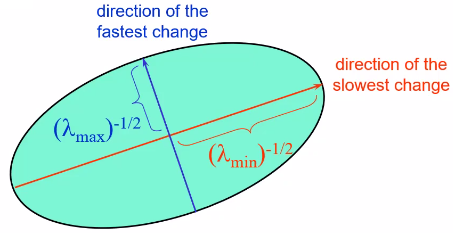
即$M = \left[\begin{matrix}a & b \\ c & d\end{matrix}\right]$（不是水平垂直的，有旋转)，则M一定为实对称矩阵，可以进行分解(R是正交的，可以认为是旋转矩阵)

\[M = R^{-1} \left[ \begin{matrix} \lambda_1 & 0\\ 0 & \lambda_2 \end{matrix} \right] R \]

几何意义来看

由于旋转矩阵$R^{-1} = R^T$，那么

\[[u\quad v]R^T \left[\begin{matrix}\lambda_1 & 0\\0 & \lambda_2\end{matrix}\right]R\left[\begin{matrix}u\\v\end{matrix}\right] = (R\left[\begin{matrix}u\\v\end{matrix}\right])^T \left[\begin{matrix}\lambda_1 & 0\\0 & \lambda_2\end{matrix}\right]R\left[\begin{matrix}u\\v\end{matrix}\right] \]

这样就可以变成正常的$\left[\begin{matrix} \lambda_1 & 0\\ 0 & \lambda_2 \end{matrix} \right]$的形式了

M矩阵的变量和最终获得信息之间的关系：

$\sqrt\lambda_1、\sqrt\lambda_2$为椭圆的长短轴，$R$是椭圆的旋转矩阵（将椭圆转成正的），短轴方向是变化激烈的方向，长轴方向是变化缓慢的方向

因此最终的情况变成：

如何进行简化计算呢？将计算$\lambda$改为计算R

步骤：

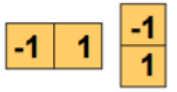
计算每个像素的x,y方向的偏导$I_x,I_y$

\[I_x = \frac{\partial I}{\partial x} = I \otimes (-1\quad 0\quad 1)\\ I_y = \frac{\partial I}{\partial y} = I \otimes (-1\quad 0\quad 1)^T \]
计算每个点的二阶矩矩阵

\[M = R^{-1} \left[ \begin{matrix} \lambda_1 & 0\\ 0 & \lambda_2 \end{matrix} \right] R \]
计算R值

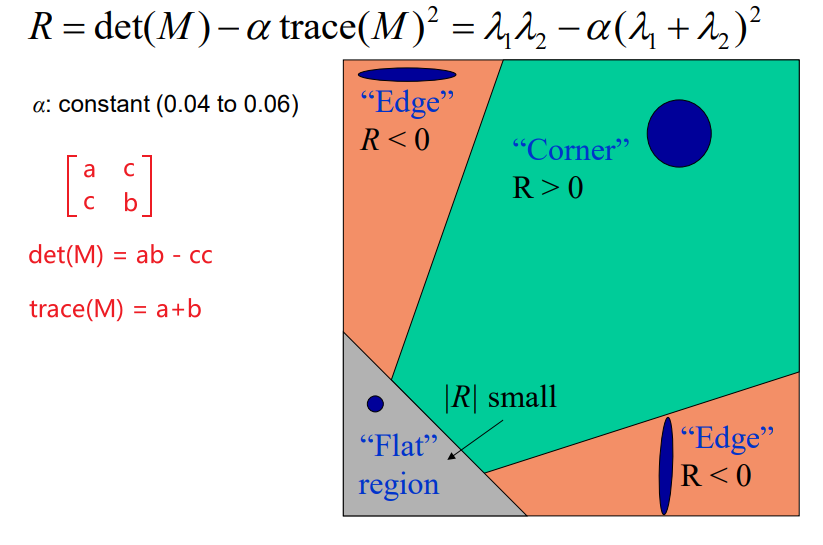
\[R = det(M) - \alpha trace(M)^2 = \lambda_1\lambda_2 - \alpha(\lambda_1 + \lambda_2)^2 \]
当R大于门限时，认为是可能的角点
非最大化抑制

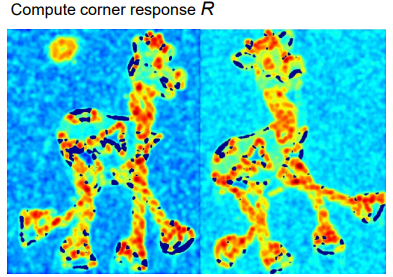
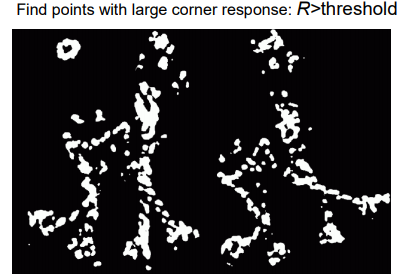
性质：

参数k对角点检测的影响

假设已经得到了矩阵$M$的特征值$\lambda_1 \ge \lambda_2 \ge 0$，令$\lambda_2 = k \lambda_1，0 \le \alpha \le 1$，则

\[R = \lambda_1 \lambda_2 - \alpha(\lambda_1 + \lambda_2)^2 = \lambda_1(k - \alpha(1+k)^2) \]
假设$R \ge 0$，则有

\[0 \le \alpha \le \frac{k}{(1+k)^2} \le 0.25 \]
对于较小的$k$值，$R \approx \lambda_1(k - \alpha),k < \alpha$

由此，可以得出这样的结论，增大$\alpha$的值，降低角点检测的灵敏度，减少被检测角点的数量；减少$\alpha$值，增加角点检测的灵敏度，增加被检测角点的数量。
Harris角点检测算子对亮度和对比度的变化不灵敏

这是因为在进行Harris角点检测时，使用了微分算子对图像进行微分运算，而微分运算对图像密度的拉升或收缩和对亮度的抬高或下降不敏感。换言之，对亮度和对比度的仿射变换并不改变Harris响应的极值点出现的位置，但是，由于阈值的选择，可能会影响角点检测的数量。

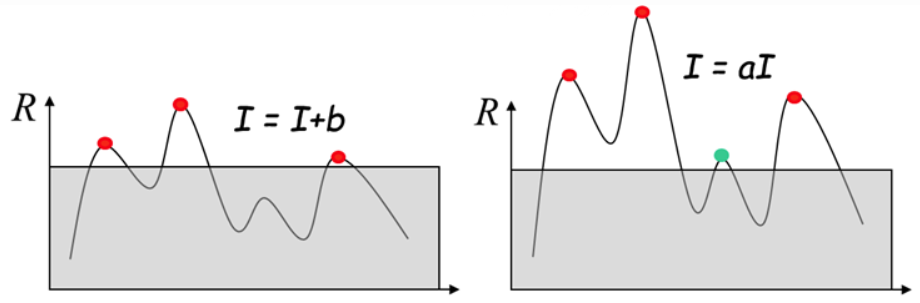
左图表示亮度变化，右图表示对比度变化

Harris角点检测算子具有旋转不变性

Harris角点检测算子使用的是角点附近的区域灰度二阶矩矩阵。而二阶矩矩阵可以表示成一个椭圆，椭圆的长短轴正是二阶矩矩阵特征值平方根的倒数。当特征椭圆转动时，特征值并不发生变化，所以判断角点响应值RR也不发生变化，由此说明Harris角点检测算子具有旋转不变性。
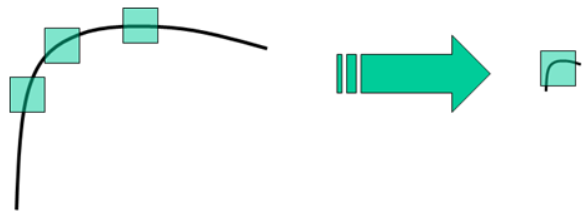
Harris角点检测算子不具有尺度不变性

当图像被缩小时，在检测窗口尺寸不变的前提下，在窗口内所包含图像的内容是完全不同的。左侧的图像可能被检测为边缘或曲线，而右侧的图像则可能被检测为一个角点。

代码实现

主要函数cornerHarris

void cornerHarris(InputArray src, OutputArray dst, int blockSize, int ksize, double k, int borderType=BORDER_DEFAULT)

参数：

src：输入的图像（灰度图）
dst：函数调用后的运算结果存在这里，即这个参数用于存放Harris角点检测的输出结果，和源图片有一样的尺寸和类型。
blockSize：邻域大小
ksize：sobel求取微分时的窗口大小
k：Harris 角点检测方程中的自由参数,取值参数为 [0.04,0.06]

完整程序

#include "opencv2/highgui.hpp"
#include "opencv2/imgproc.hpp"
#include <iostream>
using namespace cv;
using namespace std;
Mat src, src_gray;
int thresh = 100;
int max_thresh = 255;
const char* source_window = "Source image";
const char* corners_window = "Corners detected";
void cornerHarris_demo( int, void* );
int main( int argc, char** argv )
{
    src = imread("qipan.jpg",CV_LOAD_IMAGE_COLOR); 
    if ( src.empty() )
    {
        cout << "Could not open or find the image!\n" << endl;
        return -1;
    }
    cvtColor( src, src_gray, COLOR_BGR2GRAY ); //把图像转换为灰度图
    namedWindow( source_window );
    createTrackbar( "Threshold: ", source_window, &thresh, max_thresh, cornerHarris_demo ); //创建一个调整阈值的工具条
    imshow( source_window, src );
    cornerHarris_demo( 0, 0 ); 
    waitKey();
    return 0;
}
void cornerHarris_demo( int, void* )
{
    int blockSize = 2;
    int apertureSize = 3;
    double k = 0.04;
    Mat dst = Mat::zeros( src.size(), CV_32FC1 );
    
    //角点检测
    cornerHarris( src_gray, dst, blockSize, apertureSize, k );
    
    //归一化
    Mat dst_norm, dst_norm_scaled;
    normalize( dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat() );
    convertScaleAbs( dst_norm, dst_norm_scaled );
    
    //用圆标出角点
    for( int i = 0; i < dst_norm.rows ; i++ )
    {
        for( int j = 0; j < dst_norm.cols; j++ )
        {
            if( (int) dst_norm.at<float>(i,j) > thresh )
            {
                circle( dst_norm_scaled, Point(j,i), 5,  Scalar(0), 2, 8, 0 );
            }
        }
    }
    namedWindow( corners_window );
    imshow( corners_window, dst_norm_scaled );
}

源码剖析:

源码路径： …opencv\sources\modules\imgproc\src\corner.cpp

Mat src = _src.getMat();
_dst.create( src.size(), CV_32FC1 );
Mat dst = _dst.getMat();
cornerEigenValsVecs( src, dst, blockSize, ksize, HARRIS, k, borderType );

可见cornerHarris内部调用了cornerEigenValsVecs函数

static void
cornerEigenValsVecs( const Mat& src, Mat& eigenv, int block_size,
                     int aperture_size, int op_type, double k=0.,
                     int borderType=BORDER_DEFAULT )

参数与上面的cornerHarris类似，就不多解释了

该函数内部先利用sobel算子求水平方向和竖直方向的微分

Mat Dx, Dy;
if( aperture_size > 0 )
{
    Sobel( src, Dx, CV_32F, 1, 0, aperture_size, scale, 0, borderType );
    Sobel( src, Dy, CV_32F, 0, 1, aperture_size, scale, 0, borderType );
}
else
{
    Scharr( src, Dx, CV_32F, 1, 0, scale, 0, borderType );
    Scharr( src, Dy, CV_32F, 0, 1, scale, 0, borderType );
}

然后初始化协方差矩阵cov（三通道，依次保存$dx\times dx, dx\times dy, dy\times dy$）

for( ; j < size.width; j++ )
{
    float dx = dxdata[j];
    float dy = dydata[j];

    cov_data[j*3] = dx*dx;
    cov_data[j*3+1] = dx*dy;
    cov_data[j*3+2] = dy*dy;
}

接下来对协方差矩阵进行在前述设定窗口内进行均值（盒式）滤波：

boxFilter(cov, cov, cov.depth(), Size(block_size, block_size),Point(-1,-1), false, borderType );

if( op_type == MINEIGENVAL )
    calcMinEigenVal( cov, eigenv );
else if( op_type == HARRIS )
    calcHarris( cov, eigenv, k );
else if( op_type == EIGENVALSVECS )
    calcEigenValsVecs( cov, eigenv );

利用滤波后的协方差矩阵求取特征值和特征向量，根据设定不同的op_type调用不同的函数计算，以EIGENVALSVECS为例，调用calcEigenValsVecs()函数

static void calcEigenValsVecs( const Mat& _cov, Mat& _dst )
{
    Size size = _cov.size();
    if( _cov.isContinuous() && _dst.isContinuous() )
    {
        size.width *= size.height;
        size.height = 1;
    }

    for( int i = 0; i < size.height; i++ )
    {
        const float* cov = _cov.ptr<float>(i);
        float* dst = _dst.ptr<float>(i);

         //调用该函数计算2x2协方差矩阵的特征值和特征向量
        eigen2x2(cov, dst, size.width);
    }
}

该函数中调用eigen2x2()函数计算每个像素点处协方差矩阵的2个特征值和2个特征向量，协方差矩阵为如下形式，数据都保存在cov的三个通道中：

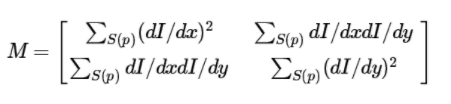
static void eigen2x2( const float* cov, float* dst, int n )
{
    for( int j = 0; j < n; j++ )
    {
        double a = cov[j*3];
        double b = cov[j*3+1];
        double c = cov[j*3+2];

        double u = (a + c)*0.5;
        double v = std::sqrt((a - c)*(a - c)*0.25 + b*b);
　　　　　
　　　　　//计算两个特征值l1,l2
        double l1 = u + v;
        double l2 = u - v;

　　　　　//计算特征值l1对应的特征向量
        double x = b;
        double y = l1 - a;
        double e = fabs(x);

        if( e + fabs(y) < 1e-4 )
        {
            y = b;
            x = l1 - c;
            e = fabs(x);
            if( e + fabs(y) < 1e-4 )
            {
                e = 1./(e + fabs(y) + FLT_EPSILON);
                x *= e, y *= e;
            }
        }

        double d = 1./std::sqrt(x*x + y*y + DBL_EPSILON);
         //保存特征值l1及其对应的特征向量
        dst[6*j] = (float)l1;
        dst[6*j + 2] = (float)(x*d);
        dst[6*j + 3] = (float)(y*d);

        //计算特征值l2对应的特征向量
        x = b;
        y = l2 - a;
        e = fabs(x);

        if( e + fabs(y) < 1e-4 )
        {
            y = b;
            x = l2 - c;
            e = fabs(x);
            if( e + fabs(y) < 1e-4 )
            {
                e = 1./(e + fabs(y) + FLT_EPSILON);
                x *= e, y *= e;
            }
        }

        d = 1./std::sqrt(x*x + y*y + DBL_EPSILON);
        //保存特征值l2及其对应的特征向量
        dst[6*j + 1] = (float)l2;
        dst[6*j + 4] = (float)(x*d);
        dst[6*j + 5] = (float)(y*d);
    }
}

求得2个特征值α、β和2个特征向量之后，就是要利用特征值构建特征表达式，通过表达式的值（ (αβ) - k(α+β)^2 ）来区分角点，k的值通常设置为0.04：

for( int j = 0; j < src_gray.rows; j++ )
   { for( int i = 0; i < src_gray.cols; i++ )
        {
          float lambda_1 = myHarris_dst.at<Vec6f>(j, i)[0];
          float lambda_2 = myHarris_dst.at<Vec6f>(j, i)[1];
          Mc.at<float>(j,i) = lambda_1*lambda_2 - 0.04f*pow( ( lambda_1 + lambda_2 ), 2 );
        }
   }

代码中利用 minMaxLoc( Mc, &myHarris_minVal, &myHarris_maxVal, 0, 0, Mat() ); 函数获取特征表达式的最大值min和最小值max，通过选取不同的阈值min<=thresh<=max，来指定大于阈值thresh的表达式值对应的点为检测出的角点。

posted @ 2020-09-10 20:33 码我疯狂的码阅读(260) 评论(0) 编辑收藏举报

刷新页面返回顶部

码我疯狂的码

Harris角点

Harris角点

公告