光度立体

参考自：https://zhuanlan.zhihu.com/p/205778332
http://pages.cs.wisc.edu/~csverma/CS766_09/Stereo/stereo.html

光度立体

光度立体法，即Photometric Stereo, 最早是由当时在MIT的人工智能实验室的Robert J. Woodham教授在1978年左右提出。

什么是光度立体

光度立体是一种使用多个光源方向估计表面几何形状的方法

这种方法的用途是可以重建出物体表面的法向量，以及物体不同表面点的反射率，最关键的是它不像传统的几何重建（例如立体匹配）方法那样需要去考虑图像的匹配问题，因为所需要做的只是采集三张以上，由不同方向的光照射物体的图像。这个过程中，物体和相机都不动，因此图像天然就是对齐的，这使得整个过程非常的简洁。

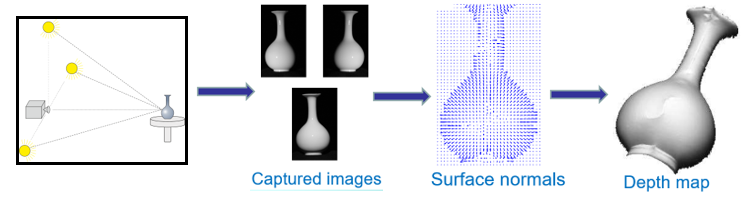
为什么使用光度立体

光度立体捕获反射率数据以进行2D匹配

与其他方法的比较：

光度立体法和传统几何重建法的比较：

传统几何重建法	光度立体法
准确获取深度	获取表面梯度
粗糙表面，梯度方向不同时效果好	连续、光滑的表面效果最好
带有纹理的表面，具有不同反射的表面效果较好	均匀一致的表面效果最好
需要图像对齐、困难	不需要图像对齐
不能获取表面反射比例	可以获取表面反射比例
	许多情况下，根据表面方向描述对象行形状比根据参考屏幕上方的范围或高度描述更可取

基础方法

假设：

没有投影/自阴影或高光
灰度/线性成像
入射光由远处的单一点光源发出，这样照射到物体表面每一点的光的方向一致，强度一致
相机的投影是正交投影，图像上的点的坐标可以直接反映三维物体的表面坐标
表面静止不动
物体表面具有lambertian反射特性，即它对入射光产生漫反射，在每个方向上反射的光强都是一致的

$$ I\propto cos\theta = N · L $$ 其中：

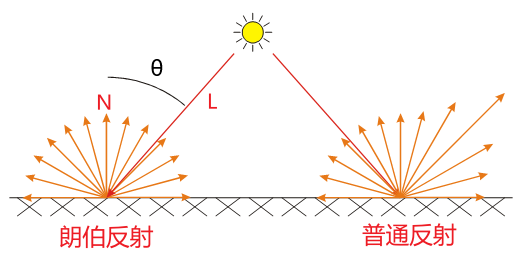
$I ：$辐射强度
$N:$单位法向量
$L:$ 单位光源向量
$\theta$：$N$和$L$之间的夹角

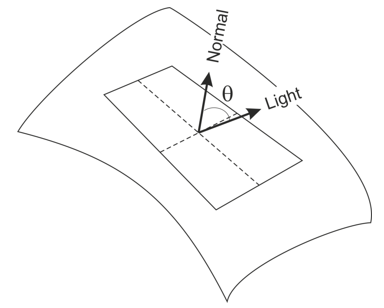
平面方程：

\[Ax+By+Cz+D = 0 \]

平面法线向量：

\[N = [A,B,C]^T \]

由于$z = -\frac{A}{C}x - \frac{B}{C}y - \frac{D}{C}$，所以梯度为：

\[\frac{\partial z}{\partial x} = -\frac{A}{C}\qquad\qquad \frac{\partial z}{\partial y} = - \frac{B}{C} \]

重新缩放表面法线

\[n = [\frac{A}{C},\frac{B}{C},1]^T = [-\frac{\partial z}{\partial x},-\frac{\partial z}{\partial y}, 1]^T \]

上式揭示了法向量与梯度之间的关系

考虑使用一个光源对物体进行成像

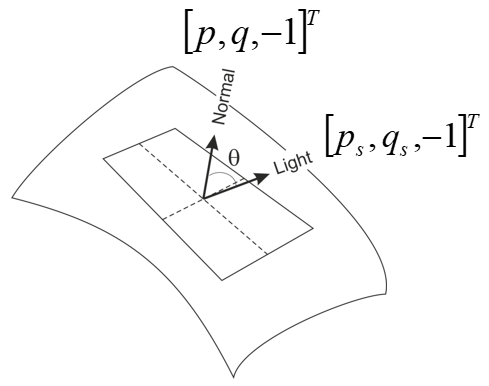
朗伯仿射模型：

\[E = \rho L cos\theta \]

其中：

$E:$散射
$\rho:$反射率
$L:$光照强度（可忽略）（注意区分这里的L与上面表示光源向量的L表示的不同含义）

取法向量和光源向量的向量积得到$cos\theta$

\[pp_s + qq_s + 1 = \sqrt{p^2+q^2+1}\sqrt{p_s^2+q_s^2+1}cos\theta \]

把上式的$cos\theta$代入到朗伯定律

\[E = \rho L \frac{pp_s+qq_s+1}{\sqrt{p^2+q^2+1}\sqrt{p_s^2+q_s^2+1}} \]

如果反射率被重新定义且相机响应是线性的，则

\[I' = \rho'\frac{pp_s+qq_s+1}{\sqrt{p^2+q^2+1}\sqrt{p_s^2+q_s^2+1}} \]

已知量：$p_s,q_s,I$

未知量：$p,q,\rho$

一个方程求三个未知数，是无法求解的，因此至少需要三个方程，即三个光源去照射物体才可以进行求解。

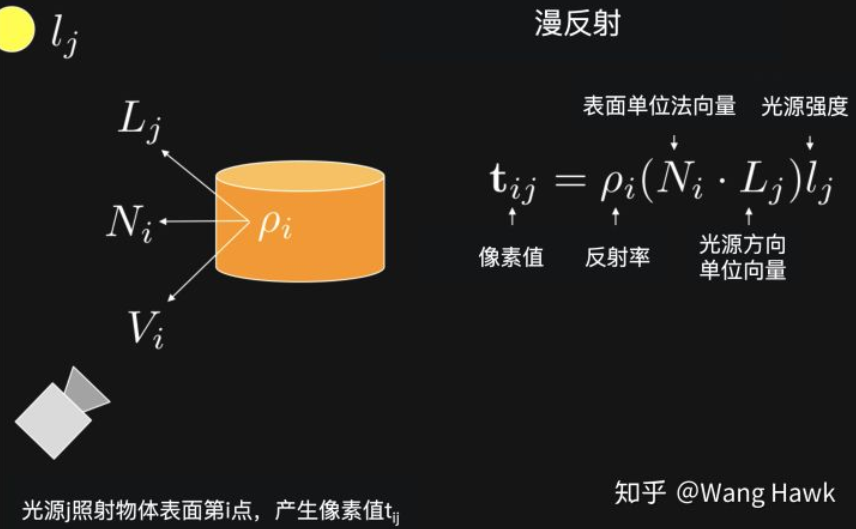
这里面，$\rho$和$N$代表了物体表面的特性，而L和l则代表了光源的方向和强度，于是可以分别合并表示如下。

$N$和$L$都是三维空间中的$3\times 1$的单位向量，光源的强度可以用常量1表示。像素值$t$可以直接通过图像获得，右边的光源方向可以提前标定求得。那么，就可以在物体和相机都不动的情况下，用至少三个不共面的光线照射物体表面第$i$点，从而将$N$和 $\rho$求解出来：

设三个光源方向向量构成矩阵$L = [L_1,L_2,L_3]^T$，对应的三个像素值构成向量$t_i$，那么有

\[\rho_i = |L^{-1}t_i|\\ N_i = \frac{1}{\rho_i}L^{-1}t_i \]

由于光源照射物体表面时，有可能会产生阴影，这样三个光源无法同时照亮的区域就会无法求解出结果。所以通常可以采用更多的光源从不同方向分别照亮物体并成像来解决这个问题。

假设有$n>=3$个光源，那么则有：

\[L = [L_1,L_2,L_3,...,L_n]^T\\ t_i = [t_{i1},t_{i2},t_{i3},...,t_{in}]^T = \rho_iLN_i \]

那么

\[\rho_i = |(L^TL)^{-1}L^Tt_i|\\ N_i = \frac{1}{\rho}(L^TL)^{-1}Lt_i \]

几种不同的情况：

$p_s=q_s=0 $相当于光线垂直照射

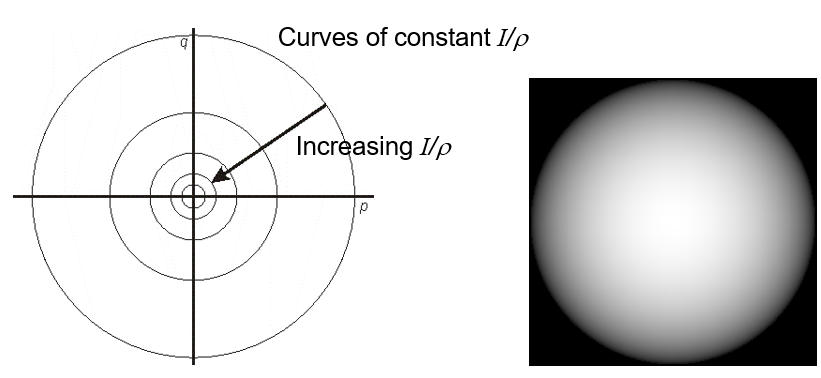
$p_s=q_s=0.5$ 相当于斜着照射

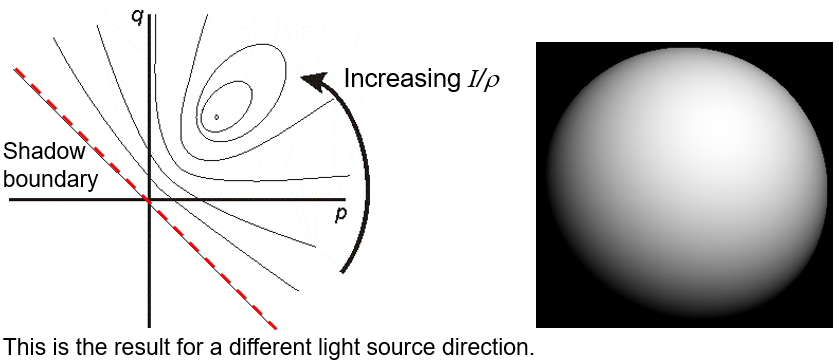
使用圆锥曲线表示：

使用单位圆表示：

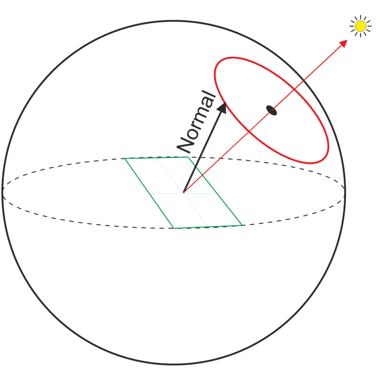
因此，光度立体实际上是使用多个光源方向对物体进行照射。

基本过程

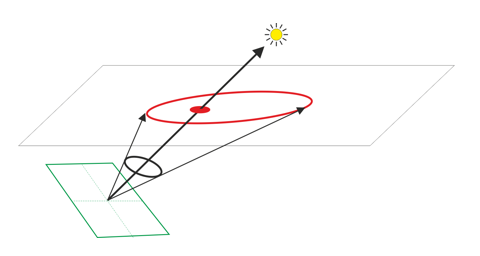
光源方向的标定

先第一步，是进行光源方向的标定，一种可行的方法是在场景中放入一个光滑的球并在不同光源下成像，这样球的表面高亮处就会反映光源的方向

光源方向$L$，球表面法向量$N$以及反射方向$R$之间的关系如下

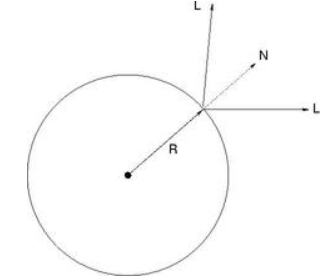
有

\[L = 2(N·R)·N - R \]

其中$R$是反射方向，取为$(0,0,1)$，是观察者到物体的向量。$(P_x,P_y)$是图像上最亮点的坐标，$(C_x,C_y)$是图像上球心的坐标

那么$N$的表达式为：

\[N_x = P_x - C_x\\ N_y = P_y - C_y\\ N_z = \sqrt{R^2 - N^2_x - N^2_y} \]

利用$N$和$R$，就可以求得光源方向$L$

计算法向量图和深度图

利用上面讲过的原理和公式，可以很容易求得物体表面上每一个被足够多的光源照亮的点的法向量。接下来的关键则是利用法向量图，获取深度图。

投影关系如下图所示：

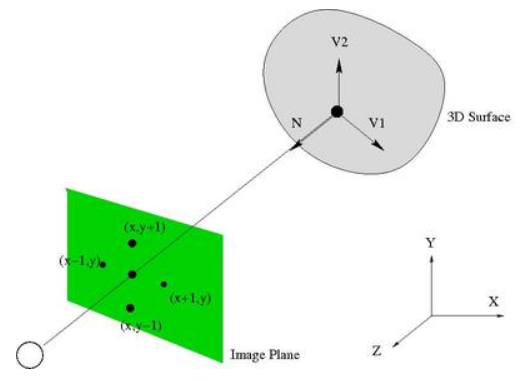
物体表面法向量$N$与物体表面上的向量$V_1$及$V_2$垂直，那么有：

\[\begin{eqnarray} V_1 &=& (x+1,y,z_{x+1,y})-(x,y,z_{x,y}) \\&=& (1, 0, z_{x+1,y} - z_{x,y})\\ NV_1 &=& 0\\ (n_x,n_y,n_z) · (1, 0, z_{x+1,y} - z_{x,y}) &=& 0\\ n_x + n_z(z_{x+1,y} - z_{x,y}) &=& 0 \end{eqnarray} \]

以及

\[\begin{eqnarray} V_2 &=& (x,y+1,z_{x,y+1})-(x,y,z_{x,y}) \\&=& (0, 1, z_{x,y+1} - z_{x,y})\\ NV_2 &=& 0\\ (n_x,n_y,n_z) · (0, 1, z_{x,y+1} - z_{x,y}) &=& 0\\ n_y + n_z(z_{x,y+1} - z_{x,y}) &=& 0 \end{eqnarray} \]

上面两个式子，会构成一个线性表达式：

\[Mz = v \]

其中$v$由各个像素点的法向量技术而得，$M$则是一个尺寸为$(2\times m, m)$的稀疏矩阵，其中$m$为像素个数，$z$则是各个像素点的深度坐标构成

通过使方程对称且为正定，通过共轭梯度法的最小二乘法来求解这种超定线性方程组，最终得到深度图