对极几何

参考自：视觉SLAM14讲、鲁鹏《计算机视觉》

对极几何

对极几何是两幅视图之间内在的射影几何，它独立于景物结构，只依赖于摄像机的内参数和相对姿态。

极几何

极几何描述了同一场景或者物体的两个视点图像间的几何关系

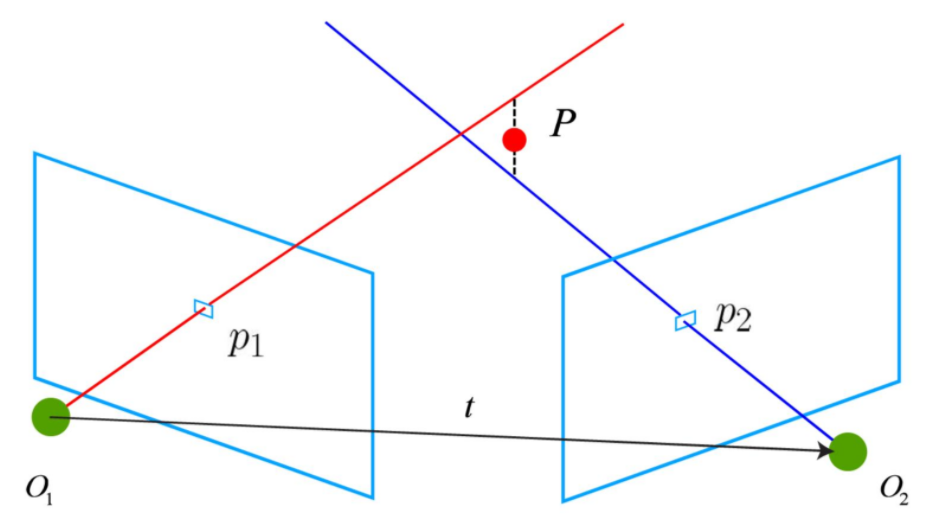
假设已经从两张图像中得到了一对配对好的特征点，希望求取两帧图像\(I_1,I_2\)之间的运动，假设第一帧到第二帧的运动为\(R,t\)，\(O_1,O_2\)是两个摄像机中心，\(I_1\)中有一个特征点\(p_1\)，在\(I_2\)中对应特征点\(p_2\)，两者是通过特征匹配得到的。如果匹配正确，说明它们是同一个空间点在两个成像平面上的投影

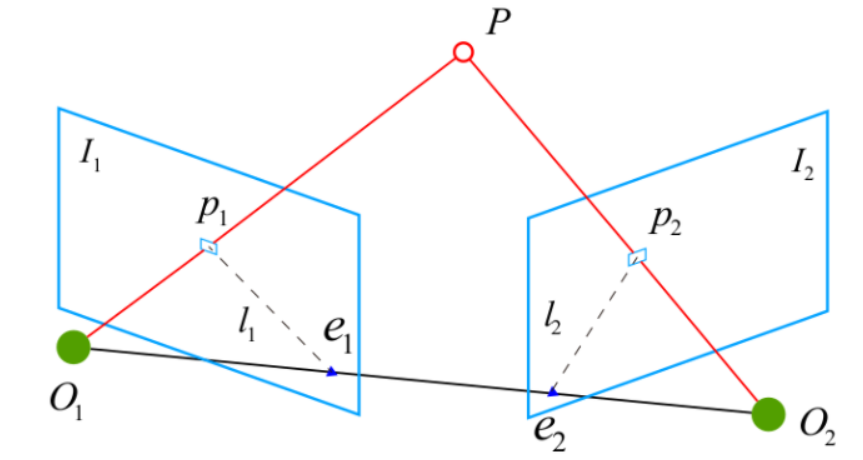
• 极平面：过点\(P\)，\(O_1\)与\(O_2\)的平面
• 基线：\(O_1\)与\(O_2\)的连线
• 极线：极平面与成像平面的交线\(l_1,l_2\)
• 极点：基线与成像平面的交点\(e_1,e_2\)

性质：

• 极平面相交于基线
• 极线相交于极点
• \(p\)的对应点在极线\(l'\)上
• \(p'\)的对应点在极线\(l\)上

特例：平行视图

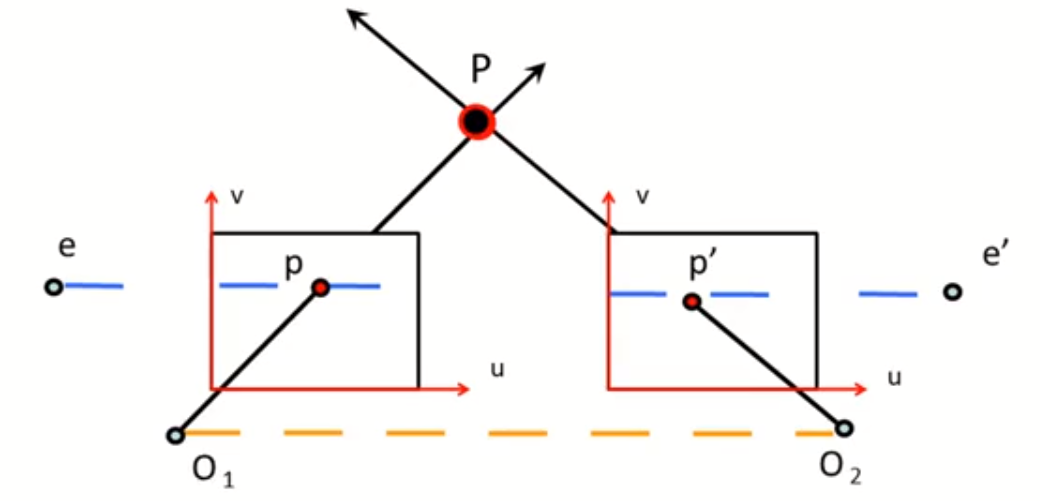
• 两个图像平面平行
• 基线平行于图像平面，极点\(e\)和\(e'\)位于无穷远处
• 极线平行于图像坐标系的\(u\)轴

特例2：前向平移（无旋转）

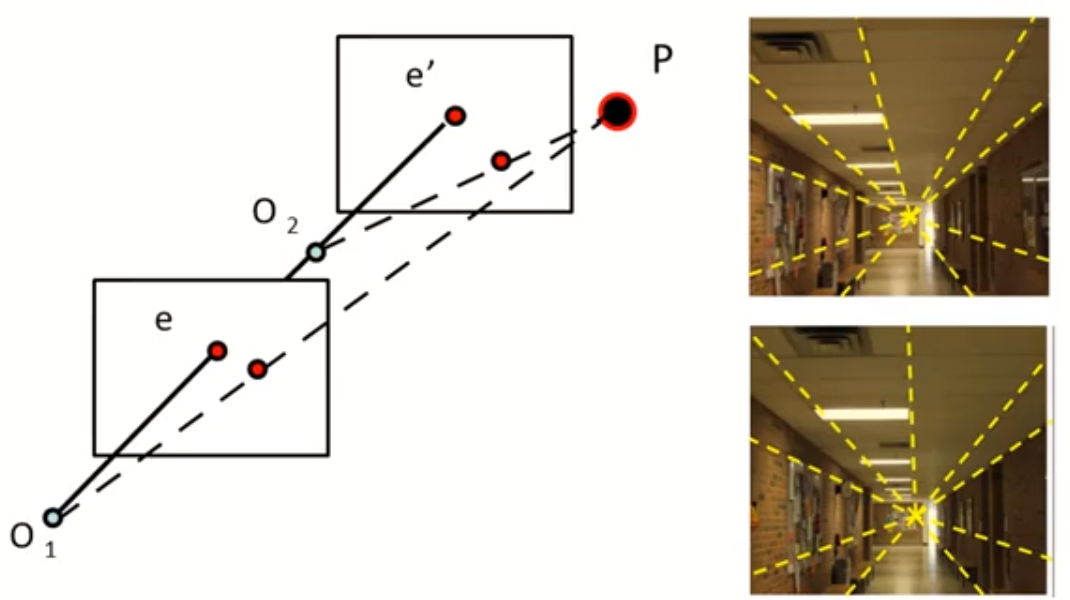
两幅图上极点位置相同，极点称作展开焦点

对应关系：已知一个图像中的\(p\)点，如何在另外一个图像中找到\(p'\)点？

通过极几何约束，将搜索范围缩小到对应的极线上

从第一帧角度看，射线\(\vec{O_1p_1}\)是某个像素可能出现的空间位置——因为该射线上所有点都会投影到同一个像素点。同时，如果不知道P的位置，那么在第二幅图上看时，连线\(\vec{e_2p_2}\)（第二幅图中的极线）就是P可能出现的投影位置，也就是射线\(\vec{O_1p_1}\)在第二个相机中的投影。

由于通过特征点匹配确定了\(p_2\)的像素位置，所有能够推断\(P\)的空间位置以及相机运动。

基础矩阵和本质矩阵

在第一帧的坐标系下，设P在相机坐标系下，坐标为\(P=[X,Y,Z]^T\)

\(p_1,p_2\)的像素坐标（单位像素）：\(s_1p_1=KP,s_2p_2=K(RP+t)\)

有时使用齐次坐标表示像素点。在使用齐次坐标时，一个向量将等于它自身乘任意非零常数。这通常用于表达一个投影关系。例如，\(s_1p_1\)和\(p_1\)成投影关系，他们在齐次坐标系下的意义是相等的。称这种相等关系为尺度意义下的相等。

\[sp\simeq p \]

那么上述两个投影关系可写为\(p_1\simeq KP, p_2\simeq K(RP+T)\)

其归一化平面坐标：\(x_1=K^{-1}p_1,x_2=K^{-1}p_2\)

得到：\(x_2\simeq Rx_1+T\) 这里的x是齐次坐标，等式表达了一个齐次关系

两边同乘\(T^\prime\)，相当于与它做外积，得到的结果和它、\(x_2\)都垂直。因此再左乘\(x_2^T\)，就得到了0

最终得到\(x_2^TT^\prime Rx_1 = 0\)

中间部分写作E矩阵，称为本质矩阵：

\[x_2^TEx_1=0\\ E=T^\prime R \]

带入\(p_1,p_2\)：

\[p_2K^{-T}T^\prime RK^{-1}p_1=0\\ E=T'R \]

中间部分写作F矩阵，称为基础矩阵：

\[p_2Fp_1=0\\ F=K^{-T}T'RK^{-1} \]

\(T^\prime\)是\(T\)的反对称矩阵。

这两个式子称为对极约束。根据对极约束，估计R，t的方法为：

1. 根据匹配点的位置，求出E或者F
2. 根据E或者F，求出R，T

性质：

本质矩阵：

• \(p_1\)对应的极线是\(l_2\)\((l_2 = Ep_1)\)
• \(p_2\)对应的极线是\(l_1(l_1=E^Tp_2)\)
• \(Ee_1=0\)与\(E^Te_2=0\)
• \(E\)是奇异的（秩为2），奇异值必定是\([\sigma,\sigma,0]^T\)的形式
• \(E\)有5个自由度（3旋转+3平移，\(det(E) = 0\)去掉一个自由度）

本质矩阵是两个标准相机相对关系的内参，换言之，给定两个已标定相机的相对位置关系，本质矩阵即被确定。

基础矩阵

• \(p_1\)对应的极线是\(l_2\)\((l_2 = Fp_1)\)
• \(p_2\)对应的极线是\(l_1(l_1=F^Tp_2)\)
• \(Fe_1=0\)与\(F^Te_2=0\)
• \(F\)是奇异的（秩为2）
• $F $有7个自由度（9 - 尺度无法确定 - \(det(F) = 0\)）

基础矩阵是任意两个相机相对关系的内参，换言之，给定了两个相机的相对位置关系和相机内参，基础矩阵即被确定。

基础矩阵的作用：已知\(F\)，无需场景信息以及摄像机内、外参数，即可建立左右图像对应关系。

估计基础矩阵

F矩阵有7个自由度，理论上7个点即可求解F，但计算方法比较复杂

\[p'^TFp=0\qquad p = \left[ \begin{matrix} u\\v\\1 \end{matrix} \right]\qquad p' = \left[ \begin{matrix} u'\\v'\\1 \end{matrix} \right]\\ \Downarrow\\ (u',v',1)\left( \begin{matrix} F_{11} & F_{12} & F_{13}\\ F_{21} & F_{22} & F_{23}\\ F_{31} & F_{32} & F_{33}\\ \end{matrix} \right)\left( \begin{matrix} u\\v\\1 \end{matrix} \right)=0 \\\Downarrow\\ (uu',vu',u',uv',vv',v',u,v,1)\left( \begin{matrix} F_{11}\\F_{12}\\F_{13}\\F_{21}\\F_{22}\\F_{23}\\F_{31}\\F_{32}\\F_{33} \end{matrix} \right)=0 \]

选取8组对应点

• 齐次系统\(Wf = 0\)

• 秩 = 8 \(\longrightarrow\) 存在唯一非零解

• 秩 > 8 \(\overset{最小二乘解}{\longrightarrow}\) \(\mathop {min}\limits_{f}||Wf|| \qquad s.t.||f||=1\) \(\overset{SVD}{\longrightarrow}\hat{F}\) f为W矩阵最小奇异值的右奇异向量，且\(||f||=1\)

但\(\hat{F}\)不是我们要求的基础矩阵，基础矩阵的秩为2，但\(\hat{F}\)通常秩为3，即\(\hat{F}\)满秩

寻找F最小化 \(||F-\hat{F}||_F\qquad\qquad s.t. det(F)=0\)

\[SVD(\hat{F}) = U \left[ \begin{matrix} s_1 & 0 & 0\\0 & s_2 & 0\\0 & 0 & s_3 \end{matrix} \right]V^T \longrightarrow F = U \left[ \begin{matrix} s_1 & 0 & 0\\0 & s_2 & 0\\0 & 0 & 0 \end{matrix} \right]V^T \]

八点算法

1. 构建W矩阵

2. 对W矩阵进行奇异值分解求\(\hat{F}\)， f为W矩阵最小奇异值的右奇异向量，且\(||f|| = 1\)

3. 执行秩为2的约束\(\longrightarrow\)F

   \(SVD(\hat{F}) = U\left[\begin{matrix} s_1 & 0 & 0\\0 & s_2 & 0\\0 & 0 & s_3 \end{matrix} \right]V^T \longrightarrow F = U \left[ \begin{matrix} s_1 & 0 & 0\\0 & s_2 & 0\\0 & 0 & 0 \end{matrix} \right]V^T\)

存在的问题

由于W中各个元素的数值差异过大，且SVD分解有数值计算问题，所以八点法精度较低

改进： 归一化八点法（精度高）

对每幅图像施加变换T（平移和缩放），让其满足如下条件：

• 原点 = 图像上点的重心
• 各个像点到坐标原点的均方根距离等于\(\sqrt{2}\)（或者均方距离等于2）

步骤：

1. 分别计算左图和右图的T和T’
2. 坐标归一化：\(q_i = Tp_i \qquad q_i' = T'p_i'\)
3. 通过八点法计算矩阵\(F_q\)
4. 逆归一化 \(F = T'^TF_qT\)

单应性矩阵

单应(Homography)是射影几何中的概念，又称为射影变换。它把一个射影平面上的点(三维齐次矢量)映射到另一个射影平面上，并且把直线映射为直线，具有保线性质。

总的来说，单应是关于三维齐次矢量的一种线性变换，可以用一个\(3×3\)的非奇异矩阵\(H\)表示

\[x_1 = Hx_2 \]

这是一个齐次坐标的等式，\(H\)乘以一个非零的比例因子上述等式仍然成立，即\(H\)是一个\(3×3\)齐次矩阵，具有8个未知量。

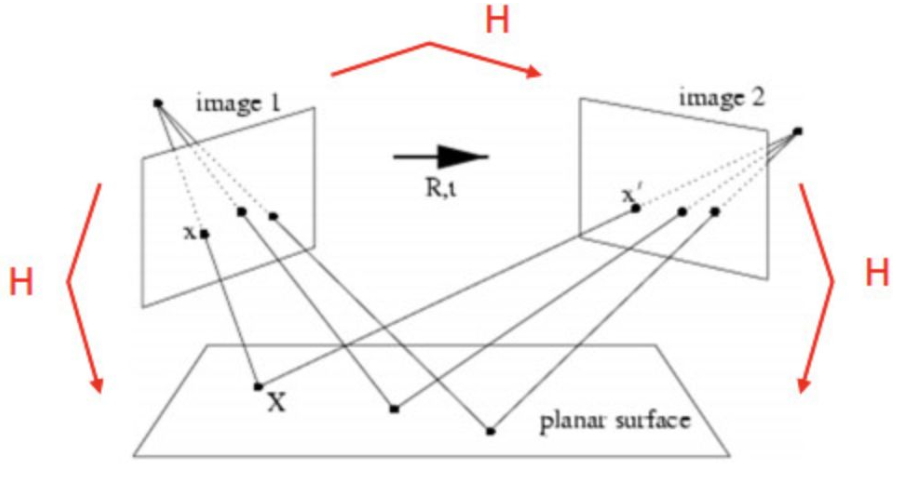
假设已经取得了两图像之间的单应，则可单应矩阵\(H\)可以将两幅图像关联起来

\[\left( \begin{matrix} u_1\\v_1\\1 \end{matrix} \right)=H \left( \begin{matrix} u_2\\v_2\\1 \end{matrix} \right) \]

其中\((u_1,v_1,1)^T\)表示图像1中的点，\((u_2,v_2,1)^T\)表示图像2中的点，也就是可以通过单应性矩阵\(H\)将图像2变换到图像1，因此也很多实际应用，例如：图像的校正、对齐以及在SLAM中估计两个相机间的运动。

设图像\(I_1\)和\(I_2\)有一对已经匹配好的特征点\(p_1\)和\(p_2\)，这个特征点落在平面\(P\)上，平面在第一个相机坐标系下的单位法向量为n，距离第一个相机中心（坐标原点）为d，设这个平面满足方程：

\[n^TP+d = 0 \]

整理得：

\[-\frac{n^TP}{d} = 1 \]

又因为像素点\(p_2\)的位置为：\(p_2\simeq K(RP+t)\)

得：

\[\begin{eqnarray} p_2&\simeq& K(RP+t)\\ &\simeq&K(RP+t·(-\frac{n^TP}{d}))\\ &\simeq&K(R-\frac{tn^T}{d})P\\ &\simeq&K(R-\frac{tn^T}{d})K^{-1}p_1 \end{eqnarray} \]

于是得到了一个直接描述图像坐标\(p_1\)和\(p_2\)之间的变换，中间部分记作\(H\)，于是

\[H = K(R-\frac{tn^T}{d})K^{-1}\\ p_2 \simeq Hp_1 \]

它的定义与旋转，平移及平面的参数有关。与基础矩阵F类似，单应矩阵H也是一个\(3\times 3\)的矩阵，求解思路与F类似，同样可以根据匹配点计算H，然后分解以计算旋转和平移。把上式展开得：

\[\left( \begin{matrix} u_2\\v_2\\1 \end{matrix} \right) \simeq \left( \begin{matrix} h_1 & h_2 & h_3\\ h_4 & h_5 & h_6\\ h_7 & h_8 & h_9 \end{matrix} \right) \left( \begin{matrix} u_1\\v_1\\1 \end{matrix} \right) \]

注意，这里依然不是等号，所以H矩阵也可以乘任意非零常数。

在实际处理中可以令\(h_9 = 1\)。根据第3行去掉这个非零因子，有

\[u_2 = \frac{h_1u_1 + h_2v_1+h_3}{h_7u_1+h_8v_1+h_9}\\ v_2 = \frac{h_4u_1 + h_5v_1+h_6}{h_7u_1+h_8v_1+h_9} \]

整理得：

\[h_1u_1+h_2v_1+h_3-h_7u_1u_2-h_8v_1u_2 = u_2\\ h_4u_1+h_5v_1+h_6-h_7u_1v_2-h_8v_1v_2=v_2 \]

这样一组匹配点对就可以构造出两项约束（事实上有三项约束，但是因为线性相关，只取前两个），于是自由度为8的单应矩阵可以通过4对匹配特征点算出。

这种做法把\(H\)看作向量，通过解该向量的线性方程来恢复\(H\)，又称直接线性变换法。与本质矩阵相似，求出单应矩阵以后需要对其进行分解，才可以得到相应的旋转矩阵R和平移向量t。

单应性在SLAM中具有重要意义，当特征点共面或者相机发生纯旋转时，基础矩阵的自由度下降，这就出现了所谓的退化（degenerate）。现实中的数据包含一些噪声，这是如果继续使用八点法求解基础矩阵，基础矩阵多出来的自由度将会主要由噪声决定。为了能够避免退化现象造成的影响，通常我们同时估计基础矩阵F和单应矩阵H，选择重投影误差比较小的那个作为最终的运动估计矩阵。

存在的问题

尺度不确定性：

对t长度的归一化，直接导致了单目视觉尺度的不确定性。例如，程序中输出的t第一维为0.82，但究竟是米还是厘米是无法确定的。因为对t乘以任意比例常数后，对极约束依然成立。

在单目视觉中，我们对两张图像的t归一化相当于固定了尺度，以这时的t为单位1，计算相机运动和特征点的3D位置。这称为单目SLAM的初始化。在初始化后就可以用3D-2D计算相机运动了。初始化之后的轨迹和地图的单位就是初始化时固定的尺度。

因此，单目SLAM有一步不可避免的初始化。初始化的两张图像必须有一定程度的平移，而后的轨迹和地图都将以此步的平移为单位。

除了对t进行归一化，还可以令初始化时所有的特征点平均深度为1，也可以固定一个尺度。相比于令t长度为1的做法，把特征点深度归一化可以控制场均的规模大小，让数值更稳定。

初始化纯旋转问题：

从F分解到R,t的过程中，如果相机发生的是纯旋转，导致t为0，那么得到的F也将为0，导致无从求解R。不过此时可以依靠H求取旋转，但仅有旋转时，我们无法用三角测量估计特征点的空间位置。所以，单目初始化不能只有纯旋转，必须要有一定程度的平移。

多于8对点的情况：

计算最小二乘解，存在误匹配时使用RANSAC来求。

三角测量

在得到运动之后，下一步需要用相机的运动估计特征点的空间位置。单目SLAM中，仅通过但张图像无法获得像素的深度信息，需要通过三角测量的方法估计图点的深度。

三角测量是指，通过不同的位置对同一个路标点进行观察，从观察到的位置推断路标点的距离。

考虑图像\(I_1,I_2\)，以左图为参考，右图的变换矩阵为T。相机光心为\(O_1\)和\(O_2\)，在\(I_1\)中有特征点\(p_1\)，在\(I_2\)中有特征点\(p_2\)。理论上直线\(O_1p_1\)和\(O_2p_2\)在场景中会相交于一点P，该点即两个特征点所对应的地图点在三维场景中的位置。然而由于噪声的影响，这两个点往往无法相交，因此可以通过最小二乘法求解。

设\(x_1,x_2\)为两个特征点的归一化坐标，那么它们满足：

\[s_2x_2 = s_1Rx_1 + t \]

已知\(R,t\)，想求解两个特征点的深度\(s_1,s_2\)。先对上式左乘一个\(x_2^\wedge\)，得到

\[s_2x_2^\wedge x_2 = 0 = s_1x_2^\wedge Rx_1 + x_2^\wedge t \]

该式左侧为0，右侧可以看成是一个\(s_2\)的方程，可以根据它直接求得\(s_2\)，进而求得\(s_1\)，于是就得到了两帧下的深度，确定了它们的空间坐标。由于噪声的存在，R,t不一定准确使得上式为0，更常见的做法是求最小二乘解。