图像处理坐标系转换参考表
图像处理坐标系转换
图像处理涉及以下四个坐标系：
\(O_w-X_wY_wZ_w\)：世界坐标系，描述相机位置，单位mm
\(O_c-X_cY_cZ_c\)：相机坐标系，光心为原点，单位mm
\(O-xy\)：图像坐标系，光心为图像中点，单位mm
\(uv\)：像素坐标系，原点为图像左上角，单位pixel
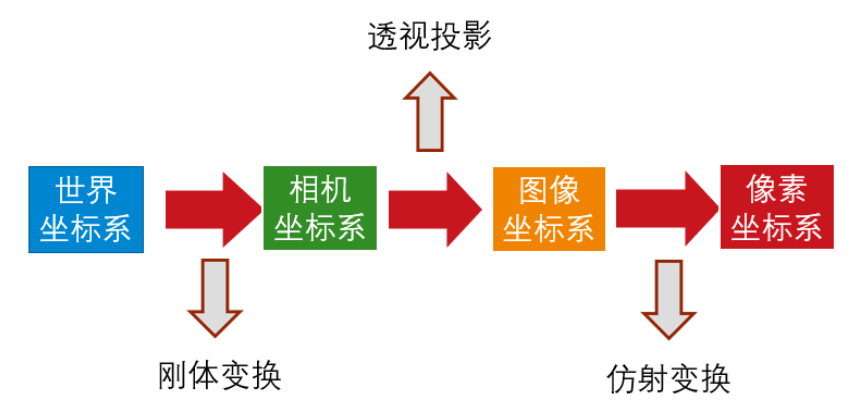
世界坐标系\(\longrightarrow\)摄像机坐标系
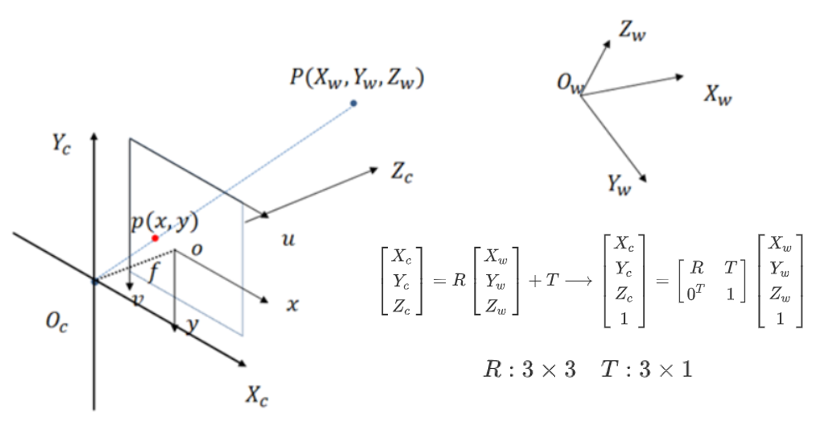
相机坐标系\(\longrightarrow\)图像坐标系
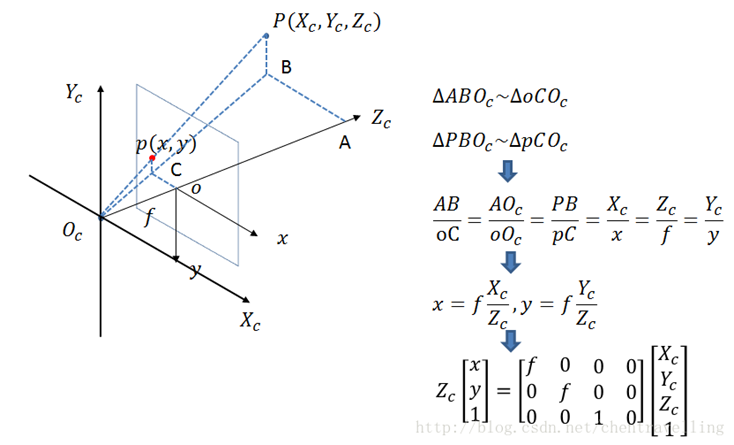
图像坐标系\(\longrightarrow\)像素坐标系
整体坐标系转换：
\[z_c \left[
\begin{matrix}
u\\v\\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
\frac{1}{dx} & 0 & u_0\\
0 & \frac{1}{dy} & v_0\\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
f & 0 & 0 & 0\\
0 & f & 0 & 0\\
0 & 0 & 1 & 0
\end{matrix}
\right]
\left[
\begin{matrix}
R & t \\
0^T & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x_w\\y_w\\z_w\\1
\end{matrix}
\right]
\]
由于制造工艺的精度问题，会有一定误差，同样的，感光阵列的法向和相机光轴也不是完全重合，即可以看作成像平面与光轴不垂直。
所以
\[u = u_0 + \frac{x_d}{dx} - \frac{y_dcot\theta}{dx}\\
v = v_0 + \frac{y_d}{dysin\theta}
\]
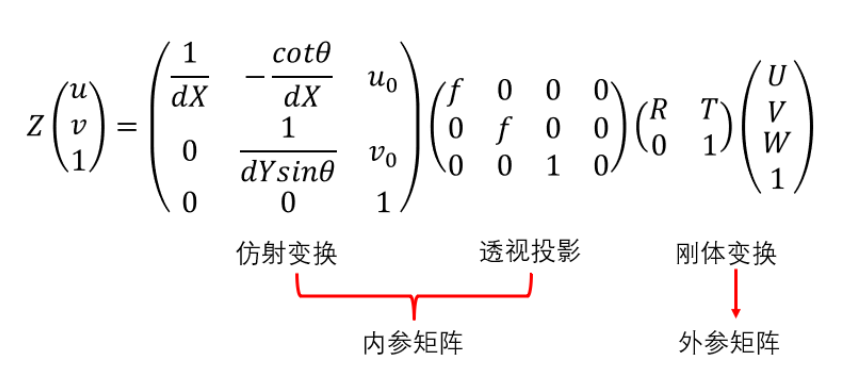
则整体坐标系转换进一步可以写为：
\[z_c \left[
\begin{matrix}
u\\v\\1
\end{matrix}
\right]
=
\left[
\begin{matrix}
\frac{1}{dx} & -\frac{cot\theta}{dx} & u_0\\
0 & \frac{1}{dysin\theta} & v_0\\
0 & 0 & 1
\end{matrix}
\right]
\left[
\begin{matrix}
f & 0 & 0 & 0\\
0 & f & 0 & 0\\
0 & 0 & 1 & 0
\end{matrix}
\right]
\left[
\begin{matrix}
R & t \\
0^T & 1
\end{matrix}
\right]
\left[
\begin{matrix}
x_w\\y_w\\z_w\\1
\end{matrix}
\right]
\]
