Refractive laser triangulation and photometric stereo in underwater environment学习笔记

前半部分推导了水下虚拟成像和现实坐标之间的关系，后面没看懂，等以后补上。

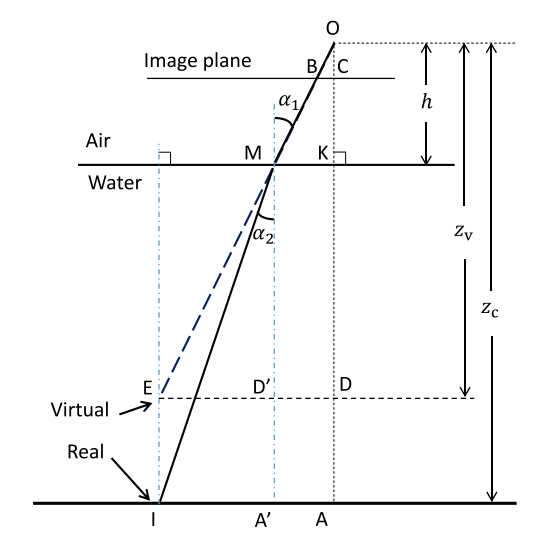
相机处于防水外壳中。 相机的光轴垂直于外壳接口。 根据透视投影，可以将虚拟点设置为沿OM的延长线的任何位置。 为了简化计算，我们假设虚拟点在真实点的正上方，并且两个点的连接线垂直于外壳接口。

该模型的特征在于以下参数：

\(h\)：透视中心\(O\)与外壳接口之间的距离；

\(α_1\)：入射角；\(α_2\)：在水中的折射角；

\(I\)：真实物体点\(（x_c，y_c，z_c）\)（在相机坐标系中）；

\(E\)：与点\(I\)相关的虚拟对象点\(（x_v，y_v，z_v）\)。

在此模型中，显然存在以下关系：\(x_c = x_v，y_c = y_v\)。

假设光轴，入射光线和折射光线都在同一平面上。 根据斯涅耳的折射定律，折射率n可以写成：

\[n = \frac{sin \alpha_1}{sin \alpha_2} \]

根据几何关系：

\[sin\alpha_1 = \frac{ED'}{ME}\\ sin\alpha_2 = \frac{IA'}{MI} \]

在图中存在如下的几何关系：

\(ED = IA,ED' = IA',MD'=KD,MA'=KA, AA'=DD'=MK\)

因此折射率\(n\)可以写为

\[n = \frac{ED' \times MI}{IA' \times ME} = \frac{MI}{ME} \]

因为\(z_v = OD,z_c = OA\)，则可以由\(OA\)和\(OD\)的几何关系来估计“虚拟现实”关系，

他们有一个共同的因素\(\longrightarrow OK\)

\[OA = OK + KA\\ OD = OK + KD \]

其中\(OK\)表示镜头玻璃距离\(h\)，下面找到\(KA\)和\(KD\)的几何关系

\[\begin{eqnarray} KA &=& \sqrt{MI^2- IA'^2} \\ &=& \sqrt{n^2 \times ME^2 - IA'^2}\\ &=& \sqrt{n^2 \times (MD'^2 + ED'^2) - IA'^2}\\ &=& \sqrt{n^2 \times (KD^2 + IA'^2) - IA'^2}\\ &=& \sqrt{n^2 \times KD^2 + (n^2-1) \times IA'^2} \end{eqnarray} \]

又因为\(KD = OD - OK， IA' = IA - AA' = IA - MK\)，因此\(KA\)可以被表示为

\[KA = \sqrt{n^2 \times (OD - OK)^2 + (n^2 - 1) \times (IA - MK) ^ 2} \]

因此\(OA\)可以表示为

\[OA = OK + \sqrt{n^2 \times (OD - OK)^2 + (n^2 - 1) \times (IA - MK) ^ 2} \]

所以，\(z_v\)和\(z_c\)的关系可以表示为

\[z_c = h +\sqrt{n^2 \times (z_v - h)^2 + (n^2 - 1) \times (IA - MK) ^ 2} \]

基于透视相机模型，点\(I\)和\(E\)都与点\(B(x_u,x_v)\)有关（在归一化坐标系中）。它们之间的关系可以表示为：

\[\frac{BC}{OC} = \frac{MK}{OK} = \frac{ED}{OD} \]

\(BC\)表示了点\(B\) 到图像平面中心\(C\)的距离，并且在正交化图像坐标系中，\(OC\) = 1，在这个条件下，\(MK\)可以表示为

\[MK = \frac{BC \times OK}{OC} = \sqrt{x_u^2 + y_u^2} \times h \]

\(IA\)表示从点\(I\)到\(XY\)平面中心\(A\)的距离

\[IA = ED = \frac{BC \times OD}{OC} = \sqrt{x_u^2 + x_v^2} \times z_v \]

最后，结合以上等式，该折射模型中的“虚拟-真实”关系可以表示为：

\[\begin{cases} x_c = x_v\\ y_c = y_v\\ z_c = h + (z_v - h) \times \sqrt{n ^ 2 + (n^2 - 1) \times (x_u^2 + y_u^2)} \end{cases} \\ where\quad x_v = z_v \times x_u, y_v = z_v \times y_u \]