扫描线学习笔记

用途

用于处理平面中矩形重叠、矩形与点相关问题，比如求矩形面积的并，周长的和，以及求一个点被多少个矩形包含等问题。

扫描线是一个离线算法，即一般用于处理多组询问的。

使用方法

本质就是把二维的矩形问题投射到一维的线段问题上。

我们先将每一个矩形拆成两条线段——上边界与下边界，标记每一条是上边界还是下边界，然后按高度排序。

依次取出每一条边界，这个过程就像一条线从上往下扫描的过程。

 

 

 

 

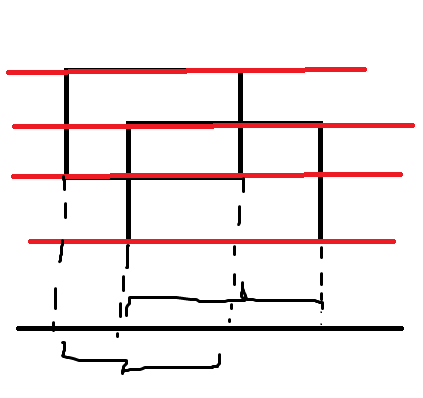
拿矩形面积并来举例，我们在这个过程中维护一个线段树，以横坐标为下标，扫到上边界时就把上边界的横坐标区间的值+1，

扫到下边界时求询问不为0的位置数量t，用t乘上高度差就得到了这一段的面积并，累计到答案中。然后将下边界这一段区间-1

如此往下扫描至没有边界位置。

如果询问的是一个点被多少个矩形包含，有q个询问。那么我们将询问按照纵坐标排序，然后将高度高于这个询问的边界一次加入线段树/树状数组中，然后点的横坐标处的值即是该点的答案。

复杂度$O(nlogn)$

其实这个也可以用二维树状数组做，但复杂度会多一个log