哈夫曼树学习笔记

是什么

哈夫曼树是一种用于压缩字符串的算法。

就是计算出文本中每个字符/单词的出现次数，然后给每个字符/单词赋予一个二进制编码，以达到压缩的效果。

怎么做

将字符按出现次数排序丢进队里，每次取出最小的两个，合并到一个新结点上，合并的节点的出现次数就是儿子出现次数的和，然后将合并的节点丢回堆里，重复至只剩一个节点为止。

这个合并的过程是一个树形结构，在合并的时候我们顺便从新构造的节点像被合并的节点连边就行了。

然后从上往下，按如图方式构造即可（其实跟noip2002合并果子的构造方式很像）

 

 

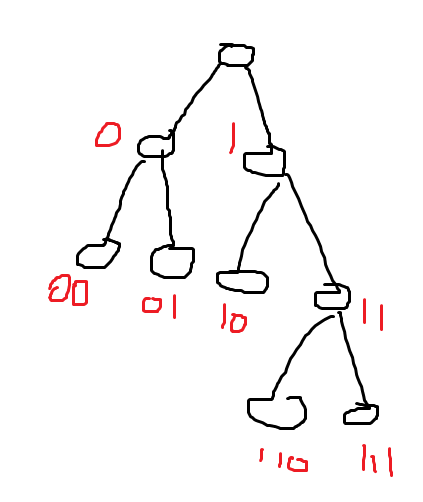
 每个叶子结点对应一个字符，这样每个字符的编码都不是任意一个字符编码的前缀，这样从左往右读取的时候就不会混淆。

如果题目要求的是k进制的话，就每次取k个节点合并，即构造k叉哈夫曼树。但这样要把字符数n补齐到【k-1的倍数+1】这样才能完美合并。（第一次k个字符，后面每次k-1个字符），用出现次数为0的字符补齐。

例题

noi2015 荷马史诗

一部《荷马史诗》中有 n 种不同的单词，从 1 到 n 进行编号。其中第 i 种单词出现的总次数为 wi。Allison 想要用 k 进制串 si 来替换第 i 种单词，使得其满足如下要求:
对于任意的 1≤i,j≤n，i≠j，都有：si 不是 sj 的前缀。
现在 Allison 想要知道，如何选择 si，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，Allison 还想知道最长的 si 的最短长度是多少？
一个字符串被称为 k 进制字符串，当且仅当它的每个字符是 0 到 k−1 之间（包括 0 和 k−1）的整数。
字符串 Str1 被称为字符串 Str2 的前缀，当且仅当：存在 1≤t≤m，使得 Str1=Str2[1..t]。其中，m 是字符串 Str2 的长度，Str2[1..t] 表示 Str2 的前 t 个字符组成的字符串
2≤n≤100000，2≤k≤9。

题解

这题除了总长最短还要求最长编码最短，也就是树的深度最小。那么我们在构造k叉哈夫曼树时排序加多一个第二关键字——该节点的深度即可。初始为0，每合并一次加1。

最后算总长度有一个技巧，我们把长度拆成一段一段的，即对于Trie树上的每一条边考虑，它增加的是它子树中叶子结点的出现次数之和。对于一棵子树，由它的儿子到达它，需要它所有子孙节点的出现次数之和。这样只要累计每个节点的出现次数就行了

代码

#include<bits/stdc++.h>
#define int long long 
using namespace std;
#define N 1000010
struct data
{
	int val,lev,id;
	data()
	{
		val=lev=id=0;
	}
}word[N];
bool operator <(data a,data b)
{
	if(a.val!=b.val) return a.val>b.val;
	return a.lev>b.lev;
}
priority_queue<data> q;
int cnt,ans,maxlen;
signed main()
{
	int n,k;
	//freopen("1.in","r",stdin);
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&word[i].val);
	}
	if((n-1)%(k-1)) n=(k-1)*((n-1)/(k-1)+1)+1;
	for(int i=1;i<=n;i++) word[i].id=i,q.push(word[i]);
	cnt=n;
	while(!q.empty())
	{
		data t;
		/*if(q.size()<100)
			printf("%lld\n",q.size());*/
		if(q.size()==1) break;
		t.id=++cnt;
		for(int i=1;i<=k;i++)
		{
			data now=q.top();
			//if(now.lev)cout<<now.val<<" "<<now.lev<<endl;
			q.pop();
			t.lev=max(t.lev,now.lev+1);
			t.val+=now.val;
		}
		ans+=t.val;
		//cout<<t.val<<" "<<ans<<endl;
		maxlen=max(maxlen,t.lev);
		q.push(t);
	}
	//dfs(q.top().id,0);
	printf("%lld %lld",ans,maxlen);
}