反演归纳总结（莫比乌斯反演，二项式反演，单位根反演）

莫比乌斯反演相关

整除分块

用于计算$\sum_{i=1}^n f(\lfloor{n/i} \rfloor)*i$之类的函数

整除的话其实很多函数值是一样的，对于每一块一样的商集中处理即可

若一个商的左边界为l,则右边界为$\lfloor{\frac{n}{\lfloor\frac{n}{l}\rfloor}}\rfloor$

这样时间复杂度就是$O(\sqrt{n})$

如果是类似$\sum_{i=1}^n f(\lfloor{n/i} \rfloor)*i \ opt \ f(\lfloor{m/i} \rfloor)$

就让r=$min(\lfloor{\frac{n}{\lfloor\frac{n}{l}\rfloor}}\rfloor,\lfloor{\frac{m}{\lfloor\frac{m}{l}\rfloor}}\rfloor)$

这样的话记得另$l<=min(n,m)$，否则会出现除以0的情况

莫比乌斯函数

如果n的因数中没有平方数，则$\mu n=(-1)^k$，k为n质因数的个数

否则$\mu n=0$

特别的，$\mu 1=1$

这样就可以得到一个性质：一个数所有因数的$\mu$之和等于0，除非这个数是1

证明：设m有n个质因数，则原式$=1-C_n^1+C_n^2-C_n^3...C_n^n$

结合二项式定理：原式$=(1-1)^n=0$，证毕

这个性质很常用，比如$[gcd(i,j)]=1$这类式子可以转化成$\sum_{d|gcd(i,j)} \mu(d)$

莫比乌斯反演

若$F(x)=\sum_{d|x} f(x)$

那么$f(x)=\sum_{d|x} F(d)*\mu(x/d)$

但一般而言用的更多的是莫比乌斯函数的性质

单位根反演

用于变形[a|x]之类的式子

单位根：就是fft的那个东西，n次单位根w就是满足$w^n=1$的w

n次单位根一定有n个，记为$w_n^0,w_n^1,...,w_n^{n-1}$

但是一般题目都是在取模的条件下进行的，所以我们一般不用复数，用原根，

即$w_n^i=g^{(p-1)/n*i}$，这样刚好有n个无不相同的原根

结论：$[a|x]=\frac{1}{a}\sum_{i=0}^{a-1}w_a^{ix}$

证明：若x是a的倍数，那么$w_a^{ix}$是$w_a^{a}$的倍数，即等于1

如果不是，可以用等比数列求和

原式可化为：$[a|x]=\frac{1}{a}\frac{w_a^{ax}-1}{w_a^x-1}$

$[a|x]=\frac{1}{a}\frac{1-1}{w_a^x-1}=0$

二项式反演

结论

如果$f(x)=\sum_{i=0}^x(-1)^i*(_i^x)*g(i)$（式子1）

那么$g(x)=\sum_{i=0}^x(-1)^i*(_i^x)*f(i)$（式子2）

可以这么理解：

（PS：补集的交集即为【【原集的并集】的补集】）

如果令$g(x)=\frac{h(x)}{(-1)^x}$

那么式子1:

$f(x)=\sum_{i=0}^x*(_i^x)*h(i)$

式子2:

$\frac{h(x)}{(-1)^x}=\sum_{i=0}^x(-1)^i*(_i^x)*f(i)$

即

$h(x)=\sum_{i=0}^x(-1)^{i+x}*(_i^x)*f(i)$

更一般的，还有（即无需从0开始）

$(-1)^{i+n}与$(-1)^{i-n}$可视作等价的

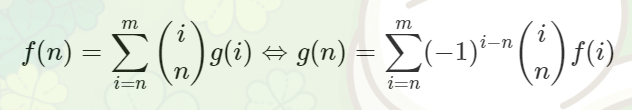
 这两条常用于构造容斥系数