[csp2020] 函数调用

前言

考试时想着用每个点map维护加法操作，然后启发式合并乱搞，然而复杂度有两个log，而且这是个DAG...

最后打了暴力滚粗

题目

https://www.luogu.com.cn/problem/P7077

题解

首先我们可以建一个0号点，向序列中的所有函数结点连边，这样就变成了调用一次0函数后的状态

考虑把加法和乘法分开来，

假设原来是$a_1+2 ,\ all*3$这样的操作，可以变为$all*3 ,\ a_1+6$

即，如果一个加法操作后面有乘法，相当于这个加法会被执行乘数次

即对于序列每一项，它的最终结果是$a_i*x+add_i$，x是全局乘上的数

考虑如何计算每一项加法操作的执行次数

因为只有后面的乘法会影响到当前的加法，所以倒序遍历子节点

对于这样一个图

 

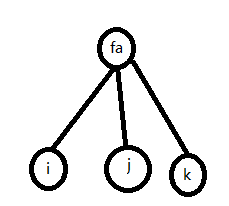
i的执行次数为【fa的执行次数】*【执行j后全局会多乘上多少】*【执行k后全局会多乘上多少】

我们可以在遍历子节点时维护一个变量multiply,表示已遍历的子节点对全局乘法的贡献

每遍历完一个，就将multiply乘上它对全局乘法的贡献，这个可以用一个dfs预处理出来

另外，由于这是个DAG,所以一个函数节点必须入读为0时才能得出最终计算次数，所以我们可以用拓扑排序这整张图

另外，对于入读为0，但不会调用的，也要将其放入初始队列

否则有些点入边消不完，导致无法进入。

 

 另外，注意乘数和加数有可能为0.

代码

#include<iostream>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
#define N 1000010
#define int long long
#define mod 998244353
int type[N],p1[N],p2[N],val[N],n,deg[N],m,vis[N];
int add[N]/*每一个位置的增加量*/,mul[N]/*调用这个函数后全局乘上的值*/,times[N]/*每个函数的调用次数*/;
vector<int> vec[N];
void dfs(int id)//计算mul
{
	mul[id]=1;
	vis[id]=1;
	//cout<<id<<endl;
	if(type[id]!=3)
	{
		if(type[id]==2)  mul[id]=p1[id];
		return;
	}
	for(int i=0;i<vec[id].size();i++)
	{
		int to=vec[id][i];
		if(!vis[to]) dfs(to);
		mul[id]*=mul[to],mul[id]%=mod;
	}
}
void topic() 
{
	queue<int> q;
	times[0]=1;
	for(int i=0;i<=m;i++) if(!deg[i])  q.push(i);
	while(!q.empty())
	{
		int now=q.front();
		q.pop();
		int multiply=times[now];//下一个调用的函数的调用次数 
		for(int i=vec[now].size()-1;i>=0;i--)
		{
			int to=vec[now][i];
			if(--deg[to]==0) q.push(to);
			times[to]+=multiply,times[to]%=mod;
			if(type[to]==1) add[p1[to]]+=p2[to]*multiply%mod,add[p1[to]]%=mod;
			multiply*=mul[to],multiply%=mod;
		}
	}
}
signed main()
{
	//freopen("call.in","r",stdin);
	//freopen("call.out","w",stdout);
	cin>>n;
	for(int i=1;i<=n;i++) 
	{
		scanf("%lld",&val[i]);
	}
	cin>>m;
	for(int i=1;i<=m;i++)
	{
		int t;
		scanf("%lld",&t);
		type[i]=t;
		if(t==1)
		{
			scanf("%lld%lld",&p1[i],&p2[i]);
		}
		else if(t==2)
		{
			scanf("%lld",&p1[i]);
		}
		else
		{
			int c;
			scanf("%lld",&c);
			for(int j=1;j<=c;j++)
			{
				int a;
				scanf("%lld",&a);
				vec[i].push_back(a);
				deg[a]++;
			}
		}
	}
	int q;
	cin>>q;
	for(int i=1;i<=q;i++)
	{
		int a;
		scanf("%lld",&a);
		vec[0].push_back(a);
		deg[a]++;
	}
	type[0]=3;
	dfs(0);
	topic();
	for(int i=1;i<=n;i++) printf("%lld ",(val[i]*mul[0]%mod+add[i])%mod);
}