OI做题方法总结
前言
永远记住:是根据思路来想需要的算法。而不是用思路来契合算法。
调不出来时多造几组样例,以躺平、无所谓的心态去调
可以通过思考部分分来取得正解,比如菊花图、链图。
不要随便开long long,常数大
考试时注意时间分配
树论的题,不是数据结构要么dp要么推结论贪心
看完题目先模拟一下样例,能摸出很多性质
找出有用的性质这题就成功了一半了。
还有就是要把算法/数据结构看作手中的工具,灵活运用,改造,堆叠在一起使用
一般一道题就四种切入口
- 直接做
- 考虑题目是否有单调性或贪心性
- 用数据结构来加速模拟过程或是维护修改等
- 数型结合?转化成图或树结构?
dp:记得写初始值,清空数组,想清楚枚举边界和递推式的使用条件,这对答案的正确性影响很大
数组:线段树开4倍,双向边开2倍,要动态开点或者可持久化的能开多大开多大。
树
常用方法:
- 贪心
- 树形dp
- 重链剖分
- 长链剖分(多用于优化dp)
- 点分治(联通块有关问题,比如求树中指定距离的点对个数)
- 树上莫队(如果要求路径信息考虑用欧拉序列,即每个点dfs开始和结束都放入序列内,并标记是进入还是退出)
注意点分治的过程中要维护一个isroot[i]数组,标记i是否曾今当过重心,getroot,divide,getdep函数碰到isroot[to]=true的点都要避开(否则等着TLE吧)
注意树形背包的复杂度是$nV$的
树形dp的思考方式一般是
考虑叶子向其父亲的贡献(一片两片三片地递增地考虑)
然后再逐层往上考虑,总结性质
如果题目中有操作之类的,考虑树链剖分维护
树链剖分的懒标记有两种,一种在线段树上推,一种直接通过树上推。
询问路径的最值或方案数之类的,考虑用路径拼接,有两种常见方法
- 树形dp,开一个维度标记已经决定了多少个端点
- 每一个点从儿子那继承一堆这个点为起点,终点在子树内的路径,然后拼接
一些方法&结论:
如果有奇偶等限制,考虑黑白染色
对于既有边权又有点权的图,考虑把它们集中于点上
树上维护信息的题,考虑启发式合并(二维树形dp或维护方案)
按大小分轻重儿子:重链剖分
按长短分轻重儿子:长链剖分
换根操作:可以用分类讨论避免换根导致的子树信息重置。
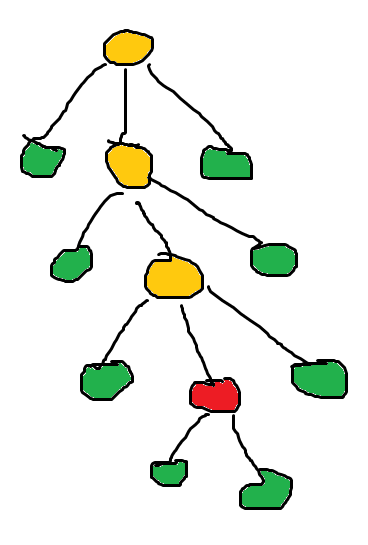
比如上面这张图,原本的根是最高的那个。
现在要把红色的点换为根。
那么原图只有新根的祖先会收到影响。即,他们的子树变为了整棵树除去【它到新根的那个儿子的子树】 。
这样它的子树的区间会被拆成一个前缀区间一个后缀区间。可以考虑将dfn序列倍长,将前缀拼到后缀后面去。
其他绿色点的子树信息均不受影响。
遇到求指定范围森林里树的个数,即在全部是树的环境中求联通块个数,考虑如下结论:树的个数=点数-边树。
树的重心一定在从根节点出发的重链上,故除dp外我们还可以从根节点出发沿重链前进,遇到第一个点满足父亲那一块面积小于总大小的一半。(CSP-S d2t3)
在树上求经过一些点的最短路径,这条路径等于这些点的最小生成树的两倍,且一定是按照这些点的dfs序依次经过([SDOI2015]寻宝游戏)
图
图的核心思维就是把图问题转化为树问题求解
图的常用方法不多,大概就以下几种
- tarjan
- 最短/长路
- 最小/大生成树
- 并查集
如果有限定恰好几步或是多层结构一样的图,考虑矩阵快速幂优化(把邻接矩阵相乘k次就是走了k步后的距离矩阵)
若图论中要大规模建边,考虑线段树优化建边(【BZOJ3218】a + b Problem,[CF787D] legacy )
对于数据较小,状态二选一,求最大的且有图论背景的考虑最小割(【NOI2009】植物大战僵尸,【BZOJ2127】happiness,【BZOJ1143】【CTSC2008】祭祀)
图论dp可以点数较小时,dp层数较多时可以考虑矩阵乘法优化(「BZOJ1875」[SDOI2009] HH去散步)
有向图dp时,若可以走回头路,则情况会很复杂,考虑先缩点变成DAG,再dp
有些题目无法直接构造,可以转化为每个要求为一些限制,求这个限制系统有无解。(比如CSP-S d1t3).检查可以通过并查集、链表、拓扑排序、搜索完成。
要在一个序列的基础上生成一个排列,可以考虑转化为图论问题,从i向$a_i$处连边。
最值规划
常用方法:
- 贪心
- dp
- 二分
- 网络流(其实可以看作一种带反悔的贪心或者dp)
- 模拟退火(不会)
网络流有时可以考虑用数据结构模拟。
贪心有时可以和dp结合起来用
(其实很多方法都是通的,可以搭配起来用)
方案统计
题型:求一些满足某些限制的方案数
常见套路(也是结合起来用)
- 正反互换:用总方案数-不满足限制的方案数
- 排列组合
- 容斥(有$O(n)$和$O(2^n)的$
- dp
有些题目需要去重,可以考虑重复的方案有什么共同的性质,再体现在代码中。
如果要求的是恰好有k个满足的情况数,但只能求出至多或至少的情况数,考虑组合容斥。
一些优化
dp
先考虑最朴素的dp方式
然后再考虑优化
但是要注意正确性
- 删减状态:一些意义相近的状态或许可以合并,或者可以用一些性质省略掉的,比如差分等操作(emiya家今天的饭)
- 数据结构优化:单调队列,斜率优化,线段树/树状数组,堆等
同构dp方程优化:
对于每一个位置的dp方程都一样,没有判断句等东西影响,可采取这种优化。
- f[i][j],i很大,j在n^3范围内,矩阵快速幂
- f[i][j],i在n^2范围内,j很大,且转移方程没有min,max之类的东西:拉格朗日插值,盲猜次数<=n
- 也可以考虑是否能交换i,j的枚举顺序
概率dp,有可能递推到后面概率变化很小,这样就不需要推完整个n。
序列维护相关
这种题就应该上大数据结构来搞
维护颜色数、mex考虑莫队、主席树、分块,也可以考虑维护一个pre[i]数组表示上一个与这个位置相同颜色的的位置(noi online t2)
计算一堆区间函数,一个一个函数统计是比较低效的,可以从贡献的角度考虑
在线
- 线段树/树状数组
- 平衡树(节点并不一定代表一个位置,也可以代表一段区间)
- 分块
- 倍增
- 树链剖分(树中路径的维护)
- 点分治(树中指定距离内区块的维护)
- lct(带删连边操作的)
离线
- 莫队
- 整体二分
- cdq
有个套路就是维护区间min,max,相当于在操作区间内找出一个分割点分开处理
有些区间推平操作可以用维护min,max的方式来维护
区间整数除法可以维护min,max,然后看作区间减法来处理
若要求序列中每个点的left[i]和right[i],即左边和右边距离它最近的且比它大\小的点,用单调队列两边各跑一次即可
求最长上升\下降子序列可以用树状数组做到nlogn,即正序枚举对于已经计算完的j,把dp[j]插到树状数组中的val[j]处。val[j]为第j位的权值,计算dp[i]=树状数组中[1,val[i]-1]区间的最大dp值+1,然后再把dp[i]插入。这样需要对权值进行离散化。
bzoj一个简单的询问:求两段区间权值相同的位置的对数,可以将其拆成四个前缀询问用莫队处理,具体请百度。
其他
除了遍历外,可以用dp初始化数组
bool开桶开不下可以考虑bitset
O(1)统计一个数二进制位的一的个数:先预处理$2^{16}$以内的数的答案,然后将目标数不断除与$2^{16}$
期望具有可加性,即两个随机变量的和的期望等于两个随机变量的期望的和,即$E(X+Y)=E(X)+E(Y)$


