【ARC083E】Bichrome Tree

题目

有一颗N个节点的树，其中1号节点是整棵树的根节点，而对于第ii个点(2≤i≤N)，其父节点为PiPi

对于这棵树上每一个节点Snuke将会钦定一种颜色（黑或白），以及一个非负整数的点权。

Snuke有一个他最喜欢的整数序列，X1,X2,...,XN，他希望能够钦定这些点的点权和颜色。使得:

对于每一个点i，都满足i的整颗子数内所有和i颜色相同的点(包括ii本身)的点权和恰好为Xi。

现在给定你这棵树的结构和Snuke最喜欢的整数序列，请你判断是否有一种钦定的方案使得其满足上文所述的条件

$n<=1000 x_i<=5000$

题解

考虑自底向上树形dp

叶子节点的话无论是黑是白点权都是$x_i$

而他的父亲可以任意选择某些点与它同色，拼出小于等于它的点权的和（剩余的部分可以有自己的点权补上）

就算每个儿子点权都比它大，也可以让所有儿子与它异色。

再往上一层就复杂一点了，因为此时就算让儿子与自己异色，它的子树中还是有可能有与自己同色的

如下图，不管是儿子是同色还是异色，都要加一些东西

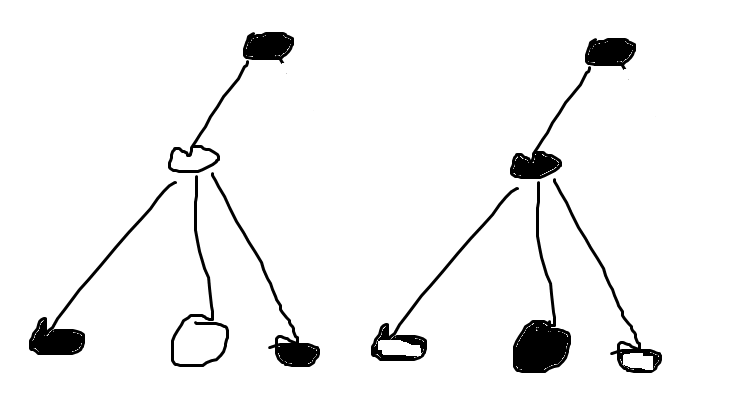
就是说，要么加上儿子的点权，要么加上儿子子树中与儿子异色的点权和

其中儿子的点权题目规定了，改不了

但异色的点权是可以改的

因为我们最重要选出点权和小于等于自己的点

所以异色的点权越小越好，这样就更加可能完成上面要求

因为总点权是固定的，所以同色的点权越小，异色的点权就越大

我们可以用类似背包的方式找出可能的最小的同色点权和，用总点权和减去它算出异色点权和并向上传递

如果凑不出小于等于自己的点权和，就代表不可能完成，直接退出

代码

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstring>
using namespace std;
#define N 5010
int val[N];
int dp[1010][N];
vector<int> vec[1010];
int dfs(int id)
{
	if(!vec[id].size()) return 0;
	int tot=0;
	for(int i=0;i<vec[id].size();i++)
	{
		int to=vec[id][i];
		int v=dfs(to);
		tot+=v+val[to];
		if(!i)
		{
			if(v<=val[id]) dp[id][v]=0;
			if(val[to]<=val[id]) dp[id][val[to]]=0;
		}
		else
		{
			for(int j=val[id];j>=0;j--)
			{
				if(j>=val[to]&&dp[id][j-val[to]]==i-1) dp[id][j]=i;//这个条件是保证每个点都选了其中一个状态
				if(j>=v&&dp[id][j-v]==i-1) dp[id][j]=i;
			}
		} 
	}
	for(int i=val[id];i>=0;i--)
	{
		if(dp[id][i]==vec[id].size()-1) return tot-i;
	}
	throw 1;
}
int main()
{
	memset(dp,-1,sizeof(dp));
	int n;
	cin>>n;
	for(int i=2;i<=n;i++)
	{
		int a;
		scanf("%d",&a);
		vec[a].push_back(i);
	}
	for(int i=1;i<=n;i++) scanf("%d",&val[i]);
	try
	{
		dfs(1);
	}
	catch(...)
	{
		cout<<"IMPOSSIBLE";
		return 0;
	}
	cout<<"POSSIBLE";
}
/*
7
1 2 2 1 5 5 
3 3 4 4 1 1 1
*/