用概率与期望分析抽卡游戏

前言

在各种游戏中，常常有抽卡这一环节，一般游戏会给出每个物品的掉落概率
但一般稀有物品概率极少，所以需要评估现有的货币是否有足够大的概率抽到卡

概率

设掉落概率为a,次数为x，设f(x)表示x次内抽到的概率（我们一般关注这个值）
考虑反向思维，用1-（x次都抽不中的概率）计算f(x)
抽不中的概率为\(1-a\)
x次就是\((1-a)^x\)
则
\(f(x)=1-(1-a)^x\)
若a取0.02
画出来大概是（为了可视化将f(x)乘了100）

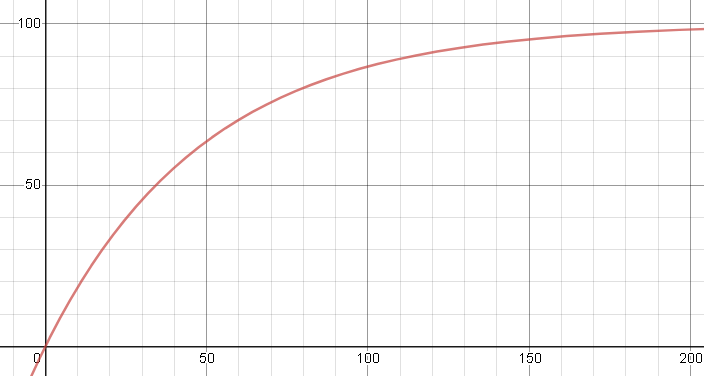
可以看出开始快速增长，然后逐渐放缓、

期望

除了概率之外，我们还会关注一般要多少次才能抽中，
第i天期望为\(g(i)=a(1-a)^i\)
则总期望为
\(\sum_{i=1}^{\infty} i*a(1-a)^i\)
如果去掉系数i,则就是一个(1-a)为公比的等比数列，考虑变成下面的式子
\(\sum_{i=1}^{\infty} \sum_{j=i}^{\infty} a(1-a)^j\)
套用求和公式
\(\sum_{i=1}^{\infty} a*(1-a)^i \ * \ \frac{1-(1-a)^{\infty}}{a}\)
消掉a
\(\sum_{i=1}^{\infty} (1-a)^i \ * \ (1-(1-a)^{\infty})\)
\((1-a)^{\infty}\)趋向于0（因为\(0<1-a<1\)）
所以右边的乘数趋向于1
原式等于
\(\sum_{i=1}^{\infty} (1-a)^i\)
这又是一个等比数列，（1-a）为公比
则原式等于\(\frac{1-(1-a)^{\infty}}{a}\)
即\(\frac{1}{a}\)
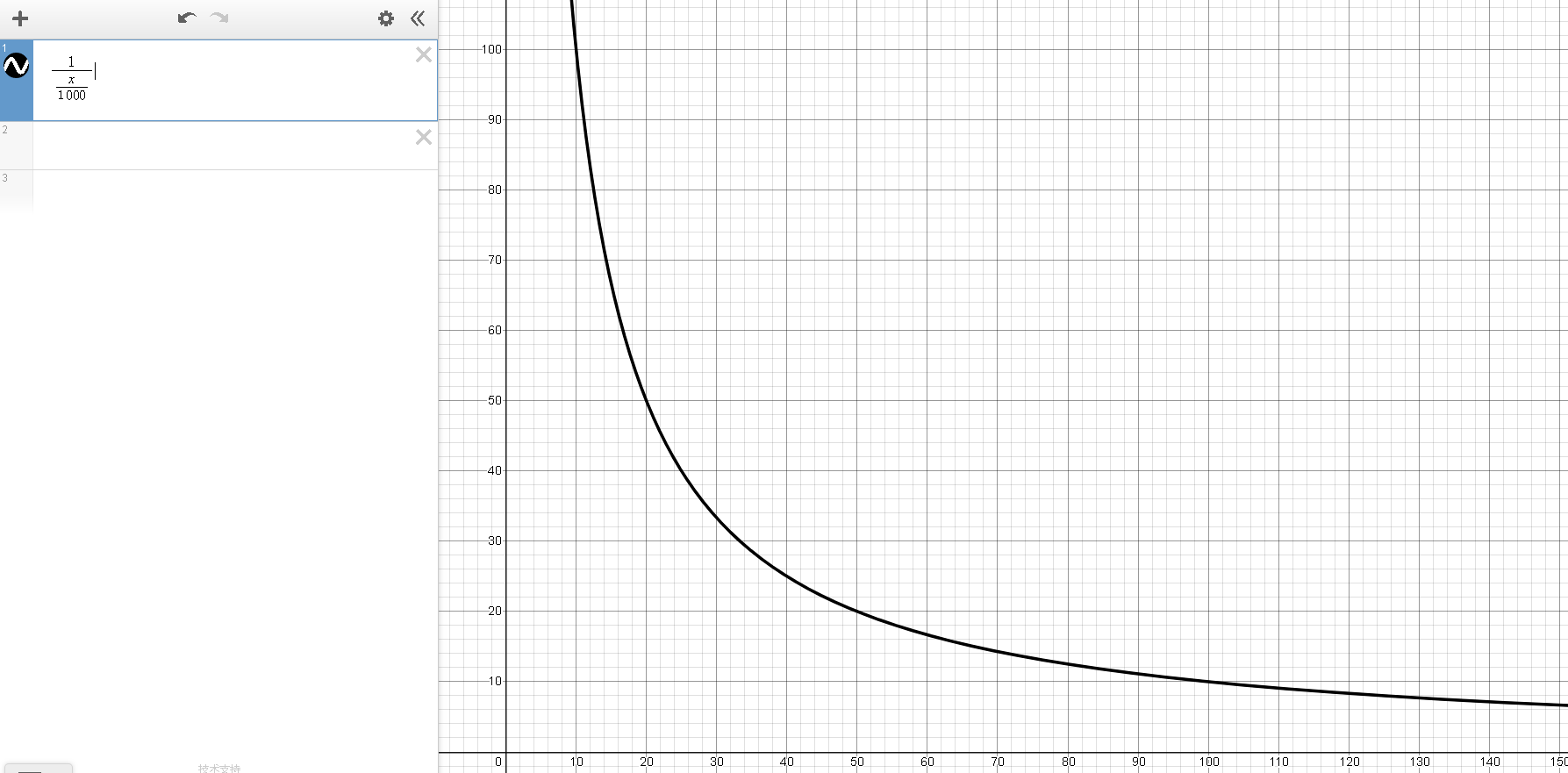
就是一个反比例函数
画出来像这样，（为了可视化放大了1000倍，即x坐标为x的对应概率为x/1000）

总结

有了这两个工具后，在抽卡时就能更理智地分析是否应该投入货币去抽，希望对大家有所帮助
update:
其实后面那个结论就是个傻逼结论，
就当是推公式玩吧
列位看官请勿见笑