[bzoj4372] 烁烁的游戏 （点分治+线段树）

题目

给一颗n个节点的树，边权均为1，初始点权均为0，m次操作：
Q x：询问x的点权。
M x d w：将树上与节点x距离不超过d的节点的点权均加上w。

$n,m<=10^5$

题解

树上的题，要联想到用树链剖分或是点分治处理。

这题先用点分治建点分树，

修改时不能暴力修改，考虑打标记，

但一个点可能有多重标记，处理起来比较复杂

其实每次修改（M x d w）对于这个点p而言，我们只需要知道d-dis(x,p)和w是多少即可。

考虑用线段树作为标记。

每个点塞一颗线段树，以子树内的点（新的树）到这个点的距离为下标，修改时将$[0,d-dis(x,p)]$区间增加w即可

每次修改时就一路往上更新

这样时空复杂度是$O(n*log_n^2)$的

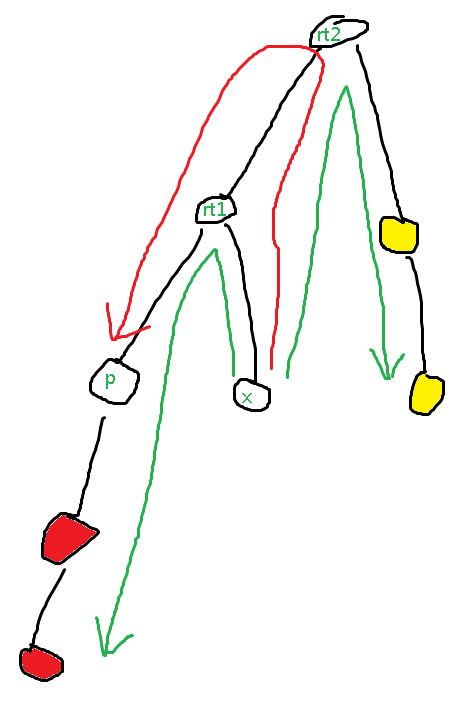
另外，注意下图，假设现在是 (M,x,4,w)，

那么在rt1处可以访问到p点和红色点，在rt2处可以访问到p点和黄色点，

这样若是查询时经过p点，那么会减两次w

所以我们要在rt1处更新时将p点排除在外

具体的话就是在原基础上将$ [0,d-dis(rt2,x)-dis(rt1,rt2)]$减去w

 

 

为了节省时间，我们可以标记永久化

查询时就从那个点开始一路向上，累加一路的标记。

代码

#include <iostream>
#include <cstdio>
#include <vector>
#include <stack>
using namespace std;
#define N 110000

int dep[N],root,sz[N],val[25602560],sum,fa[N],up[N][20],rt1[N],rt2[N],cnt,lc[25602560],rc[25602560],n,mson[N];
bool isroot[N];
vector<int> vec[N];
void get_dep(int id,int from)
{
	dep[id]=dep[from]+1;
	up[id][0]=from;
	for(int i=1;i<20;i++) up[id][i]=up[up[id][i-1]][i-1];
	if(id==43244)
		int asfd=0;
	for(int i=0;i<vec[id].size();i++)
	{
		int to=vec[id][i];
		if(to==from) continue;
		get_dep(to,id);
	}
}
int get_dis(int a,int b)
{
	if(dep[a]<dep[b]) swap(a,b);
	int tot=0;
	for(int i=19;i>=0;i--) if(dep[up[a][i]]>=dep[b]) a=up[a][i],tot+=(1<<i);
	if(a==b) return tot;
	for(int i=19;i>=0;i--) if(up[a][i]!=up[b][i]) a=up[a][i],b=up[b][i],tot+=(1<<(i+1));
	return tot+2;
}
void getroot(int id,int from)
{
    sz[id]=1;
    mson[id]=0;
    for(int i=0;i<vec[id].size();i++)
    {
        int to=vec[id][i];
        if(isroot[to]||to==from)continue;
        getroot(to,id);
        sz[id]+=sz[to];
        mson[id]=max(mson[id],sz[to]);
    }
    mson[id]=max(mson[id],sum-sz[id]);
    if(mson[id]<mson[root])
    {
        root=id;
    }
}
void build(int id)
{
    isroot[id]=true;
    for(int i=0;i<vec[id].size();i++)
    {
        int to=vec[id][i];
        if(isroot[to])continue;
        sum=sz[to];
        if(id==922)
        {
        	int al=1;
		}
		root=0;
        getroot(to,id);
        fa[root]=id;
        build(root);
    }  
}
#define mid (l+r)/2
void change(int &id,int l,int r,int tl,int tr,int v)
{
	if(tr==14347&&v==1895)
		int asfs=0;
	if(!id)
	{
		id=++cnt;
		//if(cnt>200000) throw 1;
	}
	if(l>=tl&&r<=tr)
	{
		val[id]+=v;
		return;
	}
	if(tl<=mid) change(lc[id],l,mid,tl,tr,v);
	if(tr>mid) change(rc[id],mid+1,r,tl,tr,v);
}
void modify(int id,int dep,int v)
{
	int t=id;
	change(rt1[t],1,n,1,dep+1,v);
	while(fa[t])
	{
		int d=get_dis(fa[t],id);
		if(d>dep) goto jump;
		change(rt2[t],1,n,1,dep-d+1,v);
		change(rt1[fa[t]],1,n,1,dep-d+1,v);
		jump:t=fa[t];
	}
}
int query2(int id,int l,int r,int pos)
{
	if(!id) return 0;
	if(l==r) return val[id];
	if(pos<=mid) return val[id]+query2(lc[id],l,mid,pos);
	return val[id]+query2(rc[id],mid+1,r,pos);
}
int query(int id)
{
	int t=id;
	int ans=query2(rt1[t],1,n,1);
	while(fa[t])
	{
		int d=get_dis(fa[t],id);
		ans+=query2(rt1[fa[t]],1,n,d+1)-query2(rt2[t],1,n,d+1);
		t=fa[t];
	}
	return ans;
}
signed main()
{
	int m;
	freopen("4372/1.in","r",stdin);
	freopen("out.txt","w",stdout);
	cin>>n>>m;
	mson[0]=1e9;
	for(int i=1;i<n;i++)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		vec[a].push_back(b);
		vec[b].push_back(a);
	}
	get_dep(1,0);
	sum=n;
	getroot(1,0);
	build(root);
	for(int i=1;i<=m;i++)
	{
		char ch;
		int a,b,c;
		scanf(" %c%d",&ch,&a);
		//cout<<ch<<" "<<a;
		if(ch=='Q') printf("%d\n", query(a));//,cout<<endl;
		else
		{
			scanf("%d%d",&b,&c);
		//	cout<<" "<<b<<" "<<c<<endl;
			modify(a,b,c);
		}
	}
}