【BZOJ1565】【NOI2009】植物大战僵尸

前言

纪念一下：网络流专题第一道自己想出来的题！(即，跟题解可能有所不同，但应该是能过的

题意

一个n*m的网格，每个网格有一个攻击位置集合，可以秒杀僵尸，僵尸从右往左进攻，吃掉一个植物可获得能量值（可能为负），求最大能量值

题解

首先每个植物可以选择吃或不吃，这种从两个状态中选一个，选择之间互相影响，求最优解的题可以考虑dp或最小割。

于是每个点分别与源点和汇点连边，若割掉源点的连边就表示吃了它，若割掉汇点的连边就表示不吃它，最终用能量和减去最小割（即损失的能量）

因为有些能量为负，于是把所有边的容量+=一个基础值base

于是到汇点的容量为$power[i]+base$,到源点容量为$base$

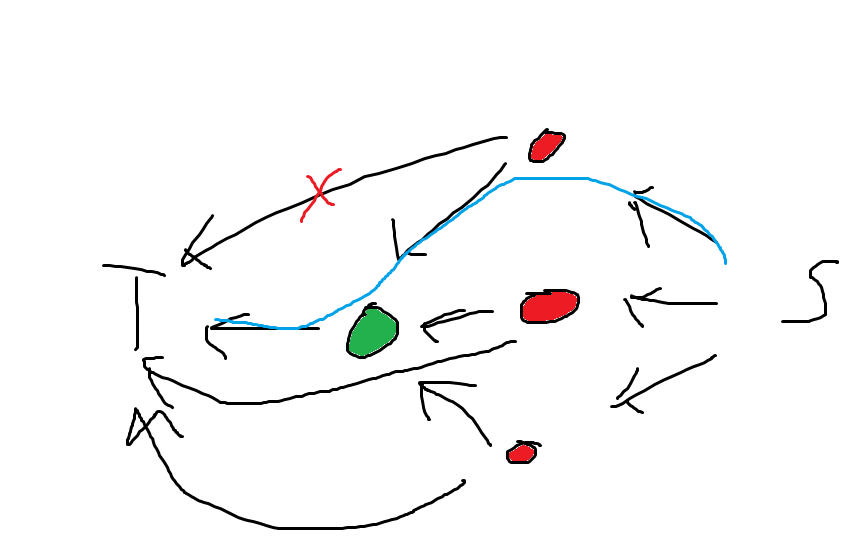
然后每个植物向它保护的植物连边（包括它后面的），容量为inf（即不可割），效果如下图，红色是绿色的保护植物。

这样若是不吃任何一个红色植物（割开它与T的连边），就会出现如图蓝色的联通路径（此时不可割开s到红色点的路径），只能连带地不吃绿色的植物

这样就保证了吃一个植物时必须先把保护它的植物都吃了

最终样例建出来的图就长这样

 

 

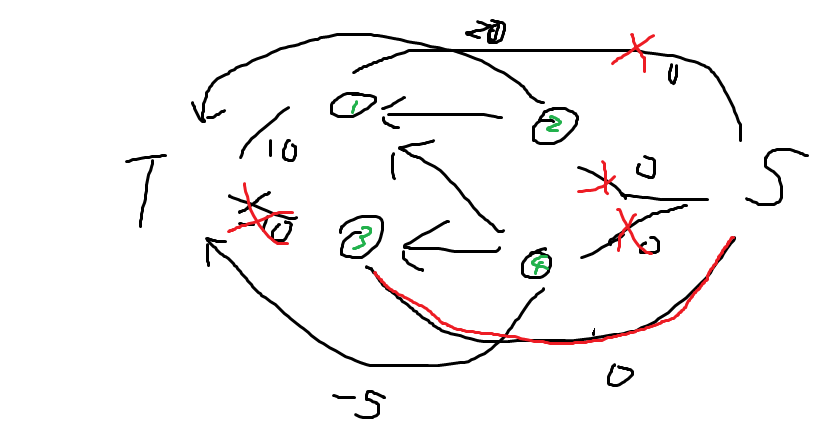
 求得的最小割要减去【割边的数量】*base

具体的话可以在残余流量里从s开始dfs

凡事能从s开始能流到的点标记为1，其他的标记为0，起点为1终点为0的非反向边边集是一组最小割边集。

void get_tag(int id)
{
	tag[id]=true;
	for(int i=head[id];i;i=nxt[i])
	{
		if(!cap[i]||tag[to[i]]) continue;
		get_tag(to[i]);
	}
}

　　在main中

int flow=dicnic(inf);
get_tag(st);
for(int i=1;i<=cnt;i++)
{
	if(tag[from[i]]^tag[to[i]]&&!cap[i]&&(i&1)) 
	{
		flow-=base;
		//printf("%lld -> %lld\n",from[i],to[i]);
	}
}

　　

注意有可能出现两个植物互相保护的情况，可以用拓扑排序去除

void topic()
{
	queue<int> q;
	for(int i=1;i<=n;i++) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int now=q.front();
		q.pop();
		for(int i=0;i<vec[now].size();i++)
		{
			int t=vec[now][i];
			add(now,t,-1);
			if(!in[t]) q.push(t);
		}
	}
	for(int i=1;i<=n;i++) if(in[i]) ban[i]=true;//标记无法进攻的植物
}

　在main中

int tot=0,n1,m;
cin>>n1>>m;
n=n1*m;
for(int i=0;i<n1;i++)
{
	for(int j=0;j<m;j++)
	{
		int t;
		scanf("%lld%lld",&power[pos(i,j)],&t);
		for(int k=1;k<=t;k++)
		{
			int x,y;
			scanf("%lld%lld",&x,&y);
			vec[pos(i,j)].push_back(pos(x,y));
			add(pos(i,j),pos(x,y),1)
		}
		if(j) vec[pos(i,j)].push_back(pos(i,j-1)),add(pos(i,j),pos(i,j-1),1);
	}
}
topic();
for(int i=1;i<=n;i++)
{
	if(ban[i]) continue;
	for(int j=0;j<vec[i].size();j++)
	{
		int t=vec[i][j];
		if(ban[t]) continue;
		connect(i,t,inf);//网络流连线函数
	}
	connect(st,i,base);
	connect(i,ed,base+power[i]);
	tot+=power[i];
}

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
#define N 1000010
#define rev(i) (((i-1)^1)+1)
#define st N-9
#define ed N-8
#define inf 0x7ffffffffff
#define base 20000
#define int long long
#define pos(i,j) (i*m+j+1)
#define add(i,j,k) out[i]+=k,in[j]+=k;
vector<int> vec[N];
int head[N],cnt,to[N],lev[N],tot,nxt[N],cap[N],power[N],in[N],out[N],from[N],n;
bool tag[N],ban[N];
void connect(int a,int b,int c)
{
	to[++cnt]=b,from[cnt]=a,cap[cnt]=c,nxt[cnt]=head[a],head[a]=cnt;
	to[++cnt]=a,from[cnt]=b,cap[cnt]=0,nxt[cnt]=head[b],head[b]=cnt;
}
bool bfs()
{
	memset(lev,0,sizeof(lev));
	queue<int> q;
	q.push(st);
	lev[st]=1;
	while(!q.empty())
	{
		int now=q.front();
		q.pop();
		for(int i=head[now];i;i=nxt[i])
		{
			if(lev[to[i]]||!cap[i]) continue;
			lev[to[i]]=lev[now]+1;
			q.push(to[i]);
		}
	}
	if(!lev[ed]) return false;
	return true;
}
int dfs(int id,int flow)
{
	if(id==ed||!flow) return flow;
	int t=flow;
	for(int i=head[id];i;i=nxt[i])
	{
		if(lev[to[i]]!=lev[id]+1||!cap[i]) continue;
		int f=dfs(to[i],min(cap[i],flow));
		flow-=f;
		cap[i]-=f;
		cap[rev(i)]+=f;
	}
	if(flow) lev[id]=0;
	return t-flow;
}
int dinic()
{
	int ans=0;
	while(bfs())
	{
		ans+=dfs(st,inf);		
	}
	return ans;
}
void topic()
{
	queue<int> q;
	for(int i=1;i<=n;i++) if(!in[i]) q.push(i);
	while(!q.empty())
	{
		int now=q.front();
		q.pop();
		for(int i=0;i<vec[now].size();i++)
		{
			int t=vec[now][i];
			add(now,t,-1);
			if(!in[t]) q.push(t);
		}
	}
	for(int i=1;i<=n;i++) if(in[i]) ban[i]=true;
}
void get_tag(int id)
{
	tag[id]=true;
	for(int i=head[id];i;i=nxt[i])
	{
		if(!cap[i]||tag[to[i]]) continue;
		get_tag(to[i]);
	}
}
signed main()
{
	int tot=0,n1,m;
	//freopen("6.in","r",stdin);
	cin>>n1>>m;
	n=n1*m;
	for(int i=0;i<n1;i++)
	{
		for(int j=0;j<m;j++)
		{
			int t;
			scanf("%lld%lld",&power[pos(i,j)],&t);
			for(int k=1;k<=t;k++)
			{
				int x,y;
				scanf("%lld%lld",&x,&y);
				vec[pos(i,j)].push_back(pos(x,y));
				add(pos(i,j),pos(x,y),1)
			}
			if(j) vec[pos(i,j)].push_back(pos(i,j-1)),add(pos(i,j),pos(i,j-1),1);
		}
	}
	topic();
	for(int i=1;i<=n;i++)
	{
		if(ban[i]) continue;
		for(int j=0;j<vec[i].size();j++)
		{
			int t=vec[i][j];
			if(ban[t]) continue;
			connect(i,t,inf);
		}
		connect(st,i,base);
		connect(i,ed,base+power[i]);
		tot+=power[i];
	}
	int flow=dinic();
	get_tag(st);
	for(int i=1;i<=cnt;i++)
	{
		if(tag[from[i]]^tag[to[i]]&&!cap[i]&&(i&1)) 
		{
			flow-=base;
			//printf("%lld -> %lld\n",from[i],to[i]);
		}
	}
	printf("%lld",tot-flow);
}