[USACO] Sprinklers 2: Return of the Alfalfa

题目

Farmer John 有一块大小为 $n*n$的网格形土地, 他想要在这片土地上种植甜玉米和紫苜蓿（mù xu），所以他需要安装一些特别的洒水器。 一个甜玉米洒水器（A）会为所有在左下角方向的格子洒水。 一个紫苜蓿洒水器(B）会为所有在右上角方向的格子洒水。 如果一个格子被一个或多个甜玉米洒水器喷洒到，那么它就能够种植甜玉米；如果一个格子被一个或多个紫苜蓿洒水器喷洒到，那么它就能够种植紫苜蓿。但是如果一个格子被两种洒水器都喷洒到了（或都没喷洒到），那么它就什么都种不了。 请你帮助 FJ 计算安装洒水器的方案数（对 $10^9+7$取模），满足每个格子最多安装一个洒水器，且每个格子都能种植（也就是说，每个格子恰好被一种洒水器喷洒到）。 有些格子已经被毛乎乎的奶牛占据了，导致这些格子上不能放置洒水器，但不影响格子能否种植植物。

题解

初步思考

首先可以发现两种洒水器的覆盖边界是一条从上面或左边开始的只能往下或往右的折线，并且两个覆盖区是完全贴合在一起的。

进一步发现只有折线的拐角处需要放洒水器，其他地方随意。

 这样就变成一个轮廓dp了。

因为两个轮廓是贴合的所以我们dp玉米的轮廓

设$dp[i][j]$表示轮廓到了$(i,j)$

它可能从$(i,j-1) or (i-1,j)$来

但这样就处理不了拐角的情况

所以每个格子加一个属性来表示这个格子从哪个方向来，三个状态如下图

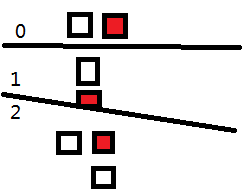
对于可填可不填的格子我们在每一个0（横着走），2（拐角）的格子处理当前那一列，具体来说就是$2^{n-cow[j]}$其中$cow[j]$表示第j列的奶牛数量，可以预处理出来。

对于0,1，这一个放不放无所谓，对于3，这一格必须放。

还需要注意

 

 

 这种拐角必须得放一个B种喷水器

转移方程

然后就可以愉快地列方程了,这里我用$map[i][j]$表示$(i,j)$有没有奶牛，有就是true

$dp[i][j][0]=dp[i][j-1][0]*2^{n-cow[j]}+dp[i][j-1][1]*2^{n-cow[j]-1}$

$dp[i][j][1]=(dp[i-1][j][1]+dp[i-1][j][2])$

$dp[i][j][2]=dp[i][j-1][0]*2^{n-cow[j]-1}+dp[i][j-1][1]*2^{n-cow[j]-1-(i>1)}$

起始状态

对于每行第一个要特殊处理,如果是0,2那上面一格必须放一个B种洒水器。方程如下

$dp[i][1][0]=2^{n-cow[1]-(i>1)}$

$dp[i][1][1]=dp[i-1][1][1]+dp[i-1][1][2]$

答案统计

从下边界和右边界统计，即从第n行的1,2格和第n列的2格统计

还有一种情况就是全图一个玉米洒水器都没有，注意在结尾加上

注意事项

不要忘取模

方程的使用条件

本题要求n^2,所以要预处理出一个记录2的次方的数组，处理到n即可。

代码

#include <iostream>
#include <cstdio>
using namespace std;
#define N 2010
#define int long long
#define mod 1000000007
int cow[N],dp[N][N][3],arr[N],pow2[N];
bool map[N][N];
int pow(int b)
{
	return pow2[b];
}
signed main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) 
	{
		for(int j=1;j<=n;j++) 
		{
			char ch;
			scanf(" %c",&ch);
			map[i][j]=(ch=='W');
		}
	}
	pow2[0]=1;
	for(int i=1;i<=n;i++) pow2[i]=pow2[i-1]*2%mod;
	for(int i=1;i<=n;i++) 
	{
		for(int j=1;j<=n;j++)  
		{
			cow[j]=cow[j]+map[i][j];
		}
	}
	arr[n+1]=1;
	for(int i=n;i>1;i--)
	{
		arr[i]=arr[i+1]*pow(n-cow[i])%mod;
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		if(!map[i-1][1])
		{
			dp[i][1][0]=pow(n-cow[1]-(i>1));
			if(!map[i][1]) dp[i][1][2]=pow(n-cow[1]-1-(i>1));			
		}
		dp[i][1][1]=(dp[i-1][1][1]+dp[i-1][1][2])%mod;
		if(i==n&&!map[i][2])
		{
			ans+=(dp[i][1][1]+dp[i][1][2])%mod*arr[3]%mod*pow(n-cow[2]-1)%mod,ans%=mod;
		}
		for(int j=2;j<=n;j++) 
		{
			dp[i][j][0]=dp[i][j-1][0]*pow(n-cow[j])%mod;
			if(!map[i-1][j]&&i>1) dp[i][j][0]+=dp[i][j-1][1]*pow(n-cow[j]-1)%mod,dp[i][j][0]%=mod;
			dp[i][j][1]=(dp[i-1][j][1]+dp[i-1][j][2])%mod;
			if(!map[i][j])
			{
				dp[i][j][2]=dp[i][j-1][0]*pow(n-cow[j]-1)%mod;
				if(!map[i-1][j]&&i>1) dp[i][j][2]+=dp[i][j-1][1]*pow(n-cow[j]-1-(i>1))%mod,dp[i][j][2]%mod;
			}
			if(i==n&&j==n&&!map[n][n]) ans+=dp[i][j][2],ans%mod;
			else if(i==n&&!map[i][j+1])
			{
				ans+=(dp[i][j][1]+dp[i][j][2])%mod*arr[j+2]%mod*pow(n-cow[j+1]-1)%mod;
				ans%=mod;
			}
			else if(j==n) ans+=dp[i][j][2],ans%=mod;
			
		}	
	}
	if(!map[n][1]) ans+=arr[2]*pow(n-cow[1]-1)%mod,ans%=mod;
	cout<<ans%mod;
}