【BZOJ1095】【ZJOI2007】捉迷藏

前言

好恶心的一道题，代码写了2.5h,调试调了5h+，局部重构了n遍。

题意

一棵树上的节点有黑白两色，初始为黑，支持修改颜色，查询最远黑点对。$n<=10^5,m<=5*10^5$

题解

ver 1

先考虑查询，可以在每个点保存一个堆s1存储子树内到这个点的路径。

再维护一个全局堆，把每个点的【最大和次大的值的和】放入堆内。

查询时直接取出堆顶。

ver 2

然后你发现你遇到了这种情况（1-2的路径被重复走了）

 

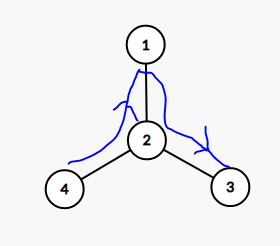
 于是在每个点再开一个新的堆s2储存它的子数内到父亲的路径。

每个点的s1从儿子的s2.top()中取得。

这样每个点只会对父亲做一次贡献（这好像是一个常见的套路）

要修改的话就从这个点开始一直往父亲走，在走的时候顺便更新（具体看代码中的on和off）

ver 3

然后你发现你的代码时空复杂度都是$O(n^2)$的

于是用点分治重构树，这样树高就是$O(logn)$，空间复杂度均摊就是$O(n*logn)$的了。

这样求距离就要用lca了，时间复杂度$O(n*logn^2)$。

注意一定要用堆，平衡树会超时（我在这调了2h+）

 

这里用到了一个小技巧：可删除任意元素的堆。

具体就是对于每个堆再维护一个堆用于存储要删除的节点。

在取top的时候看看top是否与删除堆的top相等，如相等，则删除这个top。

代码

//#pragma comment(linker, "/STACK:268435456,268435456") 
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
#define N 100010
#define int long long
class _set
{
public:
    priority_queue<int> source,del;
    int top()
    {
		while(!del.empty()&&source.top()==del.top()) source.pop(),del.pop();
		return source.top();
    }
    int size()
    {
    	return source.size()-del.size();
	}
	int sec()
    {
    	int t=top(),ret;
    	del.push(t);
    	ret=top();
    	source.push(t);
    	return ret;
	}
}s1[N],s2[N],ans;
#define _erase del.push
#define _push source.push
int to[N*2],nxt[N*2],head[N],cnt;
void connect(int a,int b)
{
    for(int i=1;i<=2;i++)
    {
		to[++cnt]=b;
        nxt[cnt]=head[a];
        head[a]=cnt;
        swap(a,b);
    }
}
int sz[N],root,used[N],fa[N],tot,up[N][21],dep[N];
void dfs(int id,int from)
{
	//printf("%d\n",id);
	up[id][0]=from;
    dep[id]=dep[from]+1;
    for(int i=1;i<=20;i++) up[id][i]=up[up[id][i-1]][i-1];
    for(int i=head[id];i;i=nxt[i]) 
    {
        if(to[i]==from) continue;
        dfs(to[i],id);
    }
}
int get_lca(int x,int y)
{
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=20;dep[x]>dep[y];i--)
    {
        if(dep[up[x][i]] >= dep[y])  x=up[x][i];
    }
    if(x==y) return x;
    for(int i=20;up[x][0]!=up[y][0];i--)
    {
        if(up[x][i]!=up[y][i])
        {
            x=up[x][i];
            y=up[y][i];
        }
    }
    return up[x][0];
}
int get_dis(int x,int y)
{
    int lca=get_lca(x,y);
    return dep[x]+dep[y]-2*dep[lca];
}
void del(_set &s)
{
    ans._erase(s.top()+s.sec());
}
void add(_set &s)
{
    ans._push(s.top()+s.sec());
}
void get_root(int id,int from,int size)
{
    sz[id]=1;
    int maxn=0;
    for(int i=head[id];i;i=nxt[i]) 
    {
        if(to[i]==from||used[to[i]]) continue;
        get_root(to[i],id,size);
        sz[id]+=sz[to[i]];
        maxn=max(maxn,sz[to[i]]);
    }
    if(max(maxn,size-sz[id])<=size/2)
		root=id;
}
void get_size(int id,int from)
{
    sz[id]=1;
    for(int i=head[id];i;i=nxt[i]) 
    {
        if(to[i]==from||used[to[i]]) continue;
        get_size(to[i],id);
        sz[id]+=sz[to[i]];
    }
}
void divide(int id)
{
    used[id]=true;
    for(int i=head[id];i;i=nxt[i]) 
    {
        if(used[to[i]]) continue;
        //puts("$");
        get_root(to[i],id,sz[to[i]]);
        fa[root]=id;
        get_size(root,0);
        divide(root);
    }
}
void off(int id)
{
    s1[id].source.push(0);//允许路径在这里停下 
    if(s1[id].size()==2) add(s1[id]);//如果之前没有添加到答案堆，则添加 
    for(int t=id;fa[t];t=fa[t])//一路往上更新父亲以及答案堆 
    {
        if(s1[fa[t]].size()>=2) del(s1[fa[t]]);//将答案堆中fa[t]旧的数据删除 
        if(s2[t].size()) s1[fa[t]].del.push(s2[t].top()); //将s1[fa[t]]中s2[t]旧的数据删除 
        s2[t]._push(get_dis(id,fa[t]));//因为现在路径可以从id开始，所以添加一条id->fa[t]的路径 
        s1[fa[t]]._push(s2[t].top());//将新的数据加入 
        if(s1[fa[t]].size()>=2) add(s1[fa[t]]);//同上 
    }
}
void on(int id)//基本同上 
{
    if(s1[id].size()==2) del(s1[id]);
    s1[id]._erase(0);
    for(int t=id;fa[t];t=fa[t])
    {
        if(s1[fa[t]].size()>=2) del(s1[fa[t]]);
        if(s2[t].size()) s1[fa[t]]._erase(s2[t].top());
        s2[t]._erase(get_dis(id,fa[t]));
        if(s2[t].size()) s1[fa[t]]._push(s2[t].top());
        if(s1[fa[t]].size()>=2) add(s1[fa[t]]);
    }
}
int sta[N];
signed main()
{
    int n,q;
    cin>>n;
    tot=n;
    for(int i=1;i<n;i++) 
    {
        int a,b;
        scanf("%d%d",&a,&b);
        connect(a,b);
    }
    dfs(1,0);
    get_root(1,0,n);
    get_size(root,0);
    divide(root);
    cin>>q;
    for(int i=1;i<=n;i++) off(i);
    for(int i=1;i<=q;i++)
    {
        char opt;
        scanf(" %c",&opt);
        int p;
        if(opt=='G') 
        {
            if(tot>=2) printf("%d\n", ans.top());
            else if(tot==1) puts("0");
            else puts("-1");
        }
        else
        {
            scanf("%d",&p);
            if(sta[p]) off(p),tot++;
            else on(p),tot--;
            sta[p]^=1;
        }
    }
}